原来动态规划如此简单！

其实动态规划就是选择和不选择的问题，将每一个所选择的最好结果记录下来，最后逐步前推最大的数就可以得到

 

该题用动态规划来写

 

 

 

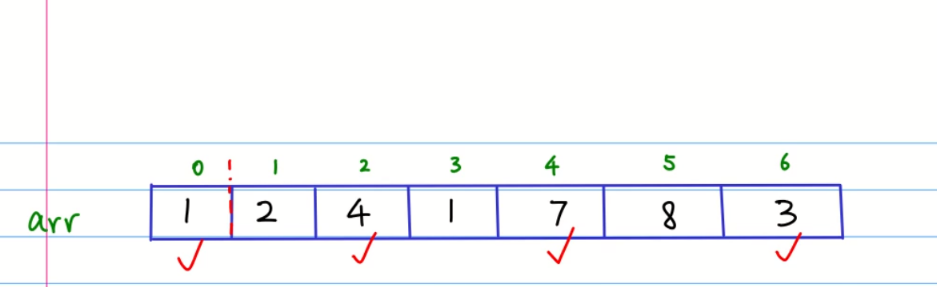
求各个不相邻的数的和，要求最大值

首先我们用递归去实现动态规划：

 

代码实现：

#include<stdio.h>
int DP(int arr[], int size);
int max(int a, int b);
int main(void)
{
    int arr[] = { 1,2,4,1,7,8,3 };
    int size = sizeof(arr) / sizeof(int);
    int sum = DP(arr, 6);
    printf("%d", sum);
    return 0;
}

int DP(int arr[], int size)
{
    if (size == 0)
        return arr[0];
    if (size == 1)
        return max(arr[0], arr[1]);
    else
        return max(arr[size] + DP(arr, size - 2), DP(arr, size - 1));
}

int max(int a, int b)
{
    if (a >= b)
        return a;
    else
        return b;
}

 但是用递归去实现会有很多问题，比如会产生很多重叠的子问题，占用的空间增加，每次的问题都需要从0和1开始计算，运算时间增加

 

所以我们可以用非递归的代码来写，用非递归代码来写就可以做到直接访问之前已经写好的最优解：

#include<stdio.h>
#include<stdlib.h>
int DP(int arr[], int size);
int good(int a, int b);
int main(void)
{
    int arr[] = { 1,2,4,1,7,8,3 };
    int size = sizeof(arr) / sizeof(int);
    int sum = DP(arr, size);
    printf("%d", sum);

    return 0;
}

int DP(int arr[],int size)
{
    int* maxnice = (int*)malloc(sizeof(int) * size);
    int A, B;
    maxnice[0] = arr[0];
    maxnice[1] = good(arr[0], arr[1]);
    for (int i = 2; i < size; i++)
    {
        A = arr[i] + maxnice[i - 2];
        B = maxnice[i - 1];
        maxnice[i] = good(A, B);
    }
    return maxnice[size - 1];
}

int good(int a, int b)
{
    if (a >= b)
        return a;
    else
        return b;
}