AC 自动机

Intention:

又是第不知道多少次被串串题破防的一天，做到最后总是认出我不会的 AC 自动机。所以！写一些我的理解（大部分来源于 OI Wiki），洗刷我被串串题恶心的耻辱。

Introduction：

前置知识：trie.

trie，即字典树，是一种字符前缀树，利用模式串串间重复的前缀，以空间换来极快的查询效率。

这棵树有一些有趣的性质：

每条边的边权都是一个字符。
从根节点出发到叶节点都是一个被插入的完整的串串。
每个节点的连向儿子的边权不会重复。

对于每一串查询的串串，时间复杂度都是 $O(\left|S\right|)$（$\left|S\right|$ 代表串串的长度）。

建树：

对于 trie，建树与其他数据结构有些不同。因为节点数量的不固定，需要动态开点。

void ins(char s[])
{
	scanf("%s",s+1);
	int len=strlen(s+1);
	int now=0;
	for(int i=1;i<=len;i++)
	{
		int x=s[i]-'a';
		if(!tr[now][x])
			tr[now][x]=++trlen;
		now=tr[now][x];
	}
}

这里的数组含义也与平时图论的存图数组不同，假设有一条从 $x$ 连向 $y$，权值为 $c$ 的边，后者是 $a_{x,y}=c$，而前者是 $a_{x,c}=y$。

这样就建好了一棵字典树了。很简单，是吧？

trie 目前只有三种用处：检索字符串、求异或最值、以及 AC 自动机。

正文：

当在一个很长的串串里面检索多个字符串的时候，朴素的做法是从每一个字符开始放到字典树上扫完整个串串。这样显然太慢了。于是 AC 自动机产生了，它可以实现扫一次目标串就可以对所有需要检索的字符串操作。

为了方便讲解，我们约定以下规则：

$G$ 代表一个已经完成插入模式串的字典树。
$S$ 代表插入字典树的模式串。
对于字典树上的每个节点，它代表一个状态 $x$，表示从根节点到该点边上所连成的字符串。显然该字符串为某几个模式串的前缀。
对于字典树上的一个节点，它的状态转移来源为节点 $fa$。
对于字典树的边，边权为 $c$。

当然不止这些规则，还有一些会在下面的定义中提及。

失配指针：

AC 自动机的精髓所在。类似于 KMP 但又有所不同，一个点的 $x$ 状态的 $fail$ 指针指向所有 $y \in G$ 中，非 $x$ 的最长后缀的状态 $y$。KMP 中的失配指针是指向最长的相同前后缀，但 $fail$ 指针指向在所有 $y \in G$ 中匹配状态 $x$ 的最长后缀的状态 $y$。虽然指向的目标不同，但功能上是一样的，都是减少串串重新匹配的时间，直接跳到最有可能匹配的地方。

构建方法：

对于一个节点，有 $trie_{fa,c}=x$。假设在字典树中所有深度比 $x$ 小的节点的 $fail$ 已求出。

如果存在 $trie_{fail_{fa},c}$，那么 $fail_x$ 指向 $trie_{fail_{fa},c}$。
否则找到 $trie[fail[fail[fa]][c]$（原谅作者突然这么写，不然真的小到看不见了），重复上一步操作。

单这么说可能很难理解，所以上图！

这是一棵插入 hers、his、she、i 的字典树（没错，我把 OI Wiki 的例子搬过来了）。我们针对 $6$ 号节点分析，图中没有边权的边即为 $fail$ 指针代表的边，并省略了其他无关节点的 $fail$ 指针。

首先找到 $fa_6=5$，看是否存在 $trie_{fail_{fa},c}$，发现 $fail_5=10$ 没有边权为 $c=\text{s}$ 的边，跳到 $10$ 号节点。
再次找到 $fa_10=0$，看是否存在 $trie_{fail_{fa},c}$，发现 $fail_10=0$ 存在边权为 $c=\text{s}$ 的边 $trie_{0,\text{s}}=7$，所以节点 $6$ 的 $fail$ 指向 $7$。

可以发现，$\text{s}$ 是 $G$ 中匹配 $\text{his}$ 的最长后缀。于是按照这样的方法，可以构建出所有节点的 $fail$。

void build()
{
	static std::deque<int>q;q.clear();
	for(int i=0;i<=26;i++)
		if(tr[0][i])
			q.push_back(tr[0][i]);
	while(q.size())
	{
		int x=q.front();q.pop_front();
		for(int i=0;i<26;i++)
			if(tr[x][i])
				fail[tr[x][i]]=tr[fail[x]][i],q.push_back(tr[x][i]);
			else//难点：！！！！！
				tr[x][i]=tr[fail[x]][i];//这里是为了其他节点以该节点作为失配指针时可以直接找到上两行中的 tr[fail[x]][i]。
				//本来是要用 while 不断寻找的，这里却用一个仿递归（就是在字典树上做一个路径压缩）的数组存下了最深的对应边
	}
}

可以看到，代码中并没有不断的跳 $fail$ 去找，而是利用了多余的空间，做了一个路径压缩。

用图可以更好的解释：

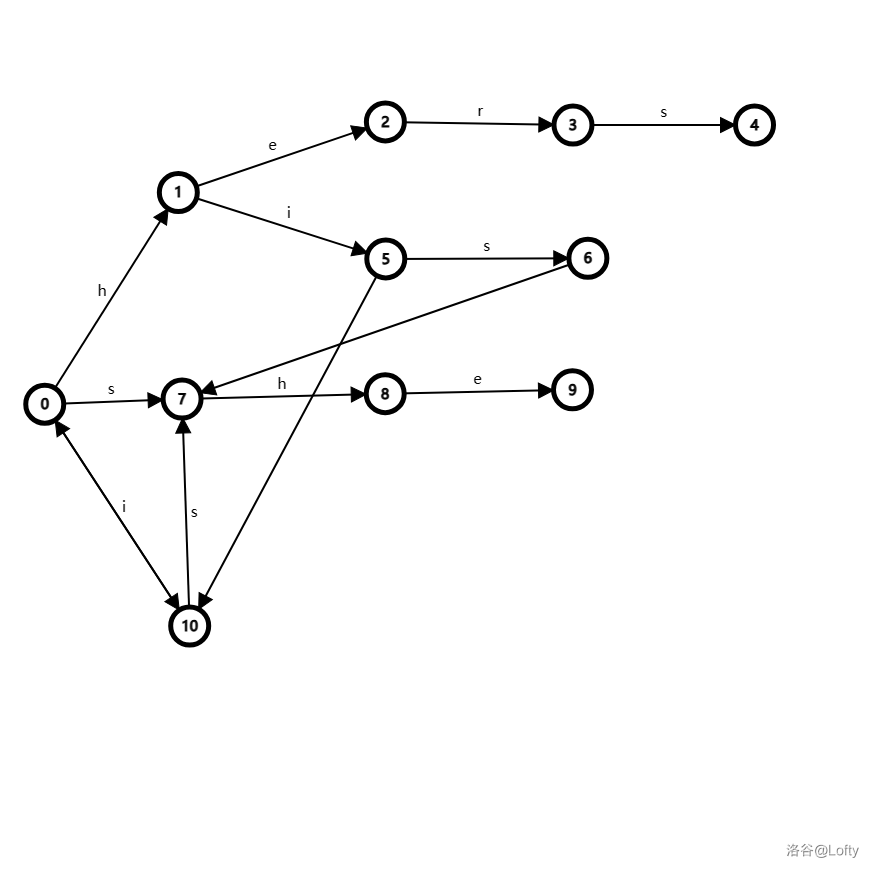
可以看到，该图相较于上一张图，多了一条 $ 10 \to 7$ 的边，并且边权为 $s$。这就是 else 里所做的事。这样，原本两步的操作 $5\to 10 \to 0$ 就只需要一步 $5 \to 10$ 即可，大大加快了效率。实质上，就是把 $10 \to 0\to 7$ 的路径压缩为 $10 \to 7$，因为是深度小的节点先压缩路径，所以在构建 $fail$ 指针时的复杂度变成了 $O(1)$，而不是并查集中不定时压缩的 $O(\log n)$，同时这还有一个作用，就是在查询时迅速找到下一个可能匹配的模式串。

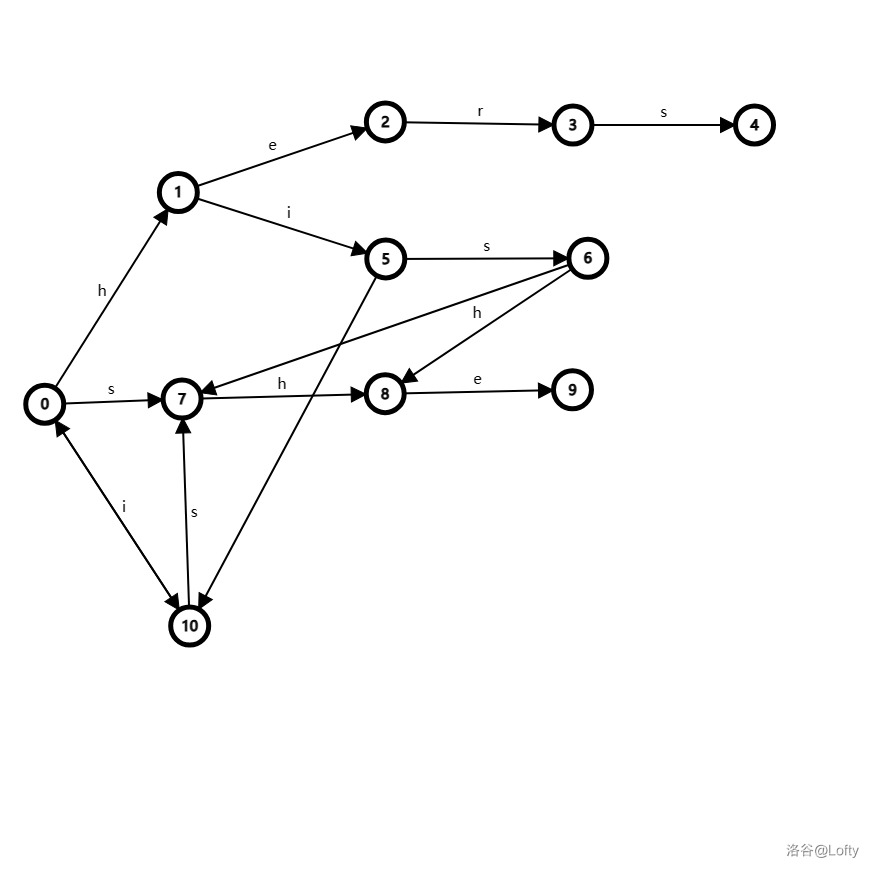
该图又新加了一条 $6 \to 8$ 的边，且边权为 $h$。因为 $fail$ 指向状态 $x$ 的最长后缀 $y$，那么在状态 $x$ 后面加一个字符（即新连的 $6 \to 8$），相当于在 $y$ 后面加了一个字符（即 $7 \to 8$），路径是等效的。所以在 hish 这种字符串中就不会落掉可能匹配的 sh 或从头开始匹配了。

查询：

最后这个就很简单了，只要顺着字典树找即可。

void query(char s[])
{
	scanf("%s",s+1);
	int now=0;
	int len=strlen(s+1);
	for(int i=1;i<=len;i++)
	{
		int x=s[i]-'a';
		now=tr[now][x];
		for(int j=now;j;j=fail[j])
			//do something...
	}
}

To be better:

但是，仍然有些毒瘤题，会卡 query 中反复跳 $fail$ 的复杂度。但也有优化手段。

观察发现，$fail$ 永远从深度更大的节点指向深度更小的节点，且每个节点仅有一个 $fail$，那么会由 $fail$ 边构成一颗树。

于是可以在 build 记录每个节点 $fail$ 的入度，在 query 中记录当前节点的操作，在最后用拓扑序统一操作即可。

void build()
{
	static std::deque<int>q;q.clear();
	for(int i=0;i<=26;i++)
		if(tr[0][i])
			q.push_back(tr[0][i]);
	while(q.size())
	{
		int x=q.front();q.pop_front();
		for(int i=0;i<26;i++)
			if(tr[x][i])
			{
				fail[tr[x][i]]=tr[fail[x]][i],q.push_back(tr[x][i]);
				++indeg[fail[tr[x][i]]];
			}
			else//难点：！！！！！
				tr[x][i]=tr[fail[x]][i];//这里是为了其他节点以该节点作为失配指针时可以直接找到上两行中的 tr[fail[x]][i]。
				//本来是要用 while 不断寻找的，这里却用一个仿递归（就是在字典树上做一个路径压缩）的数组存下了最深的对应边
	}
}
void query(char s[])
{
	scanf("%s",s+1);
	int now=0;
	int len=strlen(s+1);
	for(int i=1;i<=len;i++)
	{
		int x=s[i]-'a';
		now=tr[now][x];
			//do something...
	}
}
void topu()
{
	static std::deque<int>q;q.clear();
	for(int i=1;i<=trlen;i++)
		if(!indeg[i])
		{
			q.push_back(i);
			indeg[i]=-1;
		}
	while(q.size())
	{
		int x=q.front();q.pop_front();
		//do something...
		--indeg[fail[x]];
		if(!indeg[fail[x]])
		{
			q.push_back(fail[x]);
			indeg[fail[x]]=-1;
		}
	}
}

Code：

最后总代码奉上：

bool _Start;//😅
#define DEBUG
#include<cmath>
#include<deque>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
namespace IO
{
	#define TP template<typename T>
	#define TP_ template<typename T,typename ... T_>
	#ifdef DEBUG
	#define gc() (getchar())
	#else
	char buf[1<<20],*p1,*p2;
	#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
	#endif
	#ifdef DEBUG
	void pc(const char &c)
	{
		putchar(c);
	}
	#else
	char pbuf[1<<20],*pp=pbuf;
	inline void pc(const char &c)
	{
		if(pp-pbuf==1<<20)
			fwrite(pbuf,1,1<<20,stdout),pp=pbuf;
		*pp++=c;
	}
	struct IO{~IO(){fwrite(pbuf,1,pp-pbuf,stdout);}}_;
	#endif
	TP inline void read(T &x)
	{
		x=0;static int f;f=0;static char ch;ch=gc();
		for(;ch<'0'||ch>'9';ch=gc())ch=='-'&&(f=1);
		for(;ch>='0'&&ch<='9';ch=gc())x=(x<<1)+(x<<3)+(ch^48);
		f&&(x=-x);
	}
	TP void write(T x)
	{
		if(x<0)
			pc('-'),x=-x;
		static T sta[35],top;top=0;
		do
			sta[++top]=x%10,x/=10;
		while(x);
		while(top)
			pc(sta[top--]^48);
	}
	TP_ inline void read(T &x,T_&...y){read(x);read(y...);}
	TP void writeln(const T x){write(x);pc('\n');}
	TP void writesp(const T x){write(x);pc(' ');}
	TP_ void writeln(const T x,const T_ ...y){writesp(x);writeln(y...);}
	void writest(const std::string &a){for(int i=0;a[i];i++)pc(a[i]);}
	TP inline T max(const T &a,const T &b){return a>b?a:b;}
	TP_ inline T max(const T &a,const T_&...b){return max(a,max(b...));}
	TP inline T min(const T &a,const T &b){return a<b?a:b;}
	TP_ inline T min(const T &a,const T_&...b){return min(a,min(b...));}
	TP inline void swap(T &a,T &b){static T t;t=a;a=b;b=t;}
	TP inline T abs(const T &a){return a>0?a:-a;}
	#undef TP
	#undef TP_
}
using namespace IO;
using std::cerr;
using LL=long long;
constexpr int N=2e5+10;
constexpr int S=2e6+10;
namespace Lofty
{
	int n;
	int tr[N][30];
	int fail[N];
	int trlen;
	int indeg[N];
	void ins(char s[],int num)
	{
		scanf("%s",s+1);
		int len=strlen(s+1);
		int now=0;
		for(int i=1;i<=len;i++)
		{
			int x=s[i]-'a';
			if(!tr[now][x])
				tr[now][x]=++trlen;
			now=tr[now][x];
		}
	}
	void build()
	{
		static std::deque<int>q;q.clear();
		for(int i=0;i<=26;i++)
			if(tr[0][i])
				q.push_back(tr[0][i]);
		while(q.size())
		{
			int x=q.front();q.pop_front();
			for(int i=0;i<26;i++)
				if(tr[x][i])
				{
					fail[tr[x][i]]=tr[fail[x]][i],q.push_back(tr[x][i]);
					++indeg[fail[tr[x][i]]];
				}
				else//难点：！！！！！
					tr[x][i]=tr[fail[x]][i];//这里是为了其他节点以该节点作为失配指针时可以直接找到上两行中的 tr[fail[x]][i]。
					//本来是要用 while 不断寻找的，这里却用一个仿递归（就是在字典树上做一个路径压缩）的数组存下了最深的对应边
		}
	}
	void query(char s[])
	{
		scanf("%s",s+1);
		int now=0;
		int len=strlen(s+1);
		for(int i=1;i<=len;i++)
		{
			int x=s[i]-'a';
			now=tr[now][x];
				//do something...
		}
	}
	void topu()
	{
		static std::deque<int>q;q.clear();
		for(int i=1;i<=trlen;i++)
			if(!indeg[i])
			{
				q.push_back(i);
				indeg[i]=-1;
			}
		while(q.size())
		{
			int x=q.front();q.pop_front();
			//do something...
			--indeg[fail[x]];
			if(!indeg[fail[x]])
			{
				q.push_back(fail[x]);
				indeg[fail[x]]=-1;
			}
		}
	}
	char s[N],t[S];
	void work()
	{
		read(n);
		for(int i=1;i<=n;i++)
			ins(s,i);
		build();query(t);topu();
	}
}
bool _End;
int main()
{
	// fprintf(stderr,"%.2lf MB\n",(&_End-&_Start)/1048576.0);
	Lofty::work();
	return 0;
}
//😱

后话：

所以呢，串串题还是很恶心。

posted @ 2024-05-09 17:39 wmtl_lofty 阅读(26) 评论(0) 收藏举报

刷新页面返回顶部

lofty2007