背包DP
背包DP
0x00 0/1背包与DP的基本思路
1、定义状态
「状态」是我们在动态规划过程中数组所储存的值。一个正确的「状态」应该满足以下的要求:
-
「状态」是一个数组
-
可以通过「状态」,在完成DP后计算出答案
-
可以通过少量的公式/方程,完成不同「状态」的转移
举个例子
最基础的动态规划问题当属 0/1背包 问题,这个问题的通用描述如下:
现有 \(n\) 个物品,第 \(i\) 个物品会占据 \(v_i\) 的空间,有着 \(w_i\) 的价值
你现在有着一个背包,这个背包的最大容积为 \(V\)
试求出你能携带的物品的价值总和的最大值
在这样一个问题中,我们可以这样定义状态:
使用 f[i][j] 表示状态
f[i][j]=(int)value
其中变量的含义是:
i - 当动态规划到第i个物品时(i<=n)
j - 令背包空间为j(j<=V)
(int)value - 此时的最大价值和
我们试着和上面的要求做一下比对
- 「状态」是一个数组 √
- 可以通过「状态」,在完成DP后计算出答案
- 在完成DP后,由于有 \(n\) 件物品,背包空间为 \(V\) ,所以答案是
f[n][V]√- 可以通过少量的公式/方程,完成不同「状态」的转移
- 这是下一节的内容,但是我可以告诉你这样定义是正确的( √
2、转移方程
动态规划最重要的一点就是转移方程的推导。转移方程是从一个状态推导到另一个状态时所依赖的公式,一个/一些正确的转移方程应该满足以下要求:
- 这个/这些转移方程应当覆盖了问题的所有情况
- 这个/这些转移方程用到的状态应当已被推导出
- 这个/这些转移方程的不同情况和决策应当一一对应
- 转移方程应当无后效性:即之后的决策不应影响到之前的决策
举个例子
用上面的 0/1背包 问题来举例子,我们想要试图推导出它的转移方程
因为对于每一个物品,我们都有放与不放两种选择,所以每一个物品的决策只有两种
如果我要把一个物品放进背包,那么要满足以下几点:
- 背包的空间足够放下这个物品
- 放下这个物品后,背包如果有剩余空间,剩余空间也要遵循最优解
因为我们把背包空间作为了状态的一个变量,所以第二点可以通过下面的方式满足:
//假设物品id为i
f[i][j]=f[i-1][j-v[i]]+w[i]
在上面的代码中,放入这个物品后,背包剩余空间为 j-v[i] ,这些剩余空间在前 i-1 件物品的决策中也应当有一个最优解,所以用 f[i-1][j-v[i]] 表示剩余空间的最优解。同时,由于放入了第 \(i\) 件物品,所以用 w[i] 表示第 \(i\) 个物品的价值
但是还没完,此时这个方程只覆盖了一种情况,我们要在这个方程的基础上写出完整的方程
公式版:
代码版:
for(int i=1;i<=n;i++){
for(int j=v[i];j<=V;j++){
f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
}
}
解释一下, \(j\) 的取值范围从 \(v_i\to i\) 而不是 \(1\to i\) ,是因为如果要把第 \(i\) 件物品放入背包,我们至少需要 \(v_i\) 的空间,所以不用考虑空间小于 \(v_i\) 的背包的情况
但是
这是一个二维数组,如果给定的 \(n\) 较大,这个数组的空间效率会比较底下
所以我们要对其空间进行优化
3. 优化
观察我们的转移方程,我们会发现:要求出 \(f_{(i,j)}\) ,我们只需要知道 \(f_{(i-1,*)}\) 。
换言之,要求出当前状态,我们只需要知道上一层状态即可
所以我们可以这样定义状态:
使用 f[i][j] 表示状态
f[i][j]=(int)value
其中变量的含义是:
i - 令背包空间为i(i<=V)
j - 0表示当前位,1表示前一位
(int)value - 此时的最大价值和
那么我们的转移方程相应变为:
for(int i=1;i<=n;i++){//枚举物品
for(int j=v[i];j<=V;j++){//枚举空间
f[j][0]=max(f[j][0],f[j-v[i]][1]+w[i]);
}
for(int j=1;j<=V;i++)f[j][1]=f[j][0];//拷贝结果
}
最后的答案就是 \(f_{(V,0)}\)
但是
我们还没有优化完成
我们再仔细地观察转移方程,我们会发现:要求出 \(f_{(j,0)}\) ,我们只需要知道 \(f_{(*\lt j,1)}\)
换言之,要求出当前状态,我们只需要知道上一层状态中空间小于当前状态的状态即可
可能有点绕,我们来模拟一下:
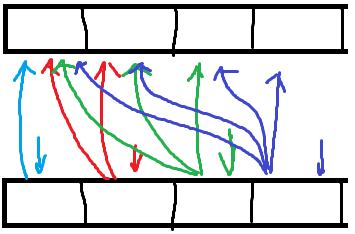
上面一排表示 \(f_{(*,1)}\) ,下面一排表示 \(f_{(*,0)}\) ,不同颜色的箭头表示对不同的空间大小进行决策时,根据放入的物品的大小,可能会访问的位置
所以我们可以只建一维数组
但是要注意一个问题:较小空间的决策会影响到较大空间的决策
举个例子,如果在 \(j=2\) 时决策放入了一个 \(v=2\) 的物品,然后在 \(j=4\) 时决策又将这个物品放了进去,这时背包的空间剩余为 \(2\) ,那么就会加上 \(j=2\) 时的结果。从结果而言,这个物品就被放入了两次,这与题目条件相悖。
解决方法也很简单:我们可以反向循环遍历空间大小。(不懂的可以自己模拟一下)
那么我们的转移方程就推导出来了
for(int i=1;i<=n;i++){//遍历物品
for(int j=V;j>=v[i];j--){//反向遍历空间
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
最后的答案就是 \(f_V\)
这条转移方程也是 0/1背包 问题的标准转移方程
0x01 0/1背包例题
[NOIP2005 普及组] 采药
题目描述
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
输入格式
第一行有 \(2\) 个整数 \(T\)(\(1 \le T \le 1000\))和 \(M\)(\(1 \le M \le 100\)),用一个空格隔开,\(T\) 代表总共能够用来采药的时间,\(M\) 代表山洞里的草药的数目。
接下来的 \(M\) 行每行包括两个在 \(1\) 到 \(100\) 之间(包括 \(1\) 和 \(100\))的整数,分别表示采摘某株草药的时间和这株草药的价值。
输出格式
输出在规定的时间内可以采到的草药的最大总价值。
I/O
样例输入 #1
70 3
71 100
69 1
1 2
样例输出 #1
3
提示
【数据范围】
- 对于 \(30\%\) 的数据,\(M \le 10\);
- 对于全部的数据,\(M \le 100\)。
【题目来源】
NOIP 2005 普及组第三题
这是一个标准的 0/1背包 问题,我们将题目中的条件转化为背包的内容:
\(T\) 是背包容量, \(M\) 是物品数量
对于每一株草药,采摘时间是物品所占的空间,草药的价值就是物品价值
所以可以很快的推导出方程:
#include <bits/stdc++.h>
using namespace std;
const int maxn=1012;
int T,M;
int v[maxn],w[maxn];//空间和价值
int f[maxn];//状态
void dp(){
for(int i=1;i<=M;i++){//枚举物品
for(int j=T;j>=v[i];j--){//倒叙枚举空间
f[j]=max(f[j],f[j-v[i]]+w[i]);//转移方程
}
}
}
int main(){
scanf("%d%d",&T,&M);
for(int i=1;i<=M;i++)
scanf("%d%d",&v[i],&w[i]);
dp();
printf("%d",f[T]);
return 0;
}
[NOIP2006 普及组] 开心的金明
题目描述
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过 \(n\) 元钱就行”。今天一早金明就开始做预算,但是他想买的东西太多了,肯定会超过妈妈限定的 \(n\) 元。于是,他把每件物品规定了一个重要度,分为 \(5\) 等:用整数 \(1-5\) 表示,第 \(5\) 等最重要。他还从因特网上查到了每件物品的价格(都是整数元)。他希望在不超过 \(N\) 元(可以等于 \(N\) 元)的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第 \(j\) 件物品的价格为 \(v[j]\) ,重要度为 \(w[j]\) ,共选中了 \(k\) 件物品,编号依次为 \(j_1,j_2,…,j_k\) ,则所求的总和为:
\(v[j_1] \times w[j_1]+v[j_2] \times w[j_2]+ …+v[j_k] \times w[j_k]\) 。
请你帮助金明设计一个满足要求的购物单。
输入格式
第一行,为 \(2\) 个正整数,用一个空格隔开: \(n,m\) (其中 \(n(<30000)\) 表示总钱数, \(m(<25)\) 为希望购买物品的个数。)
从第 \(2\) 行到第 \(m+1\) 行,第\(j\)行给出了编号为 \(j-1\) 的物品的基本数据,每行有\(2\)个非负整数 $ v\ p$ (其中 \(v\) 表示该物品的价格 \((v \le 10000)\) , \(p\) 表示该物品的重要度( \(1-5\) )
输出格式
\(1\) 个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的最大值 \((<100000000)\) 。
I/O
样例输入 #1
1000 5
800 2
400 5
300 5
400 3
200 2
样例输出 #1
3900
提示
NOIP 2006 普及组 第二题
这是一个不那么标准的 0/1背包 问题,我们将题目中的条件转化为背包的内容:
\(n\) 是背包容量, \(m\) 是物品数量
对于第 \(i\) 个物品, \(v_i\) 是物品所占的空间, \(v_i\times p_i\) 是物品的价值
所以可以很快的推导出方程:
#include<bits/stdc++.h>
using namespace std;
const int maxn=30012;
int n,m;
int v[maxn],w[maxn];//w[i]=v[i]*p[i],p[i]无需记录
int f[maxn];
void dp(){
for(int i=1;i<=m;i++){
for(int j=n;j>=v[i];j--){
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int tem;
scanf("%d%d",&v[i],&tem);
w[i]=v[i]*tem;
}
dp();
printf("%d",f[n]);
return 0;
}
0x02 完全背包
定义
完全背包问题是0/1背包问题的一个演化
在0/1背包中,每个物品只能被放入背包 \(1\) 次
在完全背包中,每个物品可以被放入背包无数次
解决思路
回忆一下我们是如何推导出0/1背包的转移方程的
但是要注意一个问题:较小空间的决策会影响到较大空间的决策
举个例子,如果在 \(j=2\) 时决策放入了一个 \(v=2\) 的物品,然后在 \(j=4\) 时决策又将这个物品放了进去,这时背包的空间剩余为 \(2\) ,那么就会加上 \(j=2\) 时的结果。从结果而言,这个物品就被放入了两次,这与题目条件相悖。
解决方法也很简单:我们可以反向循环遍历空间大小。(不懂的可以自己模拟一下)
这里就有很重要的一点:如果我们在遍历空间时正向遍历,那么一个物品就可以被放入背包多次
其实,这就是完全背包的解决方法:与0/1背包类似,但是在遍历空间时正向遍历
转移方程
for(int i=1;i<=n;i++){//遍历每一件物品
for(int j=v[i];j<=V;j++){//正向遍历空间
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
0x03 完全背包例题
[洛谷原创] 疯狂的采药
题目背景
此题为纪念 LiYuxiang 而生。
题目描述
LiYuxiang 是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同种类的草药,采每一种都需要一些时间,每一种也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是 LiYuxiang,你能完成这个任务吗?
此题和原题的不同点:
\(1\). 每种草药可以无限制地疯狂采摘。
\(2\). 药的种类眼花缭乱,采药时间好长好长啊!师傅等得菊花都谢了!
输入格式
输入第一行有两个整数,分别代表总共能够用来采药的时间 \(t\) 和代表山洞里的草药的数目 \(m\)。
第 \(2\) 到第 \((m + 1)\) 行,每行两个整数,第 \((i + 1)\) 行的整数 \(a_i, b_i\) 分别表示采摘第 \(i\) 种草药的时间和该草药的价值。
输出格式
输出一行,这一行只包含一个整数,表示在规定的时间内,可以采到的草药的最大总价值。
I/O
样例输入 #1
70 3
71 100
69 1
1 2
样例输出 #1
140
数据规模与约定
- 对于 \(30\%\) 的数据,保证 \(m \le 10^3\) 。
- 对于 \(100\%\) 的数据,保证 \(1 \leq m \le 10^4\),\(1 \leq t \leq 10^7\),且 \(1 \leq m \times t \leq 10^7\),\(1 \leq a_i, b_i \leq 10^4\)。
这是一个标准的完全背包问题,我们将题目中的条件转化为背包的内容:
\(t\) 是背包容量, \(m\) 是物品数量
对于每一株草药,采摘时间是物品所占的空间,草药的价值就是物品价值
所以可以很快的推导出方程:
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e7+12;
int T,M;
int v[maxn],w[maxn];//空间和价值
long long f[maxn];//状态
void dp(){
for(int i=1;i<=M;i++){//枚举物品
for(int j=T;j>=v[i];j--){//倒叙枚举空间
f[j]=max(f[j],f[j-v[i]]+w[i]);//转移方程
}
}
}
int main(){
scanf("%d%d",&T,&M);
for(int i=1;i<=M;i++)
scanf("%d%d",&v[i],&w[i]);
dp();
printf("%lld",f[T]);
return 0;
}
注意一点:最大可能的价值是:
maxb * maxt = 1e11
这超过了 INT_MAX=2147483647 ,因此要记得开 long long
0x04 多重背包
定义
多重背包问题是0/1背包问题的一个演化
在0/1背包中,每个物品只能被放入背包 \(1\) 次
在多重背包中,对于每个物品 \(i\) ,它能被放入背包 \(t_i\) 次
解决思路
暴力思路
我们可以把多重背包直接转化为0/1背包:
一共有 \(n\) 种物品,每种物品有 \(t_i\) 个
可以转化为:
一共有 \(\sum\limits_{i=1}^nt_i\) 个物品
这样就把多重背包转化为了0/1背包,复杂度是 maxt*maxn
正解
但是这样有些过于暴力,我们要想一个优化方案--二进制优化
有的人可能很疑惑:这要怎么二进制优化呢?
我们来思考一件事:想要表示出 \(0-20\) 中所有的正整数,我们会怎么办?
我们可以用二进制拆分:
原理:一个数字,我们可以按照二进制来分解成 1+2+4+8+...+2^k+余数
举个例子:
7可以分解为 1+2+4,也就是用 1,2,4 这三个数能表示 1-7 中的所有正整数
10 可以分解为 1+2+4+3 ,这个3就是余数
因此复杂度就降低到了 log(maxt)*maxn
转移方程
for(int i=1;i<=n;i++){//枚举物品种类
int bina = 1;//二进制拆分
while(num[i]-bina>0){//num[i]表示第i个物品的数目
num[i]-=bina;
for(int j=V;j>=v[i]*bina;j--)f[j]=max(f[j],f[j-bina*v[i]]+bina*w[i]);//0/1背包
bina<<=1;
}
for(int j=V;j>=v[i]*num[i];j--)f[j]=max(f[j],f[j-v[i]*num[i]]+num[i]*w[i]);//余数处理
}
0x05 多重背包例题
[NOI导刊] 宝物筛选
题目描述
终于,破解了千年的难题。小 FF 找到了王室的宝物室,里面堆满了无数价值连城的宝物。
这下小 FF 可发财了,嘎嘎。但是这里的宝物实在是太多了,小 FF 的采集车似乎装不下那么多宝物。看来小 FF 只能含泪舍弃其中的一部分宝物了。
小 FF 对洞穴里的宝物进行了整理,他发现每样宝物都有一件或者多件。他粗略估算了下每样宝物的价值,之后开始了宝物筛选工作:小 FF 有一个最大载重为 \(W\) 的采集车,洞穴里总共有 \(n\) 种宝物,每种宝物的价值为 \(v_i\),重量为 \(w_i\),每种宝物有 \(m_i\) 件。小 FF 希望在采集车不超载的前提下,选择一些宝物装进采集车,使得它们的价值和最大。
输入格式
第一行为一个整数 \(n\) 和 \(W\),分别表示宝物种数和采集车的最大载重。
接下来 \(n\) 行每行三个整数 \(v_i,w_i,m_i\)。
输出格式
输出仅一个整数,表示在采集车不超载的情况下收集的宝物的最大价值。
I/O
**样例输入 **
4 20
3 9 3
5 9 1
9 4 2
8 1 3
样例输出
47
提示
对于 \(30\%\) 的数据,\(n\leq \sum m_i\leq 10^4\),\(0\le W\leq 10^3\)。
对于 \(100\%\) 的数据,\(n\leq \sum m_i \leq 10^5\),\(0\le W\leq 4\times 10^4\),\(1\leq n\le 100\)。
这是一个标准的多重背包问题,我们将题目中的条件转化为背包的内容:
\(n\) 是物品种类数量, \(W\) 是背包空间
对于每一个宝物, \(v_i\) 是价值, \(w_i\) 是空间, \(m_i\) 是数量
所以可以很快的推导出方程:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 4e4+12;
int n,W;
int v[maxn],w[maxn],m[maxn];
int f[maxn];
void dp(){
for(int i=1;i<=n;i++){//枚举物品种类
int bina = 1;//二进制拆分
while(m[i]-bina>0){//num[i]表示第i个物品的数目
m[i]-=bina;
for(int j=W;j>=w[i]*bina;j--)f[j]=max(f[j],f[j-bina*w[i]]+bina*v[i]);//0/1背包
bina<<=1;
}
for(int j=W;j>=w[i]*m[i];j--)f[j]=max(f[j],f[j-w[i]*m[i]]+m[i]*v[i]);//余数处理
}
}
int main(){
scanf("%d%d",&n,&W);
for(int i=1;i<=n;i++)scanf("%d%d%d",&v[i],&w[i],&m[i]);
dp();
printf("%d",f[W]);
return 0;
}
0x06 分组背包
定义
分组背包问题是0/1背包问题的一个演化
在0/1背包中,每个物品都能被放入背包
在分组背包中,物品被划分为不同的组别,同组的物品相互冲突。
换言之,在分组背包中,放入背包的物品没有两个同组的
解决思路
我们可以把一组物品类比到0/1背包的一个物品:
- 与0/1背包相同的是,在分组背包中,每一组物品相当于只有一个(可以放入一个,或都不放)
- 与0/1背包不同的是,在分组背包中,对于每一组物品,我们一共有 \(物品数量+1\) 种决策方案(放入每组的第 \(i\) 个物品,或者都不放)
这要怎么解决呢?
我们思考一下在0/1背包中,我们是在什么时候进行决策的:(把代码中的 max 函数写开)
for(int i=1;i<=n;i++){//枚举物品
for(int j=V;j>=v[i];j--){//枚举空间
if(f[j]<f[j-v[i]]+w[i]){//进行决策
f[i]=f[j-v[i]]+w[i];
}
}
}
也就是说,在0/1背包中,我们是在枚举空间时进行决策
类比到分组背包,我们可以在枚举空间时依次决策每一个物品
于是推导出转移方程:
for(int i=1;i<=n;i++){//枚举组
for(int j=V;j>=1;j--){//枚举空间
for(int k=1;k<=num[i];k++){//枚举组内物品
if(j>=v[i][k]){//能够放下
f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);//决策
}
}
}
}
同样的,我们来推导一下这个转移方程的正确性
在对 f[j] 进行决策时,我们用到的只有 f[k],k<j 。而由于我们是倒序枚举空间的,所以同一组的物品至多被放入背包一个,方程正确
转移方程
for(int i=1;i<=n;i++){
for(int j=V;j>=1;j--){
for(int k=1;k<=num[i];k++){
if(j>=v[k]){
f[j]=max(f[j],f[j-v[k]]+w[k]);
}
}
}
}
0x07 分组背包例题
P1757 通天之分组背包
题目背景
直达通天路·小 A 历险记第二篇
题目描述
自 \(01\) 背包问世之后,小 A 对此深感兴趣。一天,小 A 去远游,却发现他的背包不同于 \(01\) 背包,他的物品大致可分为 \(k\) 组,每组中的物品相互冲突,现在,他想知道最大的利用价值是多少。
输入格式
两个数 \(m,n\),表示一共有 \(n\) 件物品,背包总重量为 \(m\)。
接下来 \(n\) 行,每行 \(3\) 个数 \(a_i,b_i,c_i\),表示物品的重量,利用价值,所属组数。
输出格式
一个数,最大的利用价值。
I/O
样例输入 #1
45 3
10 10 1
10 5 1
50 400 2
样例输出 #1
10
提示
\(1 \leq m, n \leq 1000\)。
这是一个标准的分组背包问题,我们将题目中的条件转化为背包的内容:
\(n\) 是物品种类数量, \(W\) 是背包空间
对于每一个宝物, \(v_i\) 是价值, \(w_i\) 是空间
但是我们需要注意把题目的输入转化为分组
所以可以很快的推导出方程:
#include<bits/stdc++.h>
using namespace std;
const int maxn=1012;
int m,n,g;//g -> 组别
int v[maxn][maxn],w[maxn][maxn],num[maxn];//空间/价值/每组数量
int f[maxn];
void dp(){
for(int i=1;i<=g;i++){
for(int j=m;j>=1;j--){
for(int k=1;k<=num[i];k++){
if(j>=v[i][k]){
f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
}
}
}
}
}
int main(){
scanf("%d%d",&m,&n);
for(int i=1;i<=n;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
g=max(g,c);
num[g]++;
v[g][num[g]]=a;
w[g][num[g]]=b;//数据转化
}
dp();
printf("%d",f[m]);
return 0;
}
0x08 多约束背包
定义
多约束背包问题是0/1背包问题的一种演化
在0/1背包中,背包只有空间限制,没有重量限制(或者其他的什么限制)
在多约束背包中,背包既有空间限制,也有重量限制
解决思路
和0/1背包类似,多约束背包也可以逆序枚举限制求解
注意:多约束背包的时间复杂度是 \(物品数量\times 限制1\times 限制2\times \cdots\times 限制k\) ,并且没有优化
转移方程
for(int i=1;i<=n;i++){//枚举物品
for(int j1=V1;j1>=v1[i];j1--){//枚举限制1
for(int j2=V2;j2>=v2[i];j2--){//枚举限制2
f[j1][j2]=max(f[j1][j2],f[j1-v1[i]][j2-v2[i]]+w[i]);
}
}
}
0x09 多约束背包例题
P1507 NASA的食物计划
题目背景
NASA(美国航空航天局)因为航天飞机的隔热瓦等其他安全技术问题一直大伤脑筋,因此在各方压力下终止了航天飞机的历史,但是此类事情会不会在以后发生,谁也无法保证,在遇到这类航天问题时,解决方法也许只能让航天员出仓维修,但是多次的维修会消耗航天员大量的能量,因此NASA便想设计一种食品方案,让体积和承重有限的条件下多装载一些高卡路里的食物.
题目描述
航天飞机的体积有限,当然如果载过重的物品,燃料会浪费很多钱,每件食品都有各自的体积、质量以及所含卡路里,在告诉你体积和质量的最大值的情况下,请输出能达到的食品方案所含卡路里的最大值,当然每个食品只能使用一次.
输入格式
第一行 两个数 体积最大值(<400)和质量最大值(<400)
第二行 一个数 食品总数N(<50).
第三行-第3+N行
每行三个数 体积(<400) 质量(<400) 所含卡路里(<500)
输出格式
一个数 所能达到的最大卡路里(int范围内)
I/O
样例输入 #1
320 350
4
160 40 120
80 110 240
220 70 310
40 400 220
样例输出 #1
550
这是一个标准的多约束背包问题,我们将题目中的条件转化为背包的内容:
对于每一个食品:所含卡路里就是其价值
所以可以很快的推导出方程:
#include<bits/stdc++.h>
using namespace std;
const int maxn=402;
int n,V,M;
int v[maxn],m[maxn],w[maxn];
int f[maxn][maxn];
void dp(){
for(int i=1;i<=n;i++){//枚举物品
for(int j1=V;j1>=v[i];j1--){//枚举空间
for(int j2=M;j2>=m[i];j2--){//枚举质量
f[j1][j2]=max(f[j1][j2],f[j1-v[i]][j2-m[i]]+w[i]);
}
}
}
}
int main(){
scanf("%d%d%d",&V,&M,&n);
for(int i=1;i<=n;i++){
scanf("%d%d%d",&v[i],&m[i],&w[i]);
}
dp();
printf("%d",f[V][M]);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号