小猴打架 题解

小猴打架 题解

P4430

题目大意

求一个 \(n\) 个节点的带序号树的生成方式的总数

解决方法

这种题看上去像图论，实际上是一道数论题

为了解决这道题，我们需要学习一下 \(prufer\) 编码

什么是 \(prufer\) 编码？

看不懂了吧？我也看不懂（

没关系，我们只需要知道， \(prufer\) 编码是一种珂以把一个带序号无根数转化为唯一数列的方法。

换句话说，每一棵有序号的无根数都有一个唯一对应的数列。

接下来我们来看一下如何把一棵树转化为 \(prufer\) 编码：

步骤

1. 找出所有叶子节点中编号最小的那个
2. 将这个节点删除，并将与之相邻的节点编号加入数列
3. 重复「1」「2」直到这棵树只剩两个节点

我们实际操作一下：

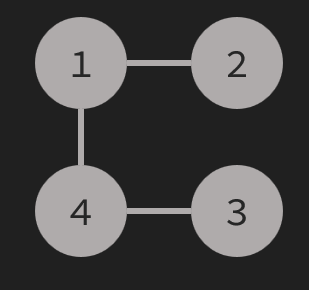
1. 删除「2」，将『1』加入数列。〔当前数列：『1』〕
2. 删除「1」，将『4』加入数列。〔当前数列：『1，4』〕

所以上面那个图的 \(prufer\) 编码就是 \([1,4]\)

---

好的，介绍完 \(prufer\) 编码，有什么用呢？

我们可以发现，实际上 \(prufer\) 编码的长度就是节点数减 \(2\) ，而它的每一位都是任意的（想想为什么？）

那么也就是说，对于 \(n\) 个节点，我们最多有 \(n^{(n-2)}\) 种不同的方式把他们连接为一棵树

而连接 \(n\) 条边的顺序有 \(n!\) 种

所以根据排列组合的原理，我们这道题的答案实际上就是\(n^{(n-2)}\times (n-1)!\)

AC代码

省略（