Luogu P2860 Redundant Paths 题解

P2860 题解

P2860 [USACO06JAN] Redundant Paths

题意：

至少需要多少条边才能使一张无向图变成一个强连通图？

I/O

I

7 7
1 2
2 3
3 4
2 5
4 5
5 6
5 7

O

2

基本思路

\(\color{white}{无向图\ 强连通}\) ，基本珂以肯定是 \(Tarjan\) 了。

那么问题就是如何处理 \(Tarjan\) 缩点后的结果。

我们先来模拟一下样例：

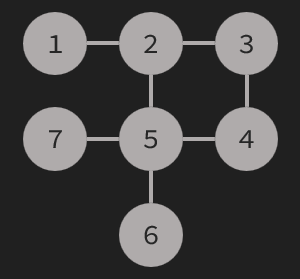
珂以发现，这张图被分为了 \(4\) 个 \(scc\) - \((2,3,4,5)\ (1)\ (6)\ (7)\)

而我们只需要添加 \(1\rightarrow 7\) 和 \(6 \rightarrow 7\) 两条无向边就珂以让这张图强连通，珂以证明，这张图中至少要添加两条边

我们再来观察这两条边的特征：

- 边所连接的scc都有且只有一条边与之相连
- 所有符合上面一条的点都被添加的边所连接

那么，由特殊到一般，我们进行一个推广：

> 命题：连接的是所有的没有子节点的scc后，这张图会形成一个强连通图

0. 证明：

1. 条件：这张图为连通图
2. 基本定理：Tarjan缩点后会形成一棵树
3. 基本定理：树的所有没有子节点的节点都是有且仅有一条边与之相连
4. 结论：本题中，要连接的scc都有且只有一条边与之相连
5. 结论：本题中，所有符合(4)的scc都被所添加的边所连接
6. 推论：由(3)(4)(5)珂知：本题中要连接的是所有的没有子节点的节点
7. 基本定理：无向图中，若一棵树的所有没有子节点的节点都被连接，那么这棵树会形成一个强连通图
8. 推论：由(6)(7)珂知：命题成立

所以，这道题需要求的边的数量就是连接所有没有子节点的scc所需的最小边数量

核心代码

\(Tarjan\) 就是标准的模板不多赘述，这里只讲解关于求边数量的代码

int ans=0;
for(int i = 1 ; i<=n ; i++)if(dfn[i]==0)Tarjan(i,0);
for(int i = 1 ; i<=len ; i++)if(belong[e[i].from]!=belong[e[i].to])d[belong[e[i].from]]++,d[belong[e[i].to]]++;
for(int i = 1 ; i<=scc ; i++)if(d[i]==2)ans++;
printf("%d\n",(ans+1)>>1);

我们一行一行地看

第一行：建立 \(ans\) 变量用于记录答案

第二行： \(Tarjan\) 模板

第三行：判断边的连接：其中 \(belong\) 记录一个点所属的 \(scc\) ， \(e\) 是存图的结构体， \(d\) 用于记录连接到对应 \(scc\) 的边的数量

第四行：统计叶子点的数量：因为是无向图，所以 \(d=2\) 意味着有一条边的连接

第五行：这个是重点了，我们展开说说：

当 \(ans\) 为偶数时，容易验证需要连接 \(\frac{ans}2\) 条边

当 \(ans\) 为奇数时，容易验证需要连接 \(\frac{ans+1}2\) 条边（相当于把多出来的那个连回去）

所以，用 \(C++\) 的思路来写，就珂以写出上面的表达式

AC代码