「笔记」DP简单笔记

概要

概念的穿插引入

降低算法复杂度的方法：利用问题的可划分性以及子问题之间的相似性进行归纳。

动态规划算法把原问题视作若干个重叠子问题的逐层递进，每个子问题的求解过程都构成一个“阶段”。

为了保证这些计算都能够按顺序且不重复执行，动态规划要求已经求解的子问题不受后续阶段的影响，这个条件被称为无后效性。动态规划对状态空间的遍历构成一张有向无环图，遍历顺序就是该有向无环图的一个拓扑序。有向无环图中的节点对应问题中的“状态”，图中的边则对应状态之间的“转移”，转移的选取就是动态规划中的“决策”。

同时在动态规划中，下一阶段的最优解应该能够由前面各阶段的子问题的最优解导出，这个条件被称为最优子结构性质。

三要素

状态、阶段、决策

使用 DP 的三个基本条件

子问题重叠性、无后效性、最优子结构性质

线性DP

线性DP，即线性动态规划，不局限于“线性时间复杂度”的一维动态规划。与数学中的“线性空间”相似，如果一个动态规划算法的状态包含多个维度，但在每个维度上都具有线性变化的阶段，那么该动态规划算法同样称为线性DP。

经典例题

LIS问题

即最长上升子序列问题。给定一个长度为 \(n\) 的数列 \(A\)，求数值单调递增的子序列的最长长度是多少。

问题名称	最长上升子序列
状态表示	\(f_i\) 表示以 \(A_i\) 为结尾的“最长上升子序列”的长度。
阶段划分	子序列的结尾位置（数列 \(A\) 的位置，从前到后）
转移方程	\(f_{i}=\max\limits_{0\le{j}\le{i},A_j<A_i}(f_j+1)\)
边界	\(f_0=0\)
目标	\(\max\limits_{i=1}^{n}f_i\)

LCS问题

即最长公共子序列问题。给定两个长度分别为 \(n\) 和 \(m\) 的数列 \(A\) 和 \(B\)。求两数列的最长公共子序列长度。

问题名称	最长公共子序列
状态表示	\(f_{i,j}\) 表示前缀子串 \(A_{1\sim i}\) 与 \(B_{1\sim j}\) 的最长公共子序列长度。
阶段划分	已经处理的前缀长度（两个数列中的位置，即一个二维坐标）
转移方程	\(f_{i,j}=\max\begin{cases}f_{i-1,j}\\{f_{i,j-1}}\\f_{i-1,j-1}+1(\text{if }A_{i}=B_{j})\end{cases}\)
边界	\(f_{i,0}=f_{0,j}=0\)
目标	\(f_{n,m}\)

数字三角形问题

给定一个共有 \(n\) 行的三角矩阵，从上到下的第 \(i\) 行有 \(i\) 列。现在从矩阵的左上角出发，每次可以向下方或者向右下方走一步，并获得该位置的数，加入到当前数的总和中，最终到达三角矩阵的底层。求到达底层能获得的最大和。

问题名称	数字三角形
状态表示	\(f_{i,j}\) 从左上角走到第 \(i\) 行第 \(j\) 列所得到的最大的和是多少。
阶段划分	路径的结尾位置（即矩阵中的行和列，一个二维坐标）
转移方程	\(f_{i,j}=\max\begin{cases}f_{i-1,j}\\{f_{i-1,j-1}}\end{cases}+a_{i,j}\)
边界	\(f_{1,1}=a_{1,1}\)
目标	\(\max\limits_{i=1}^n({f_{n,i}})\)

容易发现，不管表示的状态是一维还是多维，DP算法在这些问题上都体现为作用在线性空间上的递推——DP的阶段沿着各个维度线性增长，从一个或多个边界点开始有方向地向整个状态空间转移、扩展，最终每个状态上都保留了以自身为目标的最优解。

【例题】AcWing271 杨老师的照相排列

题目分析：

因为在合法方案中，每行每列的身高都是单调的，所以我们可以从高到低依次考虑标记为 \(1,2,\dots, n\) 的学生站的位置，发现 \(k\) 很小，所以可以考虑直接对每一排开一维数组，也就是开一个五维数组。当安排一名新的学生时，只需满足 \(a_i<N_i\) 且 \(i=1\) 或 \(a_{i-1}>a_i\) 即可。

状态：

用 \(f_{a_1,a_2,a_3,a_4,a_5}\) 表示各排从左端起点分别站了 \(a_1,a_2,a_3,a_4,a_5\) 个人时，合影方案数量，\(k<5\) 的排用 \(0\) 替代即可。

边界：

\(f_{0,0,0,0,0}=1\)。

转移：

若 \(a_1< N_1\)，那么令 \(f_{a_1+1,a_2,a_3,a_4,a_5}+=f_{a_1,a_2,a_3,a_4,a_5}\)。

若 \(a_2<N_2\)，那么令 \(f_{a_1,a_2+1,a_3,a_4,a_5}+=f_{a_1,a_2,a_3,a_4,a_5}\)。

第 \(3\sim5\) 排同理。

答案：

\(f_{N_1,N_2,N_3,N_4,N_5}\)。

代码：

#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
#define ll long long
using namespace std;

const int A = 31;
const int B = 1e6 + 11;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;

inline int read() {
  char c = getchar();
  int x = 0, f = 1;
  for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
  for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
  return x * f;
}

int k, cn[6];
ll f[A][A][A][A][A];

int main() {
  while (k = read()) {
    if (k == 0) return 0;
    memset(cn, 0, sizeof(cn));
    for (int i = 1; i <= k; i++) cn[i] = read();
    memset(f, 0, sizeof(f));
    f[0][0][0][0][0] = 1;
    for (int a = 0; a <= cn[1]; a++)
      for (int b = 0; b <= min(a,cn[2]); b++)
        for (int c = 0; c <= min(b, cn[3]); c++)
          for (int d = 0; d <= min(c, cn[4]); d++)
            for (int e = 0; e <= min(d, cn[5]); e++) {
              ll &x = f[a][b][c][d][e];
              if (a && a - 1 >= b) x += f[a - 1][b][c][d][e];
              if (b && b - 1 >= c) x += f[a][b - 1][c][d][e];
              if (c && c - 1 >= d) x += f[a][b][c - 1][d][e];
              if (d && d - 1 >= e) x += f[a][b][c][d - 1][e];
              if (e) x += f[a][b][c][d][e - 1];
            }
    cout << f[cn[1]][cn[2]][cn[3]][cn[4]][cn[5]] << '\n';
  }
  return 0;
}

【例题】AcWing272 LCIS 最长公共上升子序列

题目分析

此题为 LCS 和 LIS 的综合。但是不同的是公共的概念并不同，这点需要注意。将两算法结合，容易想到以下解法：

问题名称	最长公共上升子序列
状态表示	\(f_{i,j}\) 表示 \(A_{1\sim{i}}\)、\(B_{1\sim{j}}\) 可以构成的以 \(B_j\) 为结尾的最长公共上升子序列的长度。
阶段划分	已经处理的前缀长度（两个数列中的位置，即一个二维坐标）。
转移方程	\(f_{i,j}=\begin{cases}f_{i-1,j}&A_i\ne{B_j}\\\max\limits_{0\le{k}<j,B_{k}<{A_i}}(f_{i-1,k})+1&{A_i=B_j}\end{cases}\)
边界	\(f_{0,0}=0\)
目标	\(\max\limits_{j=1}^m\{f_{n,j}\}\)

显然以上状态转移可以用三重循环的方式计算。但是这样肯定是过不了这道题的，时间复杂度的 \(O(n^3)\) 无法过掉 \(n,m\le3000\)。

因此考虑优化：在转移过程中，我们把满足 \(0\le{k}<{j},{B_k}<{A_i}\) 的 \(k\) 构成的集合称为 \(f_{i,j}\) 进行状态转移时的决策集合，记为 \(S(i,j)\)。注意到第二层循环时当 \(j\) 从 \(1\) 增加到 \(m\) 时，第一层循环 \(i\) 是一个定值，这使得 \(B_k<A_i\) 是固定的。因此当变量 \(j\) 加 \(1\) 时，\(k\) 的取值范围由 \(0\le{k}<{j}\) 变为 \(0\le{k}<{j+1}\)，即整数 \(j\) 可能会进入新的决策集合，所以我们只需要 \(O(1)\) 检查 \(B_j\le{A_i}\) 是否满足，若满足则尝试更新当前取值。

\[S(i,j+1)=\begin{cases}S(i,j)&A_{i}\le{B_j}\\S(i,j)\bigcup{j}&A_i>{B_j}\end{cases} \]

所以上述式子只要 \(O(n^2)\) 时间内就可以解决，最终的目标即为 \(\max\limits_{j=1}^m\{f_n,j\}\)。

ps：AcWing 上的这道题 \(n=m\)。

#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int A = 3e3 + 11;
const int B = 1e6 + 11;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;

inline int read() {
  char c = getchar();
  int x = 0, f = 1;
  for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
  for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
  return x * f;
}

int n, a[A], b[A], f[A][A];

int main() {
  n = read();
  for (int i = 1; i <= n; i++) a[i] = read();
  for (int i = 1; i <= n; i++) b[i] = read();
  for (int i = 1; i <= n; i++) {
    int val = 0;
    if (b[1] < a[i]) val = f[i - 1][0];
    for (int j = 2; j <= n; j++) {
      if (b[j] == a[i]) f[i][j] = max(f[i][j], val + 1);
      else f[i][j] = f[i - 1][j];
      if (b[j] < a[i]) val = max(val, f[i - 1][j]);
    }
  }
  int ans = 0;
  for (int j = 1; j <= n; j++) ans = max(ans, f[n][j]);
  cout << ans << '\n';
}

此题转移部分的优化告诉我们，在实现状态转移方程时，要注意观察决策集合的范围随着状态的变化情况。对于“决策集合中的元素只增多不减少”的情景，就可以像此题一样维护一个变量来记录决策集合的当前信息，避免重复扫描，把转移的复杂度降低一个量级。

【例题】AcWing273 分级

题目分析

一个性质：一定存在一组最优解 \(B\)，使得每一个 \(B_i\) 都在 \(A\) 数组中出现过。

证明：

此处以单调不降为例。

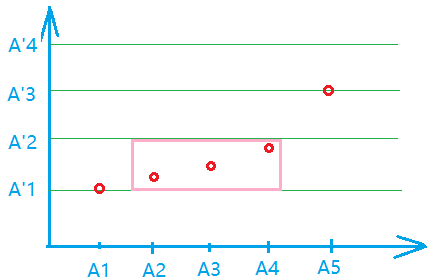
假设某个解如下图所示，其中 \(A\) 是原序列， \(A'\) 是将原序列排序后的序列，红圆圈表示每个 \(B_i\)。

考虑位于 \(A'_i,A'_{i+1}\) 之间的一段 \(B_i\)，如上图中粉色框框出的部分。

则在 \(A\) 中粉色框对应的这一段中统计出大于等于 \(A'_{i+1}\) 的数的数量 \(x\)，小于 \(A_i\) 的数的数量 \(y\)，那么：

如果 \(x>y\) 则可以令粉色框中的 \(B_i\) 整体上移直到其中一个 \(B_i\) 碰到上边界使答案更优。

如果 \(x<y\) 则可以令粉色框中的 \(B_i\) 整体下移直到其中一个 \(B_i\) 碰到下边界使答案更优。

如果 \(x=y\) 则上述两种方式均可。

所以只要存在某个 \(B_i\) 的值不在原序列中，就可以将其挪到与原数列中某个数相同的位置，且答案不会变差。

用 \(f_{i,j}\) 表示已经排好了 \(B_{1\sim{i}}\) 且 \(B_i=A'_j\) 的最小花费。

依据倒数第二个数分配的是哪一个 \(A'_i\) 将 \(f_{i,j}\) 所代表的集合划分成 \(j\) 个不重不漏的子集。

#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int A = 2e3 + 11;
const int B = 1e6 + 11;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;

inline int read() {
  char c = getchar();
  int x = 0, f = 1;
  for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
  for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
  return x * f;
}

int n, m, a[A], b[A], f[A][A], ans = inf; 

inline void DP() {
  memset(f, 0, sizeof(f));
  for (int i = 1; i <= n; i++) {
    int minn = inf;
    for (int j = 1; j <= m; j++) {
      minn = min(minn, f[i - 1][j]);
      f[i][j] = minn + abs(a[i] - b[j]);
    }
  }
  for (int i = 1; i <= m; i++) ans = min(ans, f[n][i]);
}

int main() {
  n = read();
  for (int i = 1; i <= n; i++) b[i] = a[i] = read();
  sort(b + 1, b + 1 + n);
  m = unique(b + 1, b + 1 + n) - b - 1;
  DP();
  reverse(a + 1, a + 1 + n);
  DP();
  cout << ans << '\n';
  return 0;
}

【例题】AcWing274 移动服务

容易发现DP的“阶段”就是“已经完成的请求数量”，通过指派一名服务员，可以从完成 \(i-1\) 个请求转移到完成 \(i\) 个请求。

不妨记录三个服务员的位置，将三个服务员的位置也放到DP的“状态”中，设 \(f_{i,x,y,z}\) 表示：完成了 \(i\) 个请求，三个服务员分别位于 \(x,y,z\) 时的最小花费。

那么容易想到转移方程有：

f[i][p[i+1]][y][z]=min(f[i][p[i+1]][y][z],f[i][x][y][z]+c[x][p[i+1]])
f[i][x][p[i+1]][z]=min(f[i][x][p[i+1]][z],f[i][x][y][z]+c[y][p[i+1]])
f[i][x][y][p[i+1]]=min(f[i][x][y][p[i+1]],f[i][x][y][z]+c[z][p[i+1]])

注意要特判每个位置不能相同，意义也比较明确，所以就不多说了。

但是这个算法的规模巨大，在 \(1000\times200^3\) 这个量级，肯定是不能承受的。但是我们发现当前一定有一个位置位于 \(p_i\)，所以只需要知道阶段 \(i\) 和另外两名员工的位置即可描述一个状态，因此可以直接用 \(f_{i,x,y}\) 表示完成了前 \(i\) 个请求，其中一个员工位于 \(p_i\)，其他两个员工分别位于 \(x\) 和 \(y\) 时的最小花费。之后的三种转移分别是让位于 \(p_{i},x,y\) 之一的员工前往 \(p_{i+1}\) 处理请求。

\[{\begin{cases}f_{i+1,x,y}=\min(f_{i+1,x,y},f_{i,x,y}+c_{p_{i},p_{i+1}})\\f_{i+1,p_{i},y}=\min(f_{i+1,p_{i},y},f_{i,x,y}+c_{x,p_{i+1}})\\f_{i+1,x,p_{i}}=\min(f_{i+1,x,p_{i}},f_{i,x,y}+c_{y,p_{i+1}})\end{cases}} \]

设 \(p_{0}=3\)，则可以初始化 \(f_{0,1,2}=0\)，最后的答案就是 \(\min\limits_{1\le{i},{j}\le{L}}f_{n,i,j}\)

#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int A = 1010;
const int B = 211;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;

inline int read() {
  char c = getchar();
  int x = 0, f = 1;
  for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
  for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
  return x * f;
}

int l, n, p[A], c[B][B], f[A][B][B];

int main() {
  l = read(), n = read();
  for (int i = 1; i <= l; i++)
    for (int j = 1; j <= l; j++) c[i][j] = read();
  for (int i = 1; i <= n; i++) p[i] = read();
  memset(f, inf, sizeof(f));
  f[0][1][2] = 0, p[0] = 3;
  for (int i = 0; i < n; i++) {
    for (int x = 1; x <= l; x++) {
      for (int y = 1; y <= l; y++) {
        if (x == y || x == p[i] || y == p[i]) continue;
        f[i + 1][x][y] = min(f[i][x][y] + c[p[i]][p[i + 1]], f[i + 1][x][y]);
        f[i + 1][p[i]][y] = min(f[i][x][y] + c[x][p[i + 1]], f[i + 1][p[i]][y]);
        f[i + 1][x][p[i]] = min(f[i][x][y] + c[y][p[i + 1]], f[i + 1][x][p[i]]);
      }
    }
  }
  int ans = inf;
  for (int i = 1; i <= l; i++)
    for (int j = 1; j <= l; j++) ans = min(ans, f[n][i][j]);
  cout << ans << '\n';
  return 0;
}

启发

求解线性DP问题，一般先确定阶段。若阶段不足以表示一个状态，可以把所需的附加信息也作为状态的维度。
若转移时总是从一个阶段转移到下一个阶段，则没有必要关心附加信息维度的大小变化情况，因为无后效性已经由“阶段”保证。
在确定DP状态时，要选择最小的能够覆盖整个状态空间的“维度集合”。若DP状态由多个维度构成，则可以思考一下能否由几个维度推出另一个维度，从而降低空间复杂度。

【例题】AcWing275 传纸条

把路径长度作为DP的“阶段”，同时还要确定两条路径当前的末尾位置。设路径长度为 \(i\)，第一条路径末尾位置位于 \(({x_1},{y_1})\)，第二条路径末尾位置位于 \(({x_2},{y_2})\)。根据上一道例题的启发，我们要思考一下能否由几个维度推出另一些维度。

\(f_{k, i, j}\) 表示两个人同时走了 \(k\) 步，第一个人在 \((i, k - i)\) 处，第二个人在 \((j, k - j)\) 处的所有走法的最大分值。

转移：按照最后一步两个人的走法分成四种情况进行转移。

#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int A = 55;
const int B = 1e6 + 11;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;

inline int read() {
  char c = getchar();
  int x = 0, f = 1;
  for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
  for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
  return x * f;
}

int n, m, val[A][A], f[A << 1][A][A];

int main() {
  n = read(), m = read();
  for (int i = 1; i <= n; i++)
    for (int j = 1; j <= m; j++) val[i][j] = read();
  for (int k = 2; k <= n + m; k++)
    for (int i = max(1, k - m); i <= n && i < k; i++)
      for (int j = max(1, k - m); j <= n && j < k; j++)
        for (int a = 0; a <= 1; a++)
          for (int b = 0; b <= 1; b++) {
            int now = val[i][k - i];
            if (i != j || k == 2 || k == n + m) {
              now += val[j][k - j];
              f[k][i][j] = max(f[k][i][j], f[k - 1][i - a][j - b] + now);
            }
          }
  cout << f[n + m][n][n] << '\n';
  return 0;
}

不想写的例题

AcWing276

在动态规划问题需要给出方案时，通常做法是额外使用一些与DP状态大小相同的数组记录下来每个状态的“最优解”是从何处转移而来的。最终用 DP 求出最优解后，通过一次递归，沿着记录的每一步“转移来源”回到初态，即可得到一条从初态到最优解的转移路径，也就是所求的具体方案。

AcWing277 饼干

题目分析

比较巧妙的转化，但是输出方案的时候出了问题，迫使我看了y总的输出方案代码……不知道自己的为啥不行，放坑了

首先一个性质：贪婪度越大的孩子获得的饼干数应该越多。证明也不难证，直接用贪心中的临项交换法就行了，不再赘述。因此我们可以把小朋友按照贪婪值从大到小排序，这样之后他们分配到的饼干数量是单调递减的。

状态设计：设 \(f_{i,j}\) 表示前 \(i\) 个小朋友分了 \(j\) 块饼干所得到的最小怨气值总和。

状态转移：

如果第 \(i\) 个小朋友获得的饼干数不为 \(1\) 且 \(j>=i\)，那么 \(f_{i,j}\) 的一个可行选择为 \(f_{i,j-i}\)，这两个式子是等价的，前 \(i\) 个小朋友分了 \(j\) 块饼干等价于前 \(i\) 个小朋友分了 \(j-i\) 块饼干，原因是这样相当于每个人少拿一块饼干，但是获得的饼干数量的相对顺序是不变的，所以怨气值之和也是不会变的。
如果第 \(i\) 个小朋友获得的饼干数为 \(1\)，那么就可以枚举前面有多少个小朋友获得的饼干数为 \(1\)，从中取最小值，这一步可以用前缀和优化。

由此可得整个DP的转移方程为：

\[f_{i,j}=\min\begin{cases}f_{i,j-i}&\text{if } j\ge i\\\min\limits_{k=0}^{i-1}(f_{k,j-(i-k)}+k\times\sum\limits_{x=k+1}^{i}g_x)&\text{if }j\ge(i-k)\end{cases} \]

初始条件为 \(f_{0,0}=0\)，最终目标为 \(f_{n,m}\)。

输出方案有点迷……

代码

#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
#define pii pair <int, int>
using namespace std;

const int A = 33;
const int B = 5011;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;

inline int read() {
  char c = getchar();
  int x = 0, f = 1;
  for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
  for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
  return x * f;
}

pii g[A];
int n, m, f[A][B], sum[A], ans[A];

int main() {
  n = read(), m = read();
  for (int i = 1; i <= n; i++) {
    g[i].first = read();
    g[i].second = i;
  }
  sort(g + 1, g + 1 + n);
  reverse(g + 1, g + 1 + n);
  for (int i = 1; i <= n; i++) 
    sum[i] = sum[i - 1] + g[i].first;
  memset(f, inf, sizeof(f));
  f[0][0] = 0;
  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
      if (j >= i) f[i][j] = f[i][j - i];
      for (int k = 0; k < i && j >= (i - k); k++)
        f[i][j] = min(f[i][j], f[k][j - (i - k)] + k * (sum[i] - sum[k]));
    }
  }
  cout << f[n][m] << '\n';
  int i = n, j = m, h = 0;
  while (i && j) {
    if (j >= i && f[i][j] == f[i][j - i]) j -= i, h++;
    else {
      for (int k = 1; k <= i && k <= j; k++) {
        if (f[i][j] == f[i - k][j - k] + (i - k) * (sum[i] - sum[i - k])) {
          for (int x = i; x > i - k; x--) ans[g[x].second] = 1 + h;
          i -= k, j -= k;
          break;
        }
      }
    }
  }
  for (int i = 1; i <= n; i++) cout << ans[i] << " ";
  puts("");
  return 0;
}

背包DP

比较简单了，随便写写

0/1背包

有 \(n\) 件物品和一个容量为 \(M\) 的背包。第 \(i\) 件物品的体积是 \(V_i\)，价值是 \(W_i\)。求解将哪些物品装入背包且容量不超过 \(M\) 可使价值总和最大。

\(f_{i,j}\)表示前 \(i\) 件物品恰放入一个容量为 \(j\) 的背包可以获得的最大价值，转移方程为

\[f_{i,j}=\max\begin{cases}f_{i-1,j}\\f_{i-1,j-V_i}+W_i&\text{if }{j}\ge{V_i}\end{cases} \]

初始化 \(f_{0,0}=0\)，目标为 \(\max\limits_{i=0}^{m}{f_{n,i}}\)。

for (int i = 1; i <= n; i++) {
  for (int j = 0; j <= m; j++) {
    if (j < v[i]) f[i][j] = f[i - 1][j];
    else f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
  }
}

可以用滚动数组优化空间。

int f[2][maxn_M+1];
int now = 0, last = 1;
for (int i = 1; i <= n; i++) {
  swap(now, last);
  for (int j = 0; j <= m; j++) {
    if (j < v[i]) f[now][j] = f[last][j];
    else f[now][j] = max(f[last][j], f[last][j - v[i]] + w[i]);
  }
}

其实可以直接压掉第一维，此时第二维需要使用倒序枚举的方法。

我是代码
我是01背包压维的代码

AcWing278 数字组合

01背包板子题。

#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int A = 1e5 + 11;
const int B = 1e6 + 11;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;

inline int read() {
  char c = getchar();
  int x = 0, f = 1;
  for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
  for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
  return x * f;
}

int n, m, f[A], a[A];

int main() {
  n = read(), m = read();
  f[0] = 1;
  for (int i = 1; i <= n; i++) a[i] = read();
  for (int i = 1; i <= n; i++) 
    for (int j = m; j >= a[i]; j--) f[j] += f[j - a[i]]; 
  cout << f[m] << "\n";
  return 0;
}

完全背包

有 \(n\) 种物品和一个容量为 \(M\) 的背包。每种物品都有无限个，第 \(i\) 种物品的体积是 \(V_i\)，价值是 \(W_i\)。求解将哪些物品装入背包且容量不超过 \(M\) 可使价值总和最大。

\(f_{i,j}\)表示前 \(i\) 件物品恰放入一个容量为 \(j\) 的背包可以获得的最大价值，转移方程为

\[f_{i,j}=\max\begin{cases}f_{i-1,j}\\f_{i,j-V_i}+W_i&\text{if }{j}\ge{V_i}\end{cases} \]

初始化 \(f_{0,0}=0\)，目标为 \(\max\limits_{i=0}^{m}{f_{n,i}}\)。

同样可以压掉一维，但是正序枚举就可以了，因为一个物品可以选多次。

int f[100010], n, m, v[A], w[A];
for (int i = 1; i <= n; i++) 
  for (int j = v[i]; j <= m; j++) 
    f[j] = max(f[j], f[j - v[i]] + w[i]);
int ans = 0;
for (int i = 0; i <= m; i++) ans = max(ans, f[i]);
cout << ans << '\n';

AcWing279 自然数拆分

还是板子题……

#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
#define int long long
using namespace std;

const int A = 1e5 + 11;
const int B = 1e6 + 11;
const int mod = 2147483648;

inline int read() {
  char c = getchar();
  int x = 0, f = 1;
  for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
  for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
  return x * f;
}

int n, f[A];

signed main() {
  n = read();
  f[0] = 1;
  for (int i = 1; i < n; i++) {
    for (int j = i; j <= n; j++) {
      f[j] = (f[j] + f[j - i]) % mod;
    }
  }
  cout << f[n] << '\n';
  return 0;
}

AcWing280 陪审团

#include <bits/stdc++.h>
#define mem(x) memset(x, 0, sizeof(x))
using namespace std;
const int MAXN = 205;
int drr[MAXN], prr[MAXN], dp[25][805], lujing[25][805][500];
void Init() {
	mem(drr), mem(prr), mem(lujing);
	for(int i = 0; i < 25; i ++) {
		for(int j = 0; j < 805; j ++) {
			dp[i][j] = -1;
		}
	}
	dp[0][400] = 0;
}
int n, m;
int main() {
	int step = 0;
	while(~scanf("%d%d", &n, &m) && (n || m)) {
		Init();
		for(int i = 1; i <= n; i ++) {
			scanf("%d%d", &drr[i], &prr[i]);
		}
		for(int i = 1; i <= n; i ++) {
			for(int j = m; j > 0; j --) {
				for(int k = 0; k <= 800; k ++) {
					if(k - (drr[i] - prr[i]) >= 0 && dp[j - 1][k - (drr[i] - prr[i])] >= 0 && k - (drr[i] - prr[i]) <= 800) {
						if(dp[j - 1][k - (drr[i] - prr[i])] + drr[i] + prr[i] > dp[j][k]) {
							dp[j][k] = dp[j - 1][k - (drr[i] - prr[i])] + drr[i] + prr[i];
							lujing[j][k][dp[j][k]] = i;
						}
					}
				}
			}
		}
		int sum = 0x7fffffff;
		int num = 0;
		int re = 0;
		int flag = 0;
		for(int k = 0; k <= 800; k ++) {
			if(k <= 400) {
				int temp = 400 - k;
				if(temp < sum && dp[m][k] >= 0) {
					sum = temp;
					num = dp[m][k];
					re = k;
					flag = 0;
				} else if(temp == sum && dp[m][k] >= num) {
					num = dp[m][k];
					re = k;
					flag = 0;
				}
			} else {
				int temp = k - 400;
				if(temp < sum && dp[m][k] >= 0) {
					sum = temp;
					num = dp[m][k];
					re = k;
					flag = 1;
				} else if(temp == sum && dp[m][k] >= num) {
					num = dp[m][k];
					re = k;
					flag = 1;
				}
			}
		}
		int a, b;
		if(flag == 1) {
			a = (sum + num) / 2;
			b = num - a;
		} else {
			a = (num - sum) / 2;
			b = num - a;
		}
		printf("Jury #%d\n", ++ step);
		printf("Best jury has value %d for prosecution and value %d for defence:\n", a, b);
		vector<int>vec;
		vec.clear();
		int k = re;
		int mysum = dp[m][k];
		while(lujing[m][k][mysum]) {
			vec.push_back(lujing[m][k][mysum]);
			int temp = lujing[m][k][mysum];
			m --;
			k = k - (drr[temp] - prr[temp]);
			mysum = mysum - drr[temp] - prr[temp];
		}
		sort(vec.begin(), vec.end());
		for(int i = 0; i < vec.size(); i ++) {
			printf(" %d", vec[i]);
		}
		printf("\n\n");
	}
	return 0;
}

多重背包

给定 \(n\) 种物品，其中第 \(i\) 种物品的体积为 \(V_i\)，价值为 \(W_i\)，并且有 \(C_i\) 个，求最大价值

咕了……很简单

直观的方法是把每种物品直接分成 \(c_i\) 个，但是效率很低
因此可以用二进制拆分或者单调队列来优化

AcWing281 硬币

多重背包。这道题目中没有“物品价值”属性，不是一个最优化问题，而是一个可行性问题，所以可以考虑贪心：设 \(used_{j}\) 表示 \(f_j\) 在阶段 \(i\) 为 true 时至少需要多少枚第 \(i\) 种硬币。也就是说，在 \(f_{j-a_i}\) 为 true 时，如果 \(f_{j}\) 已经为 true，则不执行 DP 的转移，并令 \(used_{j}=0\)，否则才执行 \(f_{j}=f_{j}\lor f_{j-a_{i}}\) 的转移，并令 \(used_{j}=used_{j-a_{i}}+1\)。

核心代码如下：

int used[100010];
for (int i = 1; i <= n; i++) {
  for (int j = 0; j <= m; j++) used[j] = 0;
  for (int j = a[i]; j <= m; j++) 
    if (!f[j] && f[j - a[i]] && used[j - a[i]] < c[i])
	  f[j] = true, used[j] = used[j - a[i]] + 1;
}

分组背包

给定 \(n\) 组物品，其中第 \(i\) 组中有 \(C_i\) 个物品。第 \(i\) 组的第 \(j\) 个物品的体积为 \(V_{i,j}\)，价值为 \(W_{i,j}\)。有一个容积为 \(M\) 的背包，要求选出若干个物品，使得每组至多选择一个物品且物品总体积不超过 \(M\) 的前提下选出物品的价值和最大。

用 \(f_{i,j}\) 表示从前 \(i\) 组中选出总体积为 \(j\) 的物品放入背包，物品的最大价值和。

\[f_{i,j}=\max\begin{cases}f_{i-1,j}\\\max\limits_{1\le{k}\le{C_i}}(f_{i - 1, j - v_{i,k}}+w_{i,k})\end{cases} \]

与前面几个模型一样，同样可以压维。

f[0] = 0;
for (int i = 1; i <= n; i++)
  for (int j = m; j >= 0; j--)
    for (int k = 1; k <= c[i]; k++)
      if (j > v[i][k]) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);

区间DP

posted @ 2020-11-10 22:17 Loceaner 阅读(131) 评论(0) 编辑收藏举报

刷新页面返回顶部

Forever Young

Loceaner's Blog

「笔记」DP简单笔记

概要

概念的穿插引入

三要素

使用 DP 的三个基本条件

线性DP

经典例题

LIS问题

LCS问题

数字三角形问题

【例题】AcWing271 杨老师的照相排列

题目分析：

状态：

边界：

转移：

答案：

代码：

【例题】AcWing272 LCIS 最长公共上升子序列

题目分析

【例题】AcWing273 分级

题目分析

【例题】AcWing274 移动服务

启发

【例题】AcWing275 传纸条

不想写的例题

AcWing276

AcWing277 饼干

题目分析

代码

背包DP

0/1背包

AcWing278 数字组合

完全背包

AcWing279 自然数拆分

AcWing280 陪审团

多重背包

AcWing281 硬币

分组背包

区间DP

公告