网络流总结
二分图
定义
二分图定义:
如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集,则称图G为一个二分图。
就是说,能把节点划分为两个部分,使得同一部分里没有边的图。
或者,没有长度为奇数的环的图也是二分图。
判定
使用黑白染色,若一个点为黑色,则他周围的点都是白色,反之是黑色。
匹配
匈牙利算法:这里
这个算法我不太用,我主要用最大流进行匹配。
最大独立集
最大独立集=点数-最大匹配数。
证明,构造:后面
最小顶点覆盖
最小顶点覆盖=最大匹配数。
原因:显然,把图中的最大独立集去掉,就变成了最小顶点覆盖。
所以,最小顶点覆盖=点数-最大独立集=最大匹配数。
证明,构造:后面
最小边覆盖
最小边覆盖=点数-最大匹配数。
证明,构造方法:
贪心,先选最大匹配中的边,剩下的点每个任意选一条边进行覆盖。
所以,最小边覆盖=最大匹配数+(点数-最大匹配数×2)=点数-最大匹配数。
最佳完美匹配
KM算法讲解
理解:
贪心算法,每个结点都要匹配。
对每个左边的结点进行匹配,尽量使用最大的匹配。
但是,普通的匈牙利算法在找增广路时,无法保证匹配的权值。
所以,我们将每个结点附加一个数值,每次寻找匹配时都满足匹配边权等于两点附加值之和。
这样,就可以控制损失的权值了。
具体实现如下:
使用类似匈牙利的算法,在增广时限制匹配边。
每次增广,保证右面的结点每个最多被匹配一次。
若增广失败,设x为改变情况要下降的最小值。
将参与匹配的左面的结点都减x,右面的结点都加x。
这样,原先匹配过的边还能匹配,并且没匹配过的左边就回不到匹配过的右边了。
这样,在匹配时,就会走到之前未匹配的结点。
然后,就是将总权值降低了x。
代码:
#include <stdio.h>
int sz[110][110],inf=99999999;
bool vg[110],vb[110];
int exg[110],exb[110];
int sl[110],pp[110],n;
bool dfs(int u)
{
vg[u]=true;
for(int i=0;i<n;i++)
{
if(vb[i])//只访问一次
continue;
int t=exg[u]+exb[i]-sz[u][i];
if(t==0)//此边可用
{
vb[i]=true;
if(pp[i]==-1||dfs(pp[i]))
{
pp[i]=u;
return true;//找到增广路
}
}
else
{
if(t<sl[i])//更新最小下降值
sl[i]=t;
}
}
return false;
}
void KM()
{
for(int i=0;i<n;i++)
pp[i]=-1;
for(int i=0;i<n;i++)
{
exb[i]=0;
exg[i]=-inf;
for(int j=0;j<n;j++)
{
if(sz[i][j]>exg[i])
exg[i]=sz[i][j];
}
}//初始化
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
sl[j]=inf;
while(1)
{
for(int j=0;j<n;j++)
vg[j]=vb[j]=false;
if(dfs(i))
break;
int zx=inf;
for(int j=0;j<n;j++)
{
if(!vb[j]&&sl[j]<zx)
zx=sl[j];//寻找最小下降值
}
for(int j=0;j<n;j++)
{
if(vg[j])
exg[j]-=zx;
if(vb[j])
exb[j]+=zx;
else //更新最小下降值
sl[j]-=zx;
}
}
}
}
网络流
最大流
增广路算法:每次找一条从源点到汇点的路径,以这条路经上的容量最小值为流量,进行增广。
但这样会出错,例如:
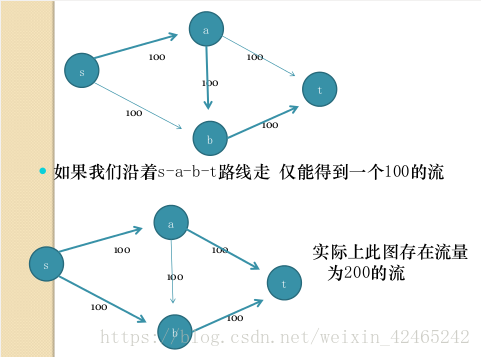
问题出在过早地认为边a → b上流量不为0,因而“封锁”了流量继续增大的可能。
一个改进的思路:应能够修改已建立的流网络,使得“不合理”的流量被删掉。
一种实现:对上次dfs时找到的流量路径上的边,添加一条“反向”边,反向边上的容量等于上次dfs时找到的该边上的流量,然后再利用“反向”的容量和其他边上剩余的容量寻找路径。
这就是通过反向边,来修改之前错误的决策。
这个思路是很常用的。
暴力算法:每次任意寻找一条增广路。
但有这样一个问题:
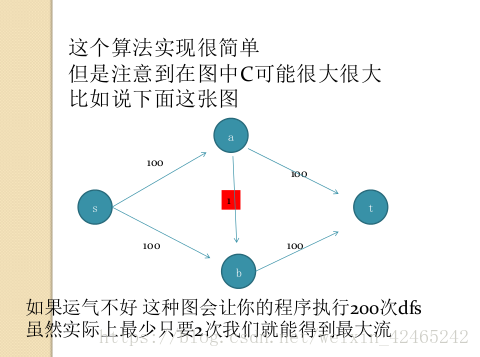
如何避免上述的情况发生?
在每次增广的时候,选择从源到汇的具有最少边数的增广路径,即不是通过dfs寻找增广路径,而是通过bfs寻找增广路径。
这就是EK 最短增广路算法。
这种算法的复杂度上限为\(O(nm^2)\)。
证明略。
但这样还是太慢。
dinic算法:
可以发现,EK算法主要慢在增广路的寻找上。
考虑优化这个过程。
每次,求出源点到每个点的距离。
建出分层图(即只保留距离为k指向k+1的边)。
在分层图上找增广路,就很快了。
复杂度分析:
因为每次bfs,都说明s~t的最短路长度增加了1。
所以bfs最多进行n次。
增广时可能遇到废边,只要把废边忽略就行了(当前弧优化)。
每一轮,废边只会忽略1次。
除此之外,找增广路就是\(O(n)\)的了。
所以复杂度为\(O(n^2m)\)
代码:
#include <stdio.h>
#define MN 10000
#define MM 100000
int fr[MN],ne[MM*2],inf=99999999;
int v[MM*2],w[MM*2],bs=0;
int dl[MN],S,T,jl[MN],N;
int dy[MN];
bool bk[MN];
void add(int a,int b,int c)
{
v[bs]=b;
w[bs]=c;
ne[bs]=fr[a];
fr[a]=bs;
bs+=1;
}
void addb(int a,int b,int c)
{
add(a,b,c);
add(b,a,0);//反向边
}
bool bfs()//bfs求距离标号
{
for(int i=0;i<N;i++)
bk[i]=false;
int he=0,ta=1;
bool rtn=false;
dl[0]=S;
while(he<ta)
{
int u=dl[he];
if(u==T)
rtn=true;
for(int i=fr[u];i!=-1;i=ne[i])
{
if(w[i]>0&&!bk[v[i]])
{
bk[v[i]]=true;
jl[v[i]]=jl[u]+1;
dl[ta++]=v[i];
}
}
he+=1;
}
return rtn;
}
int dfs(int u,int z)
{
if(u==T)
return z;
for(int &i=dy[u];i!=-1;i=ne[i])//当前弧优化
{
if(w[i]>0&&jl[v[i]]==jl[u]+1)//保证时最短路
{
int rt=dfs(v[i],w[i]<z?w[i]:z);
if(rt!=-1)
{
w[i]-=rt;
w[i^1]+=rt;//反向边
return rt;
}
}
}
return -1;
}
int dinic()
{
int he=0;
while(bfs())
{
for(int i=0;i<N;i++)
dy[i]=fr[i];
while(1)
{
int rt=dfs(S,inf);
if(rt==-1)
break;
he+=rt;
}
}
return he;
}
最小割
给定一个图,删去容量之和最小的边,使s到t不连通。
定理:最大流最小割定量: 在任何的网络中,最大流的值等于最小割的容量。
所以只要跑最大流即可。
构造方法:构造最小割的解(即割掉哪些边):
对残量网络进行bfs,设能够到达的集合为S,不够到达的集合为T (遍历时考虑反向边),
则从S指向T的边被割掉。
用此方法也能构造二分图的最大独立集。
平面图的最小割等于对偶图的最短路,路径中相邻两个面的分界边的最小边就是割掉的边。
最小割树
通过预处理,快速查询任意两点的最小割。
使用分治,每次在集合中任选S和T,然后求S和T的最小割,在S和T间连一条权值为最小割容量的边,将最小割形成的两个集合继续分治。
然后,任意两点间的最小割就是这两点在最小割树上的路径中权值最小的边对应的最小割。
费用流
这个和最大流的EK算法很像,就是以费用为边权,找最短路。
反向边的费用是正向边的相反数。
由于有负权边,使用SPFA。
循环流
(最大费用循环流)
可以这样理解:源点和汇点是同一点,这样费用流的最长路其实就是环路
为了费用最大,每次都应该找一个正环,进行增广。
解决二分图问题
匹配:
从源点向每个X部节点连容量为1的边,从每个Y部节点向汇点连容量为1的边,跑最大流即可。
连有向边。
解决最大独立集的构造问题:
按照上述方法建图,求最小割(二分图中原来的边容量为inf,其余为1)。
则没被割掉的边对应的点就在最大独立集中,其它的点在最小顶点覆盖中。
建模思想
结点上有流量限制
将点拆成入点和出点,入点连入边,出点连出边,这两个点之间的边容量为点权。
最小路径覆盖问题
对于一条路径,起点的入度为0,终点的出度为0,中间节点的出入度都为1。
每一个点最多只能有1个后继,同时每一个点最多只能有1个前驱。
假如我们选择了一条边(u,v),也就等价于把前驱u和后继v匹配上了。这样前驱u和后继v就不能和其他节点匹配。
利用这个我们可以这样来构图
将每一个点拆分成2个,分别表示它作为前驱节点和后继节点。将所有的前驱节点作为A部,所有后继节点作为B部。
接下来进行连边,若原图中存在一条边(u,v),则连接A部的u和B部的v。
在这个上面做一个最大二分匹配
这样在匹配结束的时候,我们就可以直接通过匹配的情况来确定选中的路径
方法如下:
从一个点开始,走到他匹配的Y部,再移回X部,直到没有匹配的Y部,就找到了一条路径。
费用随流量增长速度单调
将流量差分,把这条边拆开,每条边的流量为差分后的流量。
上下界网络流
有2种方法:
方法一:
将每条边上的流都减去其最小流量,这样就没有了最小流量限制,但是,这样不满足流量平衡,所以,在流量不平衡的时候,使用附加的源和附加的汇调整流量,使流量平衡。
在附加源汇后的图上跑最大流,若附加边都流满,则原问题有可行解,否则原问题无解。
在删除附加边后的残量网络上正向跑最大流,得到原图的最大流。
在删除附加边后的残量网络上反向跑最大流,消去原来的流,得到原图的最小流。
方法二:
将每个点拆成两个点,入点连入边,出点连出边,然后入点连一条到汇点的边,源点连一条到出点的边。
这样细节较少。
最大权闭合子图
最大权闭合子图指选择u,则u依赖的都要选。
增设一个超级源点和一个超级汇点,(1->n)的点中,当点权为正时,从源点向该点连一条权值为点权大小的边,当点权为负时,从该点连一条权值大小为它的绝对值的边连向汇点。
这种问题一般都是对于(u,v),如果选择u必须选择v,对(u,v)连一条容量为inf的边。
求最小割,割掉了到源点的边说明没选这个点,割掉了到汇点的边说明选了这个点。
例题
技巧总结
就是用流量来表示状态,状态转移就是对流连边,调整流量,对状态进行转移。
流量的价值和对流量的限制通过加边来实现。
要满足状态转移时流量总和不变,如果改变就要连接源点,连接汇点,强制调整流量。
一定要考虑所有可能的流,考虑能否流出不合法状态。
在图扩大时可以在残量网络上增广。
也可以对源点添加必须流满的边,分解流量后,进行匹配(就是建一个二分图)。
按照题目的描述,以及题目中量的转变关系,进行建图。
就是把量变成流。
分配方面就是建一个二分图。
如果有若干个可选,每个会给两个变量+1,每个变量有限制,可以建出二分图,使用最大流。
举例
餐巾计划问题:
一个餐厅在相继的 N天里,每天需用的餐巾数不尽相同。假设第 i 天需要 r_i块餐巾( i=1,2,...,N)。
餐厅可以购买新的餐巾,每块餐巾的费用为 p 分;或者把旧餐巾送到快洗部,洗一块需 m 天,其费用为 f 分;
或者送到慢洗部,洗一块需 n 天(n>m),其费用为s分。
每天结束时,餐厅必须决定将多少块脏的餐巾送到快洗部,多少块餐巾送到慢洗部,以及多少块保存起来延期送洗。
但是每天洗好的餐巾和购买的新餐巾数之和,要满足当天的需求量。
设计一个算法,为餐厅合理地安排好 N天中餐巾使用计划,使总的花费最小。编程找出一个最佳餐巾使用计划。
分析:
本题状态显然为餐巾数,所以,以餐巾数作为流量。
分析每天的过程:
- 接受洗部运来的餐巾。
- 将ri条餐巾送走。由于是送走,所以向汇点连边。
- 接受送来的旧餐巾,由于是送来,所以向源点连边。
- 将这些旧餐巾一部分送到快洗部,一部分送到慢洗部。
因为这些送走要求都要满足,所以求最大流。
其实就是有上下界的费用流问题。
方格取数问题,骑士共存问题
这两道都是二分图(带权)最大独立集问题,使用最小割。
由于人类对自然资源的消耗,人们意识到大约在 2300 年之后,地球就不能再居住了。
于是在月球上建立了新的绿地,以便在需要时移民。令人意想不到的是,2177 年冬由于未知的原因,地球环境发生了连锁崩溃,
人类必须在最短的时间内迁往月球。
现有 n 个太空站位于地球与月球之间,且有 m 艘公共交通太空船在其间来回穿梭。每个太空站可容纳无限多的人,
而每艘太空船 i 只可容纳 H[i]个人。每艘太空船将周期性地停靠一系列的太空站,
例如:(1,3,4)表示该太空船将周期性地停靠太空站 134134134…。每一艘太空船从一个太空站驶往任一太空站耗时均为 1。
人们只能在太空船停靠太空站(或月球、地球)时上、下船。
初始时所有人全在地球上,太空船全在初始站。试设计一个算法,找出让所有人尽快地全部转移到月球上的运输方案。
对于给定的太空船的信息,找到让所有人尽快地全部转移到月球上的运输方案。
同样,用流量表示状态。
状态就是每个太空站的人数。
由于总人数不变,所以满足流量平衡。
可以假设,每次太空船到站后,所有人都下船,然后再上船。
这样,太空船就只起到了转移人的作用,就相当于图中的边。
我们从小到大枚举结果,进行建图,判断最大流是否等于总人数。
由于图每次只有扩大,所以无需重新跑dinic,只需再残量网络上继续跑即可。
代码:
#include <stdio.h>
#define MN 10000
#define MM 100000
int fr[MN],ne[MM*2],inf=99999999;
int v[MM*2],w[MM*2],bs=0;
int dl[MN],S,T,jl[MN],N;
int dy[MN];
bool bk[MN];
void add(int a,int b,int c)
{
v[bs]=b;
w[bs]=c;
ne[bs]=fr[a];
fr[a]=bs;
bs+=1;
}
void addb(int a,int b,int c)
{
add(a,b,c);
add(b,a,0);
}
bool bfs()
{
for(int i=0;i<N;i++)
bk[i]=false;
int he=0,ta=1;
bool rtn=false;
dl[0]=S;
while(he<ta)
{
int u=dl[he];
if(u==T)
rtn=true;
for(int i=fr[u];i!=-1;i=ne[i])
{
if(w[i]>0&&!bk[v[i]])
{
bk[v[i]]=true;
jl[v[i]]=jl[u]+1;
dl[ta++]=v[i];
}
}
he+=1;
}
return rtn;
}
int dfs(int u,int z)
{
if(u==T)
return z;
for(int &i=dy[u];i!=-1;i=ne[i])
{
if(w[i]>0&&jl[v[i]]==jl[u]+1)
{
int rt=dfs(v[i],w[i]<z?w[i]:z);
if(rt!=-1)
{
w[i]-=rt;
w[i^1]+=rt;
return rt;
}
}
}
return -1;
}
int dinic()
{
int he=0;
while(bfs())
{
for(int i=0;i<N;i++)
dy[i]=fr[i];
while(1)
{
int rt=dfs(S,inf);
if(rt==-1)
break;
he+=rt;
}
}
return he;
}
int fa[50];
int getv(int x)
{
if(fa[x]==x)
return x;
fa[x]=getv(fa[x]);
return fa[x];
}
void heb(int x,int y)
{
x=getv(x);
y=getv(y);
if(x!=y)
fa[x]=y;
}
int sz[50][50],sl[50];
int wz[50],h[50];
int main()
{
int n,m,k;
scanf("%d%d%d",&n,&m,&k);
for(int i=0;i<=n+1;i++)
fa[i]=i;
for(int i=0;i<m;i++)
{
scanf("%d%d",&h[i],&sl[i]);
for(int j=0;j<sl[i];j++)
{
scanf("%d",&sz[i][j]);
if(sz[i][j]==-1)
sz[i][j]=n+1;
}
for(int j=1;j<sl[i];j++)
heb(sz[i][j-1],sz[i][j]);
}
if(getv(0)!=getv(n+1))
printf("0");
else
{
int liu=0;
fr[0]=fr[1]=-1;
N=1,S=0;
addb(0,1,k);
for(int t=0;1;t++)
{
for(int i=N;i<=N+n+2;i++)
fr[i]=-1;
if(t>0)
{
for(int i=0;i<m;i++)
{
addb(N-(n+3)+sz[i][wz[i]],N+sz[i][(wz[i]+1)%sl[i]],h[i]);
wz[i]=(wz[i]+1)%sl[i];
}
for(int i=0;i<=n+1;i++)
addb(N-(n+3)+i,N+i,inf);
}
N+=n+2;
T=N;
addb(N-1,T,k);
N+=1;
liu+=dinic();
if(liu==k)
{
printf("%d",t);
break;
}
}
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号