【trick小记】树状数组上倍增

以前都是写 zz 的双 \(\log\) 的树状数组上二分，今天来学一下单 \(\log\) 的树状数组上倍增。

解决问题

现在有两种操作；

• 插入一个数 \(x\)
• 查询排名为 \(k\) 的数

可以使用树状数组，以数值作为树状数组的下标（如果需要离散化就先离散化），插入一个数就是一次修改操作，我们考虑查询操作。

朴素的思路就是二分这个数，进行判断，复杂度是 \(\mathcal O(\log^2n)\)（其中 \(n\) 为值域范围），在随机数据跑的还是比较快的，但是复杂度还不够理想，考虑 \(\mathcal O(\log n)\) 的做法。

我们先来看一看树状数组的原理图。（图片来源网络）

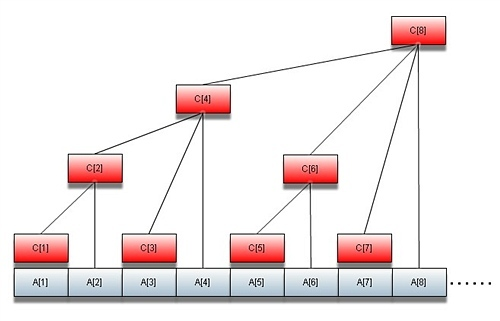
可以发现 $$C_i=\sum_{j=i-lowbit(i)+1}^{i}A_j$$
考虑倍增，每次跳 \(2^{\log n},2^{\log n-1},\cdots,2^1,2^0\) 的距离寻找答案。

int kth(int k)
{
	int l=0,tot=0,x,y;
	for(int i=log(n);i>=0;--i)
	{
		x=l+(1<<i);
		if(x>n)continue;
		y=tot+c[x];
		if(y<k)l=x,tot=y;
	}
	return l+1;
}

这样的话就完美利用了树状数组的特性，通过倍增在 \(\mathcal O(\log n)\) 的时间内求出了第 \(k\) 小的数。