树的直径

一、定义

直径的定义：不经过同一个点两次的最长链。

树的直径其实就是树上最长的路径。

二、直径的性质

1.从任意一个点出发，能到达的最远点一定是某条直径的端点

例题： [ABC428E] Farthest Vertex

由性质1可得，距离一个点最远的点一定在树的直径上。

先2次dfs求出直径，然后对于每一个点，求出它和直径两条端点的距离（通过$ LCA $）取最大值即可。

code

#include <bits/stdc++.h>
#define int long long
#define ll long long
#define ull unsigned long long
#define inf 1e15
#define eps 1e-4
#define endl "\n"
#define il inline
using namespace std;
const int N=1e6+5,M=105;
const int mod=998244353;
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-') f=-1;
        ch=getchar();
    }
    while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
    return x*f;
}
int maxn=0,id,id2,l,r;
int n,dep[N],f[N];
int pl[N][25];
vector<int>E[N];
inline void init(int x,int fa){
    dep[x]=dep[fa]+1;
    if(dep[x]>maxn) maxn=dep[x],id=x;
    else if(dep[x]==maxn && id<x) id=x;
    for(auto to : E[x]){
        if(to==fa) continue;
        init(to,x);
    }
    return ;
}
inline void dfs(int x,int fa){
	dep[x]=dep[fa]+1;
	pl[x][0]=fa;
	for(int k=1;pl[x][k-1];k++) pl[x][k]=pl[pl[x][k-1]][k-1];
	for(auto to : E[x]){
		if(to==fa) continue;
		dfs(to,x);
	}
	return ;
}
inline int LCA(int x,int y){
	if(dep[x]<dep[y]) swap(x,y);
	for(int k=20;k>=0;k--){
		if(dep[pl[x][k]]<dep[y]) continue;
		x=pl[x][k];
	}
	if(x==y) return x;
	for(int k=20;k>=0;k--){
		if(pl[x][k]==pl[y][k]) continue;
		x=pl[x][k],y=pl[y][k];
	}
	return pl[x][0];
}
signed main(){
    n=read();
    for(int i=1,u,v;i<n;i++){
        u=read(),v=read();
        E[u].push_back(v);
        E[v].push_back(u);
    }
    init(1,0);
    l=id;id2=id;
    id=0;maxn=0;
    init(id2,0);
    r=id;
    dfs(1,0);
    f[l]=r,f[r]=l;
    for(int i=1;i<=n;i++){
    	if(i==l || i==r) continue;
    	int x=LCA(i,l),y=LCA(i,r);
    	int aa=dep[i]+dep[l]-dep[x]*2;
    	int bb=dep[i]+dep[r]-dep[y]*2;
    	if(aa>bb) f[i]=l;
    	else if(aa<bb) f[i]=r;
    	else f[i]=max(l,r);
	}
    for(int i=1;i<=n;i++) printf("%lld\n",f[i]);
    return 0;
}

2.所有直径共中点

这里所说的中点，并不一定指的是一个结点，它也有可能在边上。

所有直径的中点一定重合。

3.所有直径在公共部分以外的部分相等

由于所有直径共中点，所以一定有一个公共部分。

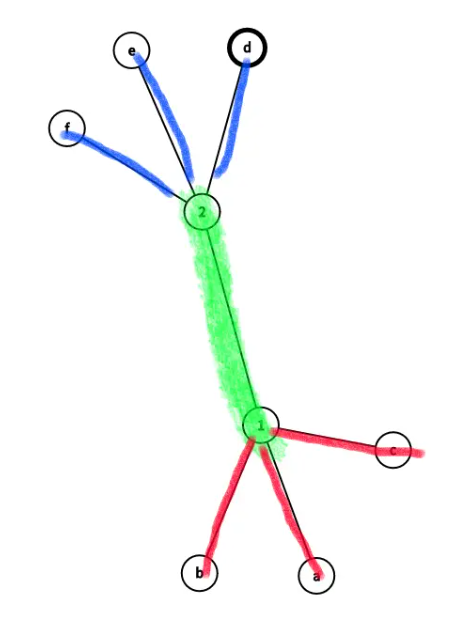
如下图，三段红色部分和三段蓝色部分显然相等。

4.新直径有关

用一条边 \({(u, v)}\) 将两棵树 \({T_1}\)，\({T_2}\) 连接，合成的新树 \(T\) 的所有直径都只有两种情况：

• 不经过 \({(u, v)}\)，仍为原来 \({T_1}\) 的某条直径，或仍为原来 \({T_2}\) 的某条直径。

• 经过 \({(u, v)}\)，两个端点分别落在 \({T_1}\) 和 \({T_2}\) 中，且分别是 \({T_1}\)，\({T_2}\) 中某条直径的某个端点。

所以两颗树，直径分别为 $ (u,v) $ 和 $ (x,y) $ ，⽤⼀条边将两树连起来，新树的直径⼀定是 $ (u,v),(x,y),(u,x),(u,y),(v,x),(v,y) $之一。

退化版结论：树直径 $ (u,v) $ ，加上一个点 $ w $ ，直径一定是 $ (u,v),(u,w),(v,w) $ 之一。