树链剖分

一、定义

树链剖分的本质就是把树上对于链、子树的操作，转化为 \(dfs\) 序列上的操作（用线段树等数据结构维护）。

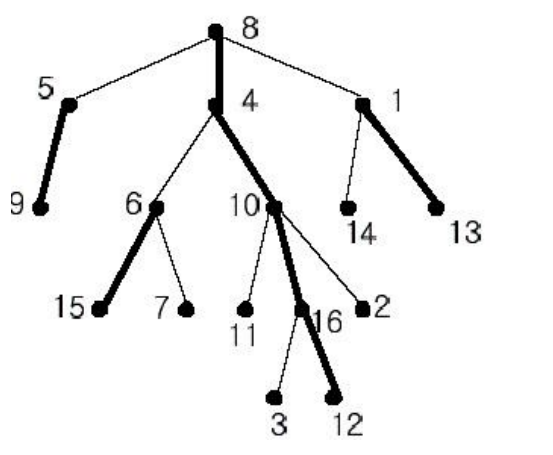
定义重儿子为每个节点儿子中子树大小最大的那个（如果有多个则任取一个）。

父亲连向重儿子的边称为重边，其他边称为轻边，重边组成的链称为重链。

\(dfs\) 时先搜重儿子，重链上的点的 \(dfs\) 序就是连续的。

关键性质：任何一个点到根节点的路径上至多有 $ log n $ 条轻边 ，也就把路径分成了 $ log n $条重链，对应着 $ dfs $ 序列上 $ log n $ 段连续区间 。

所以，树链剖分从任意节点跳到根节点的复杂度为 $ O(log n) $。

二、基础操作

1、预处理

求出\(dfs\)序和重链。

void dfs1(int x,int fa){
    dep[x]=dep[fa]+1;
    f[x]=fa,siz[x]=1;
    for(auto to : E[x]){
        if(to==fa) continue;
        dfs1(to,x);
        siz[x]+=siz[to];
        if(siz[to]>siz[hson[x]]) hson[x]=to;
    }
    return ;
}
void dfs2(int x,int tp){
    dfn[++cnt]=x,pos[x]=cnt;
    top[x]=tp;
    if(hson[x]) dfs2(hson[x],tp);
    for(auto to : E[x]){
        if(to==f[x]) continue;
        if(to==hson[x]) continue;
        dfs2(to,to);
    }
    return ;
}

2、树剖求LCA

求两个点的 \(LCA\) 。

当两个点不在一条重链上时，每次让链头深度大的那个点向上跳一条重链，直到两个点在同一条重链上为止。

然后返回深度较浅的那个点。

inline int LCA(int x,int y){
    while(top[x]!=top[y]){
        if(dep[top[x]]>dep[top[y]]) x=f[top[x]];
        else y=f[top[y]];
    }
    if(dep[x]<dep[y]) return x;
    else return y;
}

3、树链操作

过程与求 $ LCA $ 类似，一般用线段树维护

以树链加和树链求和为例。

树链加：

当两个点不在一条重链上时，每次让链头深度大的那个点到链头这段区间加，同时向上跳一条重链，直到两个点在同一条重链上为止。

然后对这两个点之间的$ dfs $序列区间加。

void modify(int x,int y,int v){
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        T.interval_change(1,1,n,pos[top[x]],pos[x],v);
        x=f[top[x]];
    }
    if(dep[x]>dep[y]) swap(x,y);
    T.interval_change(1,1,n,pos[x],pos[y],v);
    return ;
}

树链求和：

当两个点不在一条重链上时，每次让链头深度大的那个点到链头这段区间求和，同时向上跳一条重链，直到两个点在同一条重链上为止。

然后对这两个点之间的$ dfs $序列区间求和。

int qry(int x,int y){
    int res=0;
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        res+=T.query(1,1,n,pos[top[x]],pos[x]);
        x=f[top[x]];
    }
    if(dep[x]>dep[y]) swap(x,y);
    res+=T.query(1,1,n,pos[x],pos[y]);
    return res;
}

4、子树操作

重要性质：子树在\(dfs\)序上是连续的一段。

直接在\(dfs\)序列上操作即可。

子树加：

void sub_modify(int x,int v){
    T.interval_change(1,1,n,pos[x],pos[x]+siz[x]-1,v);
    return ;
}

子树求和：

int sub_qry(int x){
    return T.query(1,1,n,pos[x],pos[x]+siz[x]-1)%mod;
}

5、处理边权

将每条边的边权当做深度更深的那个点的点权即可。

注意跳到 $ LCA $ 所在的链时，不要把 $ LCA $ 也算进去（它代表上面那条边的边权）。

6、树上移动

树剖还可以模拟在树上移动。

如从$ u $ 点向 $ v $ 点方向移动 $ t $ 步，步数够用就到 $ v $ 点停止，不够就沿最短路径走到哪算哪。

令 $ dis(u,v) $ 表示 $ u $ 到 $ v $ 的距离。

则分一下三种情况讨论。

1. $ dis(u,v)≤t $ .

直接跳到 $ v $ 点即可。

2. $ dis(u,LCA)≥t $ .

令 $ u $ 点不断向上跳重链，

如果当前链头到当前的点的距离等于 $ t $，返回链头；

如果当前链头到当前的点的距离大于 $ t $，说明答案在当前链上，直接返回 $ dfn[pos[x]-t+1] $ ;

如果当前链头到当前的点的距离大于 $ t $，向上跳一条重链，继续操作。

3. $ dis(u,LCA)<t<dis(u,v) $ .

同理第2种情况，让 $ v $ 向上跳 $ dis(u,v)-t $ 步即可。