河南萌新联赛2025第（五）场：信息工程大学”题解

虽然是第一次出题，但是体验还是很不错的，就是ak的太多了验题的时候感觉难度正常，但是实际偏差较大，不知道是全来炸鱼还是河南省acm实力日渐增强，这都是我所希望的
河南萌新联赛2025第（五）场

简单
A,B,F,G,C

A题，依题意模拟即可，从0开始试错只会错2次

B题，只有最大值和最小值不会被删，剩下的只会是这两个数

F题，依题意模拟即可

G题，拆解行列式可发现是斐波那契数列，之后找规律即可

C题，对顶堆模板题

中等
E，I，K，H，K

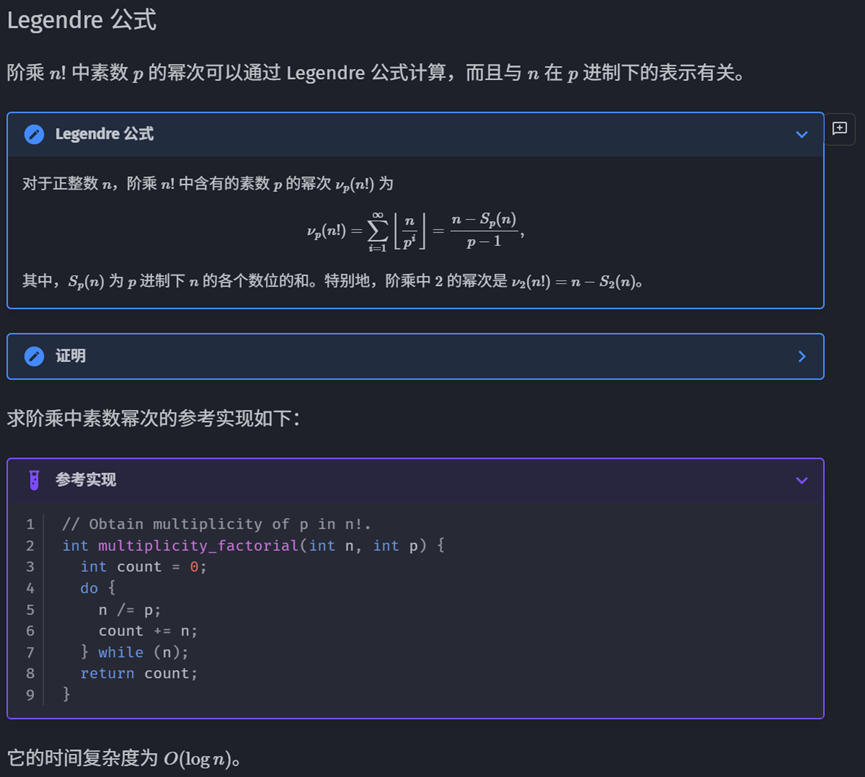
E题有一个经典的数论结论，Legendre公式：n!中p因子的个数可计算，故分解k求结果取最小即可

I题，本题要对每次询问的两个点查询包含这两个点和根节点的最小子树，可以先dfs一次预处理出每个点x到根节点的路径上节点的权重和d_x，对于一次对点x和y的询问，先求出x和y的lca，设为点z，运用容斥原理，在 d_x+d_y中，从根节点到点z路径上的点被计算了两次，那么答案就是d_x+d_y-d_z
如果用倍增法求lca，预处理O(n)，每次查询O(logn)，总时间复杂度O(n+qlogn)

K题正向bfs会超时，只能逆向模拟：
从终点 (x, y) 倒着走到起点 (sx, sy)。
不失一般性，假设 x ≥ y 且 x > 0。若 x < y，交换 x 和 y，以及交换 sx 和 sy。假设 x > 0，因 x = y = 0 情况可特判。
注：可交换原因是 x 与 y 无序，计算 max (x, y)、操作 (x + m, y) 或 (x, y + m)（给其中一个数加 m ）均无序，故 (x, y) 与 (y, x) 等价，答案相同；若 x < y ，点会变换到直线 y = x 镜像位置 (y, x) 。
从 (x, y) 倒退一步，需明确上一步位置与执行操作，分以下情况：
执行操作一（横坐标相关：横坐标加横坐标 / 横坐标加纵坐标 ）
上一步横坐标乘 2：上一步在 (x/2, y) ，前提为 x 是偶数且 max (x/2, y) = x/2（即 x ≥ 2y ）。
上一步横坐标加 y：上一步在 (x - y, y) ，前提为 max (x - y, y) = y（即 x ≤ 2y ）。
执行操作二（纵坐标相关：纵坐标加纵坐标 / 纵坐标加横坐标 ，类似推导 ）
上一步在 (x, y/2) ：前提为 y 是偶数且 max (x, y/2) = y/2（即 x ≤ y/2 ），结合 x ≥ y 假设，得 y ≤ y/2 ，仅 y = 0 时成立（不考虑负数 ）；代入 y ≤ x ≤ y/2 ，得 0 ≤ x ≤ 0 即 x = 0 ，与 x > 0 矛盾，无需考虑。
上一步在 (x, y - x) ：因 y - x ≤ 0 且不考虑负数，仅 x = y 时可操作，此时 x = y > 0 。
倒退一步的方法总结
若 x = y ：
当 sy > 0 ，只能把 x 变 0（把 y 变 0 无法回起点 ）。
当 sx > 0 ，只能把 y 变 0（把 x 变 0 无法回起点 ）。
无需判断 sx = sy = 0 ，x 或 y 减半会变奇数，会返回 -1 。
若 x > y ，此时仅执行操作一：
若 x > 2y ，把 x 减半 。
若 x < 2y ，把 x 减少 y 。
若 x = 2y ，二者效果一样，都会把 x 变成 y 。
按照上述规则模拟，每倒退一步，把答案加一。即若未返回 -1 ，就按规则逐步回退计算 。

H题，数学题，化简发现是斐波那契数列，用矩阵快速幂加速即可

K题，二分答案，用贪心和模拟来check，显然集中力量打一只对于战士来说是最佳选择（题名误导性有些强了。。。）

困难
D，J

D题，为了解决“所有非空子集异或和的中位数”问题，我们需高效处理大规模子集（共 (2^N - 1) 个）。核心思路是利用线性基和异或性质避免枚举所有子集。在线性基内第一位置1其他位置0即可满足，本题数据较弱比较容易放过

J题，在hard版本中每次查询没有了点数量的限制，如果依然使用容斥原理，每次查询O(2^k logn)会超时，可以把每次待查询的点按照dfs序排序，然后从小到大逐个点处理，假设z和ans分别是已经处理过的点的lca和包含这处理过的点和根节点的最小子树的权重，当处理下一个点y时，把ans加上d_y-d_(lca(z,y))，并将z更新为lca(z,y)即可
时间复杂度：预处理O(n),每次查询需要排序和求lca，总时间复杂度O(n+∑k*log∑k)