2025icpc郑州省赛补题
I
被这题莫名其妙卡了好久,队友交了两发py代码第一发tle第二发ac,中间我没理解他做法就按他意思改c++,结果有个小细节没注意就一直wa了好多发
做法就是一个凸包问题,维护上凸包斜率单调栈即可
点击查看代码
#include<bits/stdc++.h>
#define x first
#define y second
#define pdd pair<double,double>
#define rep(a,b,c) for(int a = b;a<=c;++a)
using namespace std;
int n,cnt = 0;
const int N = 2e5+4;
pdd p[N],d[N];
bool cmp(pdd a,pdd b){
if(a.x == b.x)return a.y>b.y;
return a.x<b.x;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
rep(i,1,n){
cin>>p[i].x>>p[i].y;
}
sort(p+1,p+1+n,cmp);
d[++cnt] = p[1];
rep(i,2,n){
while(p[i].x == d[cnt].x) continue;
if(cnt == 1){
d[++cnt] = p[i];
continue;
}
double k1 = (p[i].y-d[cnt].y)/(p[i].x-d[cnt].x);
double k2 = (d[cnt].y-d[cnt-1].y)/(d[cnt].x-d[cnt-1].x);
while(k1>k2){
--cnt;
if(cnt == 1)break;
k1 = (p[i].y-d[cnt].y)/(p[i].x-d[cnt].x);
k2 = (d[cnt].y-d[cnt-1].y)/(d[cnt].x-d[cnt-1].x);
}
d[++cnt] = p[i];
}
double ans = 0;
rep(i,1,cnt-1){
ans += (d[i+1].x-d[i].x)*(d[i+1].y+d[i].y)/2;
}
cout<<ans;
}
C
一开始看了f题感觉要用并查集,后来看这题自然想到并查集了,写了个o(nlonn)的挂了,后来被i题卡着一直没写,结果刚比完就想到可以优化到o(n),不用并查集。
先dfs一遍图x得到每个点对应的连通块(标记成这个连通块第一个被搜到的点)
然后dfs搜图y对应的连通块,用unordered_map存在这次搜索的图y连通块里,对应在图x的每个连通块里有多少个点,很容易想到如果有一个集合s,|s| = k,s中的所有点在图x和图y中都是在同一个连通块中,那么其中任意两点都是符合要求点对,集合s贡献(k-1)*k/2;对图y的dfs能完成所有这样s的统计。
使用记忆化搜索,时间复杂度o(m1+m2+n).
(链式向前星双向图要开4e6)
点击查看代码
#include<bits/stdc++.h>
#define x first
#define y second
#define pdd pair<double,double>
#define rep(a,b,c) for(int a = b;a<=c;++a)
using namespace std;
typedef long long ll;
const int N = 4e6+3;
int n,m1,m2,cnt1,cnt2,sta;
int h1[N],h2[N],s[N],vis[N];
map<int,int> mp;
struct {
int to,next;
}e1[N],e2[N];
void init(){
for(int i = 0;i<N;++i){
h1[i] = -1;h2[i] = -1;
}
rep(i,0,N-1){
e1[i].next = -1;e2[i].next = -1;
}
cnt1 = 0;cnt2 = 0;
}
void ade1(int u,int v){
e1[cnt1].to = v;
e1[cnt1].next = h1[u];
h1[u] = cnt1++;
}
void ade2(int u,int v){
e2[cnt2].to = v;
e2[cnt2].next = h2[u];
h2[u] = cnt2++;
}
void dfs1(int x){
s[x] = sta;
for(int i = h1[x];i!=-1;i = e1[i].next){
if(!s[e1[i].to])dfs1(e1[i].to);
}
}
void dfs2(int x){
vis[x] = 1;
mp[s[x]] += 1;
for(int i = h2[x];i!=-1;i = e2[i].next){
if(!vis[e2[i].to])dfs2(e2[i].to);
}
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m1>>m2;
init();
int u,v;
rep(i,1,m1){
cin>>u>>v;
ade1(u,v);ade1(v,u);
}
rep(i,1,m2){
cin>>u>>v;
ade2(u,v);ade2(v,u);
}
rep(i,1,n){
if(!s[i]){
sta = i;
dfs1(i);
}
}
ll ans = 0;
rep(i,1,n){
if(!vis[i]){
mp.clear();
dfs2(i);
for(auto i:mp){
//cout<<i.x<<' '<<i.y<<'\n';
ans += 1ll*i.y*(i.y-1)/2;
}
}
}
cout<<ans;
return 0;
}
D
队友很早就想到这本质上是一颗n个节点,深度最大为m,根为1的树有多少种的计数问题,但是我一开始没想到dp,最后被i题卡到就剩20分钟时我突然想到了dp状态设法,可惜没时间做了,出去一看想法跟题解大差不差
总之就是做一个3维dp,\(dp_{i,j,k}\)代表总共有j个点,深度为i,第i层节点个数为k的树总共有多少
转态转移的话遍历所有深度为i-1,节点为j-k个的树,设其第i-1层有t个节点,遍历所有t,在剩下n-(j-k)里选k个点接在这t个点上就完成了计数
\(dp_{i,j,k}\) = \(dp_{i,j,k}\)+\(dp_{i-1,j-k,t}\)\(\binom{n}{k}\)\(t^k\);
最后把所有深度不大于m的dp计数即可
总复杂度\(O(n^3m)\)
点击查看代码
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define lowbit(x) = ((x)& - (x))
#define rep(a,b,c) for(int a=b;a<=c;a++)
#define per(a,b,c) for(int a=b;a>=c;a--)
#define x first
#define y second
using namespace std;
typedef long long ll;
const int N = 103;
const ll mod = 1e9+7;
ll n,m;
ll c[N][N],fac[N][N];
ll dp[N][N][N];
void init(){
c[0][0] = 1;
rep(i,1,N-1){
c[i][0] = 1;
rep(j,1,i){
c[i][j] = (c[i-1][j]+c[i-1][j-1])%mod;
}
}
rep(i,1,101){
fac[i][0] = 1;
rep(j,1,101){
fac[i][j] = fac[i][j-1]*i%mod;
}
}
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
init();
dp[0][1][1] = 1;
rep(i,1,m){
rep(j,i+1,n){
rep(k,1,j-i){
rep(t,1,j-k-i+1){
dp[i][j][k] = (dp[i][j][k]+((dp[i-1][j-k][t]*c[n-j+k][k])%mod)*fac[t][k]%mod)%mod;
}
//cout<<i<<' '<<j<<' '<<k<<' '<<dp[i][j][k]<<'\n';
}
}
}
ll ans = 0;
rep(i,1,n){
ans = (ans + dp[m][n][i])%mod;
//cout<<dp[m][n][i]<<' ';
}
//cout<<c[3][2];
cout<<ans;
return 0;
}
F
赛时一看感觉很简单,但是又想不出来,一开始想的并查集,发现复杂度有问题,也闪过一瞬间lca的做法,但是没往下想,出来后恍然大悟,就是在维护lca同时维护路径最大时间戳
这里使用倍增法lca(tajan和树链刨分不太会用没想过维护时间戳)
建树时记录每条边的时间戳,令w[x][i]表示节点x到其第\(2^i\)个祖先路径上的最大时间戳,在dfs记录fa数组的同时可以记录w数组,w[x][i] = max(w[x][i-1],w[fa[x][i-1]][i-1]),这与倍增lca求fa数组的思路差不多
查询时可以一边求lca一边记录路上的最大时间戳,把每个点对的时间戳记录下来,时间i对应的点对数量设为a[i],对a[i]求前缀和就是答案
点击查看代码
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define lowbit(x) = ((x)& - (x))
#define rep(a,b,c) for(int a=b;a<=c;a++)
#define per(a,b,c) for(int a=b;a>=c;a--)
using namespace std;
typedef long long ll;
const int N = 1e5+4;
int n,m;
struct edge{
int to,tm;
};
int ans[N];
int dp[N],fa[N][18],w[N][18];
vector<edge> e[N];
void dfs(int x,int f,int v){
dp[x] = dp[f]+1;
fa[x][0] = f;
w[x][0] = v;
for(int i = 1;(1<<i) <= dp[x];i++){
fa[x][i] = fa[fa[x][i-1]][i-1];
w[x][i] = max(w[x][i-1],w[fa[x][i-1]][i-1]);
//if(x == 5)cout<<w[fa[x][i-1]][i-1]<<'\n';
}
for(auto &i:e[x]){
if(i.to!=f){
dfs(i.to,x,i.tm);
}
}
}
int lca(int x,int y){
int res = 0;
if(dp[x]<dp[y]) swap(x,y);
for(int i = 17;i>=0;--i){
if(dp[x]-(1<<i)>=dp[y]){
res = max(res,w[x][i]);
x = fa[x][i];
}
//if(x == y)cout<<'a';
if(x == y)return res;
}
for(int i = 17;i>=0;--i){
if(fa[x][i] != fa[y][i]){
res = max(res,max(w[x][i],w[y][i]));
//cout<<res<<'\n';
x = fa[x][i];y = fa[y][i];
}
}
res = max(res,max(w[x][0],w[y][0]));
return res;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
int u,v;
rep(i,1,n-1){
cin>>u>>v;
e[u].emplace_back(edge{v,i});
e[v].emplace_back(edge{u,i});
}
dfs(1,0,0);
rep(i,1,m){
cin>>u>>v;
ans[lca(u,v)]++;
}
rep(i,1,n-1){
//cout<<ans[i]<<' ';
ans[i] += ans[i-1];
}
//cout<<lca(1,3);
rep(i,1,n-1)cout<<ans[i]<<'\n';
return 0;
}
G
之前遇到过一道类似的题,知道卢卡斯定理可以快速判断组合数奇偶,但是对区间上的所有组合数判断就不太明白了,之前一直感觉数位dp,但是数位dp要考虑的有点多,不太会写,一看题解发现可以用高维前缀和才明白
卢卡斯定理:
设 $ p $ 为质数,$ n $ 和 $ k $ 为非负整数,且 $ n $ 和 $ k $ 的 $ p $ 进制表示为:
则卢卡斯定理断言:
\(
\binom{n}{k} \equiv \prod_{i=0}^{m} \binom{n_i}{k_i} \pmod{p},
\)
其中约定当 $ k_i > n_i $ 时 $ \binom{n_i}{k_i} = 0 $。
将p取2可以快速判断组合数奇偶
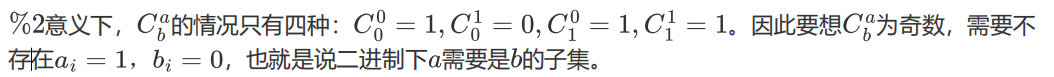
那么对所有奇数组合数计数的问题就转化成了子集和计数问题,这可以用高维前缀和解决,数据范围是1e6,约为\(2^{20}\),设N=20,复杂度为\(O(N2^N)\)
点击查看代码
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define lowbit(x) = ((x)& - (x))
#define rep(a,b,c) for(int a=b;a<=c;a++)
#define per(a,b,c) for(int a=b;a>=c;a--)
#define x first
#define y second
using namespace std;
typedef long long ll;
const int N = (1<<20);
int t;
ll l,r;
ll s[N];
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>t;
while(t--){
cin>>l>>r;
rep(i,0,N-1)s[i] = 0;
rep(i,l,r)s[i] = 1;
rep(i,0,19){
for(int j = 0;j<(1<<20);++j){
if((j>>i)&1)s[j] += s[j ^ (1<<i)];
}
}
ll ans = 0;
rep(i,l,r)ans+=s[i];
cout<<ans<<'\n';
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号