2025超越杯校赛总结

7题第四，只有3个金(为什么是5%)，因为罚时太多遗憾银首，去年新生赛也是银首，团体赛也是银，我是吸银体质吗？？？
这里记录每题的解法，赛时写过的题没存代码

A.奶龙大陆
要让第k小数恰为x，取一个极大值inf为1e18，数组b前k-1个取-inf，后n-k个取inf，第k个取x-a[k]即可，(注意开long long ，因为没开我wa了两发T_T)

B.简单博弈
可以把每堆石头单独看成一个博弈，把最经典的一堆石头轮流拿推广一下就能得到结论，后手胜当且仅当所有石头堆石头数都是偶数

C.奶龙的奇妙能量公式
n<=10，暴力遍历所有2^n-1种可能就好了

D.奶龙战斗
bfs，把敌人存到优先队列里，无路可走时拿出队列里最小一个敌人，如果能击败就从其位置接着bfs，直到无法击败队列里最小敌人而且无路可走时结束

E.队列进行中
把插入的数值和个数当成整体(c,x)放入队列中，弹出时整体弹出，并用快速幂计算乘积，同时维护队列里元素和。

F.奶龙的黄金芝士风暴全境探测
把a[i]>=x标记为1，a[i]<x记为-1，求前缀和,s[i]就是区间0-i里金奶酪块与蓝奶酪块数量差，如果有i<j且s[j]-s[i-1]>=0说明区间i-j里金奶酪数量>=蓝奶酪数量，也就是求前缀和s数组的逆序对，用数组数组求逆序对，由于有负数需要整体向右偏移，多测清空可以update(x,-1)，这题wa了好多发才过

G.奶龙的奇数区间
开始写了个错误解法一直以为是对的，导致浪费大量时间还没过题
正解：对于一个中心点i，区间权值对半径具有单调递增性，枚举每个中心点，二分半径找到使区间权值大于x的最小半径，所有取最小即是答案
考虑怎么快速求一个区间权值，对于区间右半部分预处理a[i]和i*a[i]前缀和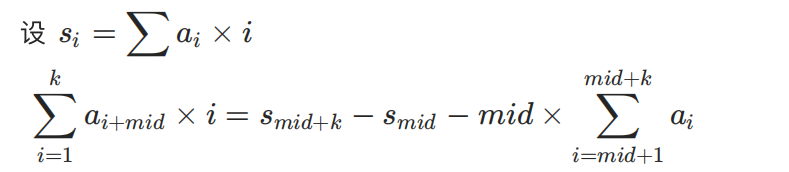

点击查看代码

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define lowbit(x) = ((x)& - (x))
#define rep(a,b,c) for(int a=b;a<=c;a++)
#define per(a,b,c) for(int a=b;a>=c;a--)
#define x first
#define y second
using namespace std;
typedef long long ll;
const ll inf = 1e18;
const int N = 1e6+4;
ll n,x;
ll a[N],s1[N],s2[N],t1[N],t2[N];

bool check(int t, int l){
    ll res = 0;
    res += s2[t+l-1]-s2[t-1]-(t-1)*(s1[t+l-1]-s1[t-1]);
    res += t2[t-l+1] - t2[t+1] - (n-t)*(t1[t-l+1] - t1[t+1]);
    res-=a[t];
    if(res>=x)return true;
    else return false;
}

ll solve(ll t){
    ll l = 1,r = min(t,n-t+1),mid;
    while(l<r){
        mid = (l+r)>>1;
        if(check(t,mid))r = mid;
        else l = mid + 1;
    }
    if(!check(t,l))return inf;
    else return l;
}

int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>x;
    rep(i,1,n)cin>>a[i];
    rep(i,1,n){
        s1[i] = s1[i-1]+a[i];
        s2[i] = s2[i-1]+i*a[i];
    }
    per(i,n,1){
        t1[i] = t1[i+1] + a[i];
        t2[i] = t2[i+1] + (n-i+1) * a[i];
    }
    ll ans = inf;
    rep(i,1,n){
        ans = min(ans,solve(i));
        //cout<<solve(i)<<' ';
    }
    if(ans == inf)cout<<-1;
    else cout<<ans*2-1;
    
	return 0;
}

H.隐秘的联系
⼀些数有且仅有⼀个公共质因⼦等价于这些数的gcd有且仅有⼀个质因⼦，在确定右区间的前提下随左区
间的扩张，区间gcd的质因⼦也将减少，所以可以先预处理每个数的质因⼦数量，枚举右端点，⼆分左端
点的区间（队友补的）

I.奶龙的数组
思考怎么求一个甜蜜度组合的后继，一个甜蜜度组合后继只有两种可能，设其中一种奶油的最大权值为a[i]，要么把a[i]换成a[i+1],要么加入一个a[i+1]，在优先队列中维护，输出前k个即可

点击查看代码

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define lowbit(x) = ((x)& - (x))
#define rep(a,b,c) for(int a=b;a<=c;a++)
#define per(a,b,c) for(int a=b;a>=c;a--)
using namespace std;
typedef long long ll;

struct node{
    ll s,ave,id,cnt;
    bool operator < (const node & x)const {
        return ave>x.ave;
    }
};
const int N = 1e6+3;
int n,k;
int a[N];
priority_queue<node> q;

int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>k;
    rep(i,1,n)cin>>a[i];
    sort(a+1,a+n+1);
    //cout<<a[1]<<'\n';
    q.emplace(node{a[1],a[1],1,1});
    node p,p2;
    while(k>0){
        p = q.top();q.pop();
        cout<<p.ave<<'\n';--k;
        if(p.id==n)continue;
        p2 = node{p.s+a[p.id+1],(p.s+a[p.id+1])/(p.cnt+1),p.id+1,p.cnt+1};
        q.emplace(p2);
        p2 = node{p.s-a[p.id]+a[p.id+1],(p.s-a[p.id]+a[p.id+1])/p.cnt,p.id+1,p.cnt};
        q.emplace(p2);
    }
	return 0;
}

J.奶龙的玩具乐园大冒险
设想有个超级源点连接每个神秘惊喜，对这个超级源点做迪杰斯特拉算法就能得到每个玩具点的能量，按其排序二分就能得到每个询问的答案

K.题目太长懒得写
签到输出yes就行

L.奶龙的数组
临时补的防ak的题，确实难

如果有两个包子第i个特征值相同，那么一定不能通过询问第i个特征值区分它们
用二进制数表示两个包子状态，如果两个包子第i个特征值相同那么第i位是1
预处理每两个包子间状态，同样用二进制数表示询问，询问第i个值第i位就是1
对于一个询问q，如果存在两个包子之间的状态x使q是x的子集(就是说q的每个为1的位在x的对应位上也是1)，
那么q一定不能区分这两个包子。
考虑如何判断一个q是某x的子集
做高维前缀和，m位二进制数是m维前缀和，把每个状态标1，对每个j使i是j的子集，s[i] 是所有s[j]的和
那么q能区分所有包子当且仅当s[q] == 0，遍历所有询问取询问最少并计数就得到答案

点击查看代码

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define lowbit(x) = ((x)& - (x))
#define rep(a,b,c) for(int a=b;a<=c;a++)
#define per(a,b,c) for(int a=b;a>=c;a--)
#define x first
#define y second
using namespace std;
typedef long long ll;

const int N = 2002;
int n , m;
int a[N][22];//t[(1<<20)+3];
ll s[(1<<20) + 3];


int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>m;
    rep(i,1,n){
        rep(j,1,m)cin>>a[i][j];
    }
    int p = 0;
    rep(i,1,n){
        rep(j,i+1,n){
            p = 0;
            rep(k,1,m){
                if(a[i][k] == a[j][k])p+=(1<<(k-1));
            }
            s[p] = 1;
        }
    }
    
    for(int i = 0;i<m;++i){
        for(int j = (1<<m)-1;j>=0;--j){
            if(!(j & (1 << i)))s[j] += s[(j ^ (1 << i))]; 
        }
    }
    int cnt = 0,mi = 100,ans = 0;
    rep(i,0,(1<<m)-1){
        if(s[i] == 0){
            int k = 0;cnt = 0;
            while((1<<k)<=i){
                if(i&(1<<k))++cnt;
                ++k;
            }
            if(cnt<mi){
                mi = cnt;ans = 1;
            }
            else if(cnt == mi)++ans;
        }
    }
    //rep(i,0,7)cout<<t[i]<<' ';cout<<'\n';
    //rep(i,0,7)cout<<s[i]<<' ';cout<<'\n';
    cout<<mi<<' '<<ans;
    
    
	return 0;
}