第三次作业

第三次作业

1.题目和问题：最大连续子数组和（最大子段和） 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n

例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20

2.代码如下：

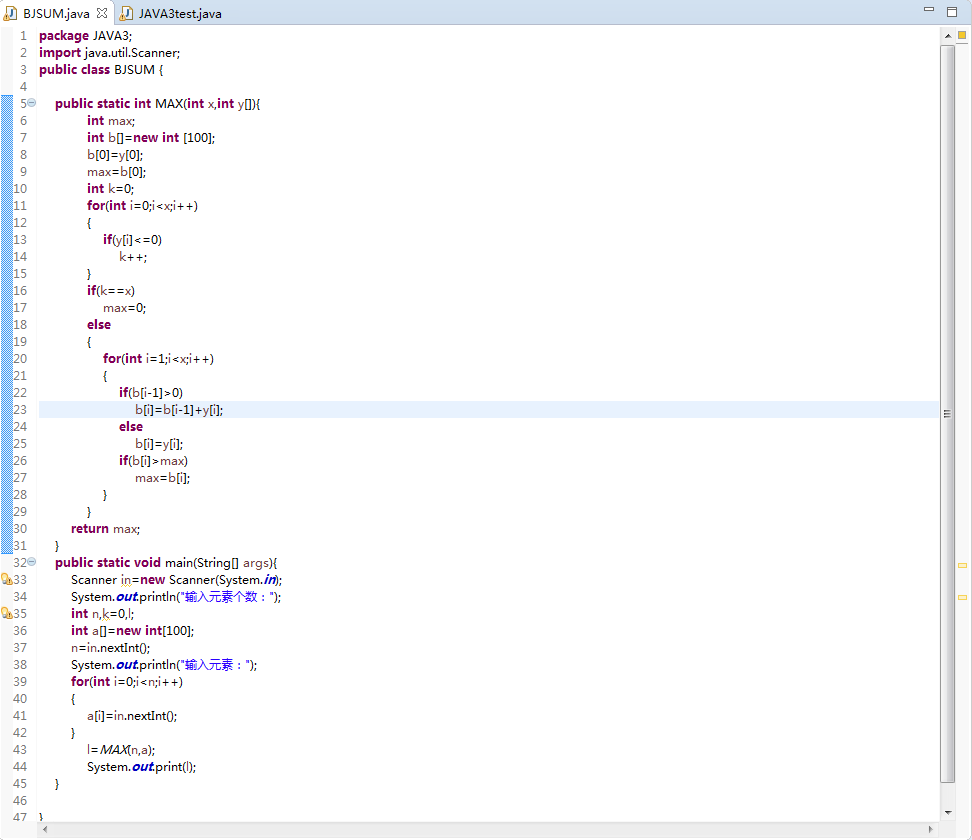
2.1运行结果如下：

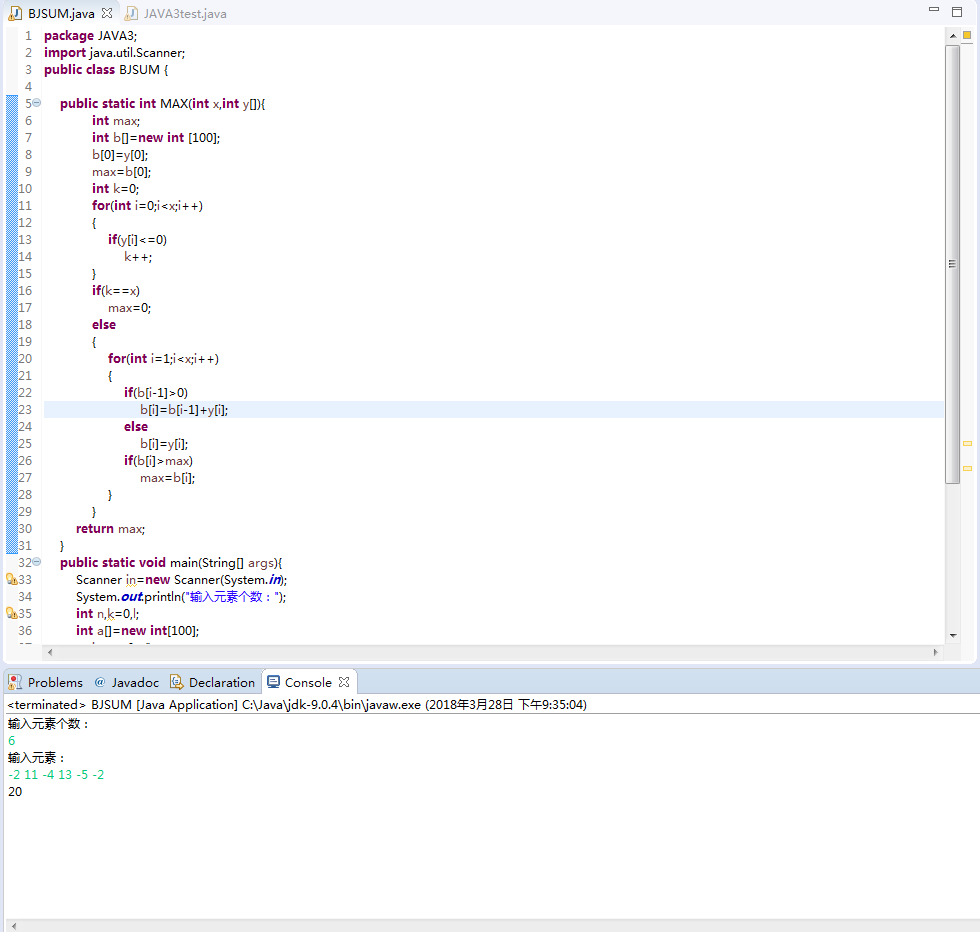
3.测试类代码如下：

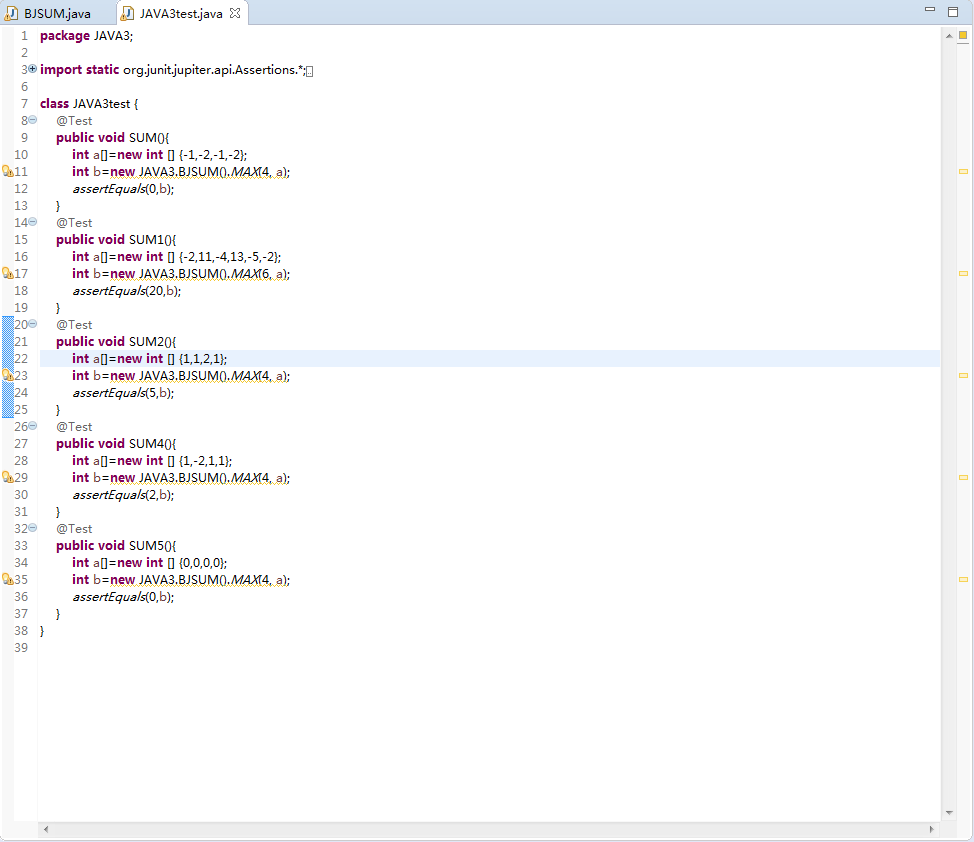
3.1测试运行结果如下：

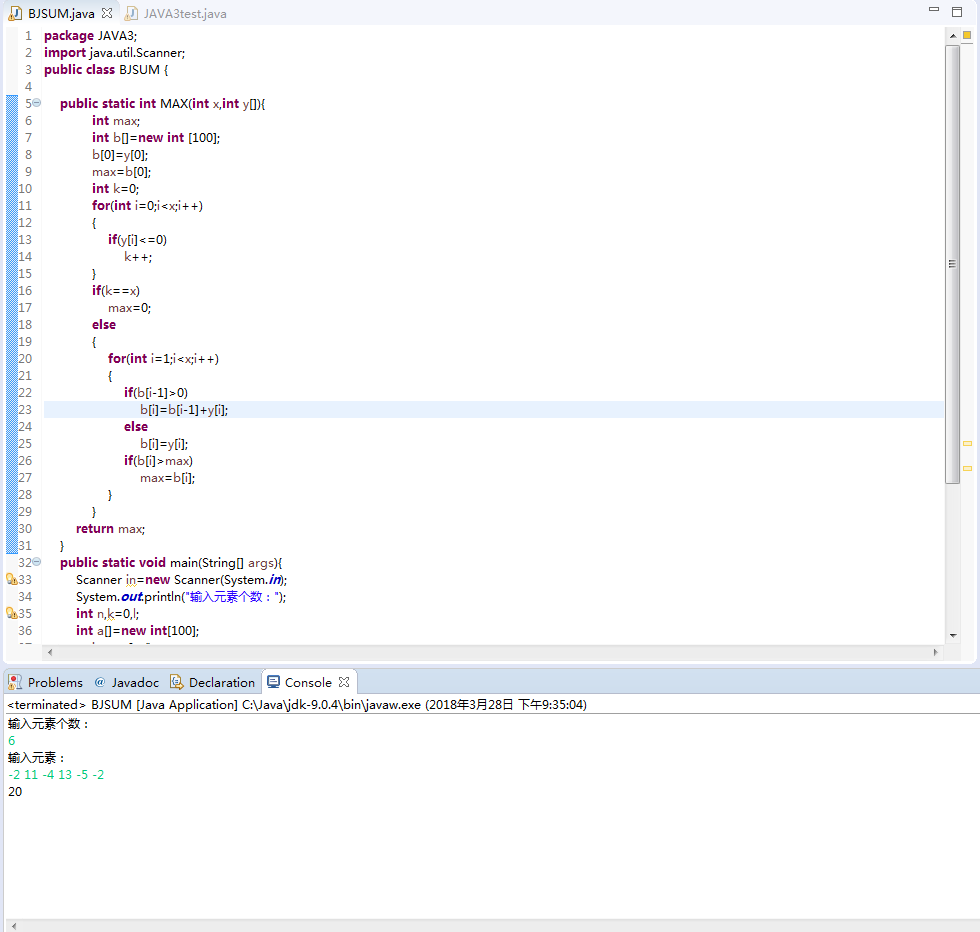
[参考算法：动态规划]（https://blog.csdn.net/HFUTLXM/article/details/78959012）
[参考测试：条件组合覆盖]（https://blog.csdn.net/skyxmstar/article/details/69092562）
具体覆盖的对不对，有点蒙········第一次尝试下回或许就会更好！现在觉得算法真的很重要也很简单！！
[代码托管]（https://coding.net/u/lmmortal/p/sum/git/blob/master/.gitignore?public=true）