数据结构课程设计——表达式求值

表达式求值

本站提供的所有内容仅供学习、交流和分享用途。如有雷同，纯属巧合。

---

一、问题分析

  1.问题描述

    任何一个表达式都是由操作数(operand)运算符(operator)和界限符(delimiter)组成的，其中，操作数可以是常量，也可以是变量；运算符可以是算术运算符、关系运算符和逻辑运算符：界限符是左右括号和标志结束的结束符。该题仅讨论简单算术表达式的求值问题，约定表达式中只包含加、减、乘、除4种运算，所有的运算对象均为简单变量，表达式的结束符为“要求以字符序列的形式从终端输入语法正确，不含变量的整数表达式”。利用已知的算符优先关系，实现对算术表达式的求值。

  2.需求分析

    （1）这是一个利用栈结构完成的程序。为了实现算符的优先算法，我们使用两个工作栈，一个称为操作符栈(OPTR),用以寄存运算符；另一个称为操作数栈(OPND)，用以寄存操作数或运算结果；

    （2）表达式以字符串的存储方式输入；

    （3）测试样例：

• • • 输入数据：1+(20+4)/(4-1)
    • 正确结果：9

---

二、概要设计

  1.主界面设计

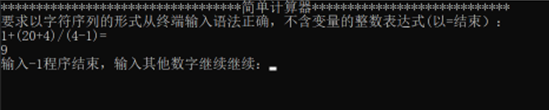
    为了实现“表达式求值系统”的功能，需要提示用户输入表达式，并提示以“=”结尾，方便用户使用。并在输入表达式后给出正确提示，若正确则输出结果，若错误则输出错误提示。输出结束后给出下一步操作的提示，若结束程序输入-1，若继续程序输入其他数字。

  2.数据结构设计

    本系统采用栈存储表达式，其中：一个工作栈称为操作符栈(OPTR)，寄存运算符；另一个工作栈称为操作数栈(OPND)，寄存操作数或运算结果。其中，base为栈底指针，top为栈顶指针，stacksize为栈最大容量。

  3.功能设计

    根据需求分析，需要设计表达式输入区，进行表达式求值的计算，并能判断表达式正确与否给出正确的提示信息或正确的结果，并提示选择继续计算或退出。求表达式主要的问题有：1.表达式是否合理；2.符号的优先级关系；3.多位数处理；4.正确求职。

  4.模块设计

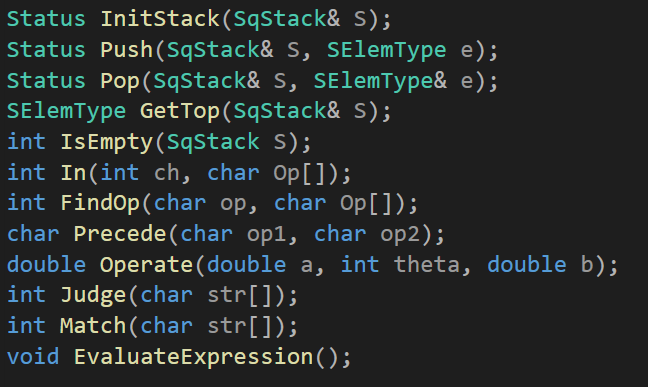
    根据功能设计，设置了 13 个函数，各函数功能及函数头设计如下：

    

---

三、详细设计

  1.数据结构定义

    （1）顺序栈

      

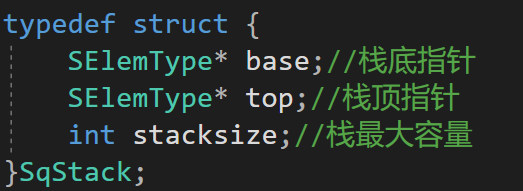
    （2）全局变量

      

---

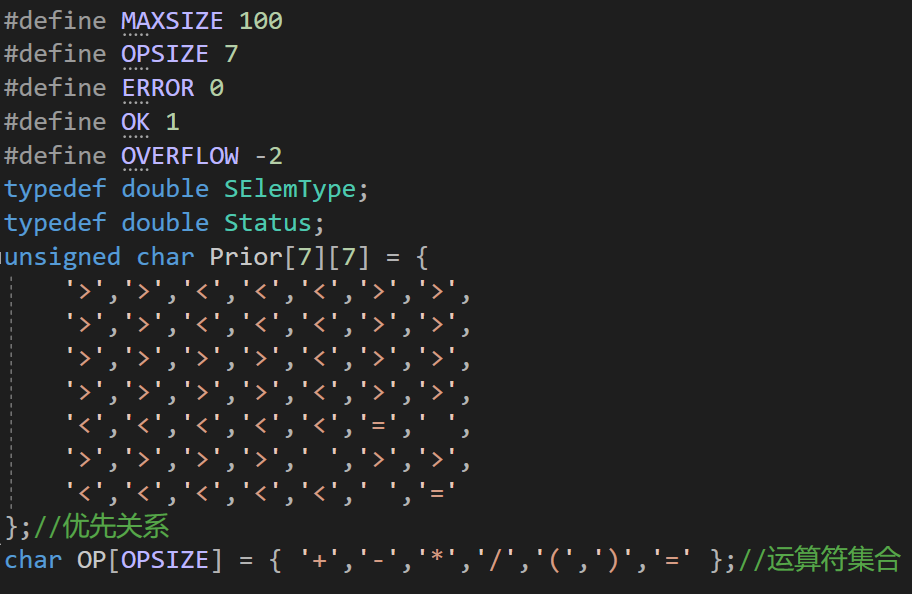
  2.主要函数设计

• • 符号的优先级关系

      算数四则运算遵循以下三条规则：

        1.先乘除后加减；

        2.从左往右运算；

        3.先括号内，后括号外；

      根据以上规则，在运算每一步中，任意两个相继出现的运算符O1和O2之间的关系至多是下面三种：

                   O1<O2;   O1的优先权低

                   O1=O2;   两优先权相等

                   O1>O2;   O1的优先权高

      则有表格：

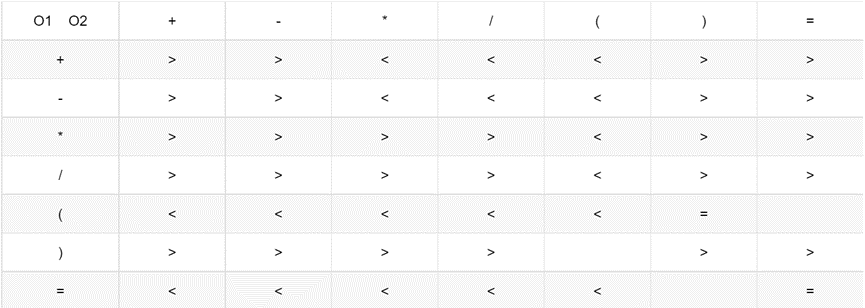
     (1)(2)(3)函数为判断符号优先级的函数

---

• • int In(int ch, char Op[])//判断读入字符ch是否为运算符

      思路：该函数判断字符ch是否为运算符，运算符在集合Op[]中定义，用for循环遍历数组，当字符ch为Op[]集合中运算符时，返回OK，反之返回ERROR；

      输入：待判断字符ch和运算符集合Op[];

      输出：该函数为int型，ch为运算符返回1，反之返回0。

• • int FindOp(char op, char Op[])//字符在优先关系表中的位置

      思路：该函数判断字符op在优先关系表中的位置，用for循环遍历优先关系表，当查找到字符ch的位置时，将此时优先关系表Op[]的数组下标的值赋给x，返回x的值；

      输入：待判断字符ch和优先关系表Op[];

      输出：该函数为int型，返回值为x的值。

• • char Precede(char op1, char op2)//判断运算符栈的栈顶元素与读入运算符之间的优先级关系的函数

      思路：FindOp()函数的值即为数组下标，通过两个下标确定栈顶元素与读入运算符的关系在二维数组Prior中的坐标，返回二者的优先关系；

      输入：带判断优先关系的两个字符op1和op2；

      输出：该函数为char型，返回op1与op2的优先关系，即‘<’‘>’‘=’

• • double Operate(double a, int theta, double b)//进行二元运算函数

      思路：通过运算符theta判断进行什么运算；

      输入：两个运算数a,b和运算符theta；

      输出：该函数为double型，返回ab运算结果，若运算符theta不为加减乘除则返回ERROR。

---

• • 判断表达式是否合理：

      1.若出现其他符号如‘？’，‘、’，‘&’等等都是错误符号，扫描时会给出相应的错误信息提示；

      2.若出现表达式输入错误，如：

        1++2++3=

        1（2+3）=

       也会给出相应的错误提示。

      3.出现括号不匹配现象如：

        （）1+2）=3

        也会给出相应的提示。

     (5)(6)函数为判断表达式子正确性的函数

---

• • int Judge(char str[])//判断表达式是否合理

      思路：输入字符串时候，需要判断该字符串的正确性，表达式第一个值和倒数第二个值不能为运算符；当遇到左括号时后一位不能为运算符，前一位不能为数字；当遇到右括号时前一位不能为运算符，后一位不能为数字，且不能在第一位；当遇到加减乘除后一位也不能为加减乘除；当遇到除号时分母不能为0；

      输入：字符数组ch[]；

      输出：该函数为int型函数，若表达式不合理，根据判断情况返回0；若表达式合理则返回1；当分母为0时给出提示“分布不能为0”；

      算法步骤：

1. 1. 1. 先判断str[0]，表达式第一个字符不能为运算符，若为运算符则返回0；
      2. 判断str[len-2]，表达式倒数第二个字符也不能为运算符，若为运算符则返回0
      3. 扫描表达式，遇到不同符号判断不同情况：
         1. 遇到左括号(时，判断不同情况：
            1. 前一位不能为数字，如：9(1+2)=，若是则返回0；
            2. 后一位不能为运算符，如：9(+8)=，若是则返回0；
            3. 且后一位不能为右括号，即()，若是则返回0；
         2. 遇到右括号)时，判断不同情况：
            1. 前一位不能为运算符，如：7*(1+)=，若是则返回0；
            2. 后一位不能为数字，如：(1+2)8=，若是则返回0；
            3. 且右括号不能在第一位，若str[i]=='('则返回0；
         3. 遇到加减乘除运算符时，后一位不能也为加减乘除，若是则返回0；
         4. 遇到除号时，根据分母不能为零原则，后一位不能为0，若为0则返回0

---

• • int Match(char str[])//判断括号是否匹配

      思路：通过用过两个标记，遇到左括号将-1入栈，遇到右括号了就将-1出栈，当遇到“)”时，栈中没有元素则Pop(S,y)=0，匹配失败；遍历完数组之后，若栈非空则匹配失败；

      输入：字符数组ch[]；

      输出：该函数为int型，若括号匹配返回1，若不匹配则返回0。

      算法步骤：

1. 1. 1. 先初始化栈S，设置标记x,y，用strlen()获取字符串长度
      2. 扫描表达式，判断不同情况：
         1. 若ch为‘(’，将-1入栈
         2. 若ch为‘)’，将标记出栈，判断是否出栈成功，若不成功则匹配失败，返回0；
      3. 最后判断栈是否为空
         
         1. 若为空，则说明括号匹配成功，返回1；
         2. 若不为空，则匹配不成功，返回0；

---

• • void EvaluateExpression()//表达式求值

      输入：表达式ch；

      输出：若输入正确，返回栈顶元素的值，即表达式的运算结果；若输入错误则提示错误信息；

      算法步骤：

1. 1. 1. 初始化OPTR栈和OPND栈，将表达式起始符“=”压入OPTR栈
      2. 扫描表达式，读入第一个字符ch，如果表达式没有扫描完毕至“=”或OPTR的栈顶元素不为“=”时，则执行以下操作：
         1. 若ch不是操作符，则压入OPND栈，读入下一字符ch；
         2. 若ch是运算符，则根据OPTR的栈顶元素和ch的优先级比较结果，做不同的处理：
            1. 若是小于，则ch压入OPTR栈，读入下一字符ch；
            2. 若是大于，则弹出OPTR的栈顶运算符，从OPND栈弹出两个数，进行相应运算，结果压入OPND栈；
            3. 若是等于，则OPTR的栈顶元素是‘(’且ch是‘)’，这时弹出OPTR栈顶的‘(’，相当于括号匹配成功，读入下一字符
      3. OPND栈顶元素即为表达式求值结果，返回此元素

---

• • 多位数处理：

      当扫描ch为操作数时，ch只能一个一个入栈，则出现多位数时，会拆分变成一个一个入栈，为了解决这个方法，可以利用flag判断标记和q保存。输入一个操作数时，先将其保存在q，并令q*10+ch；flag=1；再输入下一个字符ch，知道ch为符号数时，将q的值入OPND栈，最后把q=0和flag=0还原再读入下一个字符ch。

---

四、测试

  1.表达式合法情况：

    

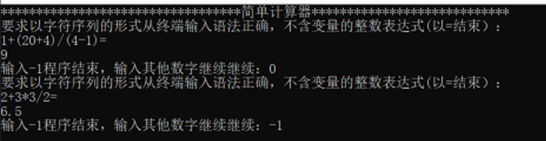
  2.表达式不合法情况

    

---

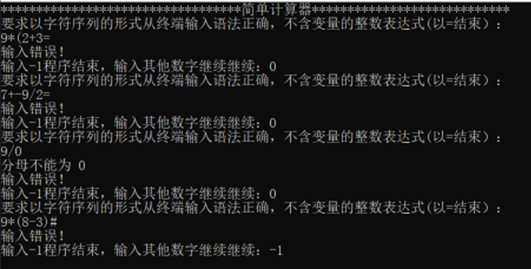
五、代码清单（带注释）

#include<stdio.h>
#include <conio.h>
#include<string.h>
#include <stdlib.h>
#include <iostream>
using namespace std;

#define MAXSIZE 100
#define OPSIZE 7
#define ERROR 0
#define OK 1
#define OVERFLOW -2

typedef double SElemType;
typedef double Status;

unsigned char Prior[7][7] = {
	'>','>','<','<','<','>','>',
	'>','>','<','<','<','>','>',
	'>','>','>','>','<','>','>',
	'>','>','>','>','<','>','>',
	'<','<','<','<','<','=',' ',
	'>','>','>','>',' ','>','>',
	'<','<','<','<','<',' ','='
};//优先关系
char OP[OPSIZE] = { '+','-','*','/','(',')','=' };//运算符集合

typedef struct {
	SElemType* base;//栈底指针
	SElemType* top;//栈顶指针
	int stacksize;//栈最大容量
}SqStack;

Status InitStack(SqStack& S) {//初始化
	S.base = new SElemType[MAXSIZE];//分配最大容量为MAXSIZE的数组空间
	if (!S.base)
		exit(OVERFLOW);//存储空间分配失败
	S.top = S.base;
	S.stacksize = MAXSIZE;
	return OK;
}
Status Push(SqStack& S, SElemType e) {//入栈
	if (S.top - S.base == S.stacksize)
		return ERROR;//栈满
	*(S.top)++ = e;//元素e压入栈顶，栈顶指针加一
	return OK;
}
Status Pop(SqStack& S, SElemType& e) {//出栈
	if (S.top == S.base)
		return ERROR;//栈空
	e = *--S.top;//栈顶指针减一，将栈顶元素赋给e
	return OK;
}
SElemType GetTop(SqStack& S) {//返回S的栈顶元素
	if (S.top != S.base)//栈非空
		return *(S.top - 1);
}
int IsEmpty(SqStack S) {//判空
	if (S.top == S.base)
		return OK;
	return ERROR;
}

int In(int ch, char Op[]) {//判断读入字符ch是否为运算符
	for (int i = 0; i < OPSIZE; i++) {
		if (ch == Op[i])
			return OK;
	}
	return ERROR;
}
int FindOp(char op, char Op[]) {//字符在优先关系表中的位置
	int x;
	for (int i = 0; i < OPSIZE; i++)
		if (op == Op[i])
			x = i;
	return x;
}
char Precede(char op1, char op2) {//判断运算符栈的栈顶元素与读入运算符之间的优先级关系的函数
	return Prior[FindOp(op1, OP)][FindOp(op2, OP)];
}
double Operate(double a, int theta, double b)
{//进行二元运算函数
	switch (theta)
	{
	case '+':
		return a + b;
		break;
	case '-':
		return a - b;
		break;
	case '*':
		return a * b;
		break;
	case'/':
		return a / b;
		break;
	default:
		return ERROR;
	}
}
int Judge(char str[])
{//判断表达式是否合理
	int len = strlen(str);
	if (str[0] == '/' || str[0] == '*')
		return 0;
	if (str[len - 1] < '0' && str[len - 1]>'9')
		return 0;
	for (int i = 0; i < len; i++)
	{
		if (str[i] == '(')
		{
			if (i == 0 && (str[i + 1] == '*' || str[i + 1] == '/') || str[i + 1] == '=')
				return 0;
			if (str[i + 1] == ')')
				return 0;
			if (str[i - 1] >= '0' && str[i - 1] <= '9')
				return 0;
		}
		if (str[i] == ')')
		{
			if (i == 0)
				return 0;
			if (str[i - 1] == '+' || str[i - 1] == '*' || str[i - 1] == '-' || str[i - 1] == '/')
				return 0;
			if (str[i + 1] >= '0' && str[i + 1] <= '9')
				return 0;
			if (str[i + 1] >= '0' && str[i + 1] <= '9' && i < len - 1)
				return 0;
		}
		if ((str[i] == '+' || str[i] == '-' || str[i] == '*' || str[i] == '/'))
		{
			if (str[i + 1] == '+' || str[i + 1] == '-' || str[i + 1] == '*' || str[i + 1] == '/')
				return 0;
		}
		if (str[i] == '/') 
		{
			if (str[i + 1] == '0') 
			{
				cout << "分母不能为 0" << endl;
				return 0;
			}
		}
	}
	return 1;
}
int Match(char str[])
{//判断括号是否匹配
	SqStack S;
	InitStack(S);//初始化
	double y;//标记1
	double x = -1;//标记2
	int len = strlen(str);//获取长度
	for (int i = 0; i < len; i++)//用for循环遍历
	{
		char ch = str[i];
		switch (ch)
		{
		case '('://若是左括号
			Push(S, x);//标记-1入栈
			break;
		case ')'://若为右括号
			if (Pop(S, y) == 0)//若没有出栈，则不匹配Pop返回值为0
				return 0;
			break;
		}
	}
	int k = IsEmpty(S);
	if (k == 1)//判断栈空
		return 1;
	else
		return 0;
}
void EvaluateExpression()
{//表达式求值
	SqStack OPND;//操作数栈
	SqStack OPTR;//操作符栈
	InitStack(OPND);
	InitStack(OPTR);
	double theta, a, b, x;
	char ch[MAXSIZE];//定义数组 保存算术表达式
	Push(OPTR, '=');//开始时将'='进OPTR栈
	cin >> ch;

	char ch2;
	ch2 = ch[0];
	double t = 0;//记录多值；
	int flag = 1;// 判断多值数是否入栈；
	int i = 0, len;//len为字符串长度
	len = strlen(ch);

	int k1 = Judge(ch);//判断表达式是否合理
	int k2 = Match(ch);//判断括号是否匹配
	if (k2 == 0)
	{
		cout << "输入错误！" << endl;
		return;
	}
	if (k2 == 1)
	{
		if (k1 == 0)
			cout << "输入错误！" << endl;
		else
		{
			while (ch2 != '=' || GetTop(OPTR) != '=')//表达式没有扫描完或OPTR栈顶元素不为=
			{
				if (ch2 >= '0' && ch2 <= '9')
				{
					ch2 -= '0';
					t = t * 10 + ch2;//多位数保存
					if (len < 3 && ch[len - 1] == '=')
					{
						cout << t << endl;
						return;
					}
					flag = 1;//判断多位数是否入栈
					i++;
					ch2 = ch[i];//提取下一个字符
				}
				else if (In(ch2, OP))//若ch2为运算符
				{
					if (flag == 1)//若flag=1，则将多位数入栈
					{
						Push(OPND, t);
						t = 0;
						flag = 0;
					}
					switch (Precede(GetTop(OPTR), ch2))//比较OPTR栈顶元素和ch2的优先级
					{
					case '<'://当前字符ch2压入OPTR栈，读入下一字符ch
						Push(OPTR, ch2);
						i++;
						ch2 = ch[i];
						break;
					case '>':
						Pop(OPTR, theta);//弹出运算符
						Pop(OPND, b);//弹出位于栈顶的两个运算数
						Pop(OPND, a);
						Push(OPND, Operate(a, theta, b));//将运算结果压入OPND栈
						break;
					case '='://OPTR栈顶元素为(且ch1为)
						Pop(OPTR, x);//弹出(
						i++;
						ch2 = ch[i];//读入下一个字符ch
						break;
					}

				}
				else
				{
					cout << "输入错误！" << endl;
					getchar();
					return;
				}
			}
			cout << GetTop(OPND) << endl;
		}
	}	
}
int main()
{
	cout << "**********************************简单计算器****************************" << endl;
	int n = 0;
	for (int i = 0;; i++)
	{
		if (n == -1)
			break;
		cout << "要求以字符序列的形式从终端输入语法正确，不含变量的整数表达式(以=结束）：" << endl;
		EvaluateExpression();
		cout << "输入-1程序结束，输入其他数字继续继续：";
		cin >> n;
	}
}