二叉树的建立方法总结

之前已经介绍了二叉树的四种遍历(如果不熟悉请戳我)，下面介绍一些二叉树的建立方式。首先需要明确的是，由于二叉树的定义是递归的，所以用递归的思想建立二叉树是很自然的想法。

1. 交互式问答方式

这种方式是最直接的方式，就是先询问用户根节点是谁，然后每次都询问用户某个节点的左孩子是谁，右孩子是谁。代码如下(其中字符'#'代表空节点)：

#include <cstdio>
#include <cstdlib>

using namespace std;

typedef struct BTNode *Position;
typedef Position BTree;
struct BTNode
{
    char data;
    Position lChild, rChild;
};

BTree CreateBTree(BTree bt, bool isRoot)
{
    char ch;
    if (isRoot)
        printf("Root: ");
    fflush(stdin);         /* 清空缓存区 */
    scanf("%c", &ch);
    fflush(stdin);
    if (ch != '#')
    {
        isRoot = false;
        bt = new BTNode;
        bt->data = ch;  
        bt->lChild = NULL;
        bt->rChild = NULL;
        printf("%c's left child is: ", bt->data);
        bt->lChild = CreateBTree(bt->lChild, isRoot);
        printf("%c's right child is: ", bt->data);
        bt->rChild = CreateBTree(bt->rChild, isRoot);
    }
    return bt;
}

int main()
{
    BTree bt;
    bt = CreateBTree(bt, true);
    LevelOrderTraversal(bt);        /* 层序遍历 */

    return 0;
}

2. 根据先序序列

例如输入序列ABDH##I##E##CF#J##G##（#表示空），则会建立如下图所示的二叉树

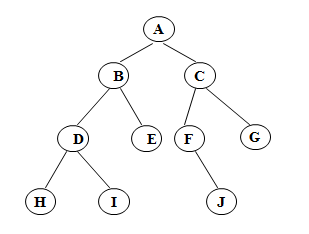
思路和第一种方式很相似，只是代码实现细节有一点区别，这里给出创建函数

BTree CreateBTree()
{
    BTree bt = NULL;
    char ch;
    scanf("%c", &ch);
    if (ch != '#')
    {
        bt = new BTNode;
        bt->data = ch;
        bt->lChild = CreateBTree();
        bt->rChild = CreateBTree();
    }
    return bt;
}

3. 根据中序序列和后序序列

和方式二不同的是，这里的序列不会给出空节点的表示，所以如果只给出先序序列，中序序列，后序序列中的一种，不能唯一确定一棵二叉树。但是如果给出中序序列和后序序列或者先序序列和中序序列就可以唯一确定一棵树。根据三种遍历方式的特点，我们可以利用先序序列或后序序列确定根节点，可以利用中序序列确定左右孩子。

由后序序列“左子树->右子树->根节点”性质可知后序序列的最后一个一定为这棵树的根节点，而又根据中序序列“左子树->根节点->右子树”的性质，由后序序列得到的根节点可以将中序序列分为左子树中序序列和右子树中序序列。然后根据序列的个数相同，可以将后序序列分为左子树后序序列和右子树后序序列。依次递归的进行，直到序列长度为空递归返回。同理，根据先序序列的“根节点->左子树->右子树”性质可得先序序列的第一个一定为这棵树的根节点，之后与上述类似。

例如：一棵二叉树的中序序列为：ABCEFGHD，后序序列为: ABFHGEDC。建立的二叉树如下图：

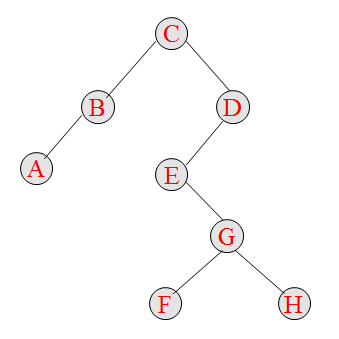
代码如下：

/*
通过中序序列和后序序列建树，然后先序遍历输出
输入（第一行为中序，第二行为后序）：
ABCEFGHD
ABFHGEDC
输出：
CBADEGFH

*/
#include <cstdio>
#include <cstdlib>

using namespace std;

const int N = 1010;

typedef struct BTNode *Position;
typedef Position BTree;
struct BTNode
{
    char data;
    Position lChild, rChild;
};

BTree CreateBTree(char inOd[], char postOd[], int n);
void PreOrder(BTree bt);

int main()
{
    char inOd[N], postOd[N];  /* 中序序列与后序序列 */
    int n = 0;
    char ch;
    while ((ch = getchar()) && ch != '\n')
        inOd[n++] = ch;
    n = 0;
    while ((ch = getchar()) && ch != '\n')
        postOd[n++] = ch;

    BTree bt = CreateBTree(inOd, postOd, n);
    PreOrder(bt);
    printf("\n");

    return 0;
}

BTree CreateBTree(char inOd[], char postOd[], int n)
{
    if (n == 0)
        return NULL;

    BTree btRoot = new BTNode;
    btRoot->data = postOd[n-1];     //后序序列最后一个元素一定是根节点
    char lInOd[N], rInOd[N];
    char lPostOd[N], rPostOd[N];
    int n1, n2;
    n1 = n2 = 0;
    //根据根节点将中序序列分为左子树和右子树
    for (int i = 0; i < n; i++)
    {
        if (i <= n1 && inOd[i] != btRoot->data)
            lInOd[n1++] = inOd[i];
        else if (inOd[i] != postOd[n-1])
            rInOd[n2++] = inOd[i];
    }
    //根据一个树的后序序列的长度等于中序序列且后序遍历是先左子树再右子树
    //将后序序列分为左子树和右子树
    int m1, m2;
    m1 = m2 = 0;
    for (int i = 0; i < n-1; i++)
    {
        if (i < n1)
            lPostOd[m1++] = postOd[i];
        else
            rPostOd[m2++] = postOd[i];
    }
    btRoot->lChild = CreateBTree(lInOd, lPostOd, n1);
    btRoot->rChild = CreateBTree(rInOd, rPostOd, n2);
    return btRoot;
}

void PreOrder(BTree bt)
{
    if (bt != NULL)
    {
        printf("%c", bt->data);
        PreOrder(bt->lChild);
        PreOrder(bt->rChild);
    }
}

4. 根据不完整的先序，中序，后序序列

如果同时给出先序，中序，后序三种序列，但都是不完整的，能否建立一课二叉树呢？考虑下面一个例子：

     一棵二叉树的先序、中序和后序序列分别如下，其中一部分未显示出来，试编程求出空格处的内容。

      先序：_B_F_ICEH_G

      中序：D_KFIA_EJC_

      后序：_K_FBHJ_G_A

事实上，上述例子的核心思想还是方式三中先找到根节点，再分为左右子树，然后递归进行。区别是这里不能唯一的根据先序或后序来确定根节点，故需要判断当前是先序序列还是后序序列可以得到根节点，所以函数实现需要传递先序中序后序3种序列。而此题还有一个隐含的条件，就是当先序和后序都不能得到根节点时，中序序列存在且只存在一个'_'，而且'_'就是根节点所在位置。这样分析之后代码就比较好实现了。代码如下：

/*
一棵二叉树的先序、中序和后序序列分别如下，其中一部分未显示出来，
试根据三个不完整的序列建树，然后依次输出先，中，后序的完整序列。
输入：
_B_F_ICEH_G
D_KFIA_EJC_
_K_FBHJ_G_A
输出：
ABDFKICEHJG
DBKFIAHEJCG
DKIFBHJEGCA

*/

#include <cstdio>
#include <cstdlib>

using namespace std;

const int N = 1010;

typedef struct BTNode *Position;
typedef Position BTree;
struct BTNode
{
    char data;
    Position lChild, rChild;
};

BTree CreateBTree(char preOd[], char inOd[], char postOd[], int n);
void PreOrder(BTree bt);
void InOrder(BTree bt);
void PostOrder(BTree bt);

int main()
{
    char preOd[N], inOd[N], postOd[N];
    int n = 0;
    char ch;
    while ((ch = getchar()) && ch != '\n')
        preOd[n++] = ch;
    n = 0;
    while ((ch = getchar()) && ch != '\n')
        inOd[n++] = ch;
    n = 0;
    while ((ch = getchar()) && ch != '\n')
        postOd[n++] = ch;

    BTree bt = CreateBTree(preOd, inOd, postOd, n);
    PreOrder(bt);
    printf("\n");
    InOrder(bt);
    printf("\n");
    PostOrder(bt);
    printf("\n");

    return 0;
}

BTree CreateBTree(char preOd[], char inOd[], char postOd[], int n)
{
    if (n == 0)
        return NULL;
    BTree btRoot = new BTNode;
    if (n == 1)
    {
        if (preOd[0] != '_')
            btRoot->data = preOd[0];
        else if (inOd[0] != '_')
            btRoot->data = inOd[0];
        else if (postOd[0] != '_')
            btRoot->data = postOd[0];
        else
        {
            printf("Input error!\n");
            exit(0);
        }
        btRoot->lChild = NULL;
        btRoot->rChild = NULL;
        return btRoot;
    }
    if (postOd[n-1] != '_')
        btRoot->data = postOd[n-1];     //后序序列最后一个元素一定是根节点
    else if (preOd[0] != '_')
        btRoot->data = preOd[0];
    else
    {
        printf("Input Error!\n");
        exit(0);
    }
    char lPreOd[N], rPreOd[N];
    char lInOd[N], rInOd[N];
    char lPostOd[N], rPostOd[N];
    int n1, n2;
    n1 = n2 = 0;
    //根据根节点将中序序列分为左子树和右子树
    int flag = 0;   //判断根节点是否在中序序列中
    for (int i = 0; i < n; i++)
    {
        if (inOd[i] == btRoot->data)
        {
            flag = 1;
            break;
        }
    }
    if (flag == 1)  //如果根节点存在，按根节点划分
    {
        for (int i = 0; i < n; i++)
        {
            if (i <= n1 && inOd[i] != btRoot->data)
                lInOd[n1++] = inOd[i];
            else if (inOd[i] != btRoot->data)
                rInOd[n2++] = inOd[i];
        }
    }
    else        //如果根节点不存在，按'_'划分
    {
        for (int i = 0; i < n; i++)
        {
            if (i <= n1 && inOd[i] != '_')
                lInOd[n1++] = inOd[i];
            else if (inOd[i] != '_')
                rInOd[n2++] = inOd[i];
        }
    }

    //根据一个树的后序序列的长度等于中序序列且后序遍历是先左子树再右子树
    //将后序序列分为左子树和右子树
    int m1, m2;
    m1 = m2 = 0;
    for (int i = 0; i < n-1; i++)
    {
        if (i < n1)
            lPostOd[m1++] = postOd[i];
        else
            rPostOd[m2++] = postOd[i];
    }
    //根据一个树的先序序列的长度等于中序序列且先序遍历是除根节点外也是先左子树再右子树
    //将先序序列分为左子树和右子树
    m1 = m2 = 0;
    for (int i = 1; i < n; i++)
    {
        if (i < n1 + 1)
            lPreOd[m1++] = preOd[i];
        else
            rPreOd[m2++] = preOd[i];
    }
    btRoot->lChild = CreateBTree(lPreOd, lInOd, lPostOd, n1);
    btRoot->rChild = CreateBTree(rPreOd, rInOd, rPostOd, n2);

    return btRoot;
}

void PreOrder(BTree bt)
{
    if (bt != NULL)
    {
        printf("%c", bt->data);
        PreOrder(bt->lChild);
        PreOrder(bt->rChild);
    }
}

void InOrder(BTree bt)
{
    if (bt != NULL)
    {
        InOrder(bt->lChild);
        printf("%c", bt->data);
        InOrder(bt->rChild);
    }
}

void PostOrder(BTree bt)
{
    if (bt != NULL)
    {
        PostOrder(bt->lChild);
        PostOrder(bt->rChild);
        printf("%c", bt->data);
    }
}