Pell方程

Pell方程

一.定义

Pell方程是指形如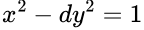的二元二次不定方程，其中d是一个非完全平方的正整数，x和y为要求解的整数。

当d为完全平方数时，比如d= k^2,方程

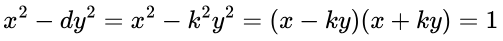
而当d不是完全平方数时，Pell方程有无限多组整数解

在所有解中，存在x1,y1使得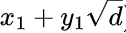最小，则称（x1,y1）是方程的基本解

二.基本解的求解方法

1.连分数法

在此之前，先介绍一下连分数和渐进分数，之前在wiener攻击提到过，但是学得比较浅，这里再认真领悟一下

连分数：

连分数是指将一个数表示为如下形式：

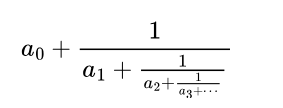
其中a0可以为任意实数（通常为整数），而a1,a2,a3...是正实数（通常为整数）。简记为：[a0;a1,a2,a3,...]

根据连分数项数是否有限分为有限连分数和无限连分数

其中无限连分数具有以下特点：（后面解Pell方程会涉及到）

• 良好的逼近性：无限连分数通过截断得到一系列的渐进分数
  
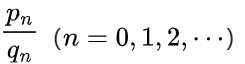
  。这些渐进分数逐渐逼近原无线连分数所表示的数，在分母不超过qn的所有有理数中，第n个渐进分数
  
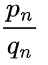
  最接近原无线连分数
• 周期性：从a1开始，并且周期的最后一个数是a0的2倍
• 唯一性：无理数和无限连分数之间一一对应

连分数的计算方法：

有理数转换成连分数：

无理数转换成连分数：

渐进分数：

对于一个连分数 [a0;a1,a2,a3,...,an]（有限连分数）或 [a0;a1,a2,a3,...]（无限连分数),它的渐进分数是指通过逐步截断连分数得到的一系列有限连分数所表示的有理数，越往后结果越接近真实值

这里放一个例子，有助于理解

另外，可以通过递推公式计算连分数的渐进分数：

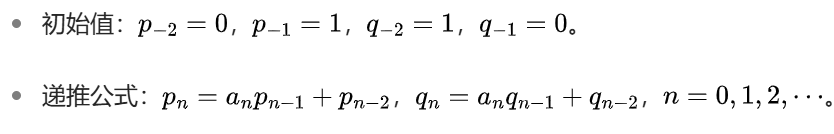
连分数法求解Pell方程：

核心思想是利用二次无理数

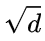
的连分数展开及其渐进分数的性质来找到方程的基本解

sagemath实现：

def Pell(D,numbers=100):
	temp = continued_fraction(sqrt(D))
	for i in range(number):
		denom = temp.denominator(i) # 分母
		num = temp.numerator(i) # 分子
		if num^2 - D*denom^2 == 1:
			return num,denom
	return None,None
Pell(D)

python实现：

import math

def continued_fraction_sqrt(d):
    # 初始化变量
    m = 0
    d_ = 1
    a0 = int(math.sqrt(d))
    a = a0
    p0, p1 = 1, a0
    q0, q1 = 0, 1

    while True:
        # 计算连分数的下一项
        m = d_ * a - m
        d_ = (d - m ** 2) // d_
        a = (a0 + m) // d_

        # 计算渐近分数的分子和分母
        p2 = a * p1 + p0
        q2 = a * q1 + q0

        # 检查是否为 Pell 方程的解
        if p2 ** 2 - d * q2 ** 2 == 1:
            return p2, q2

        # 更新变量
        p0, p1 = p1, p2
        q0, q1 = q1, q2

# 示例：求解 x^2 - 2y^2 = 1 的最小解
d = 2
x, y = continued_fraction_sqrt(d)
print(f"Pell 方程 x^2 - {d}y^2 = 1 的最小解为 (x={x}, y={y})")

python的实现没太看明白。。。

下面这张图有一点点帮助

2.爆破

基本思路是从 (y = 1) 开始逐个尝试，计算对应的

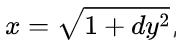
，检查 x 是否为整数，如果是，则 (x,y)就是 Pell 方程的基本解

python实现：

import math

def brute_force_pell(d):
    # 检查 d 是否为完全平方数，如果是则抛出异常
    if int(math.sqrt(d))**2 == d:
        raise ValueError("d 不能是完全平方数")
    y = 1
    while True:
        # 计算 x 的平方
        x_squared = 1 + d * y**2
        # 计算 x
        x = math.sqrt(x_squared)
        # 检查 x 是否为整数
        if x.is_integer():
            return int(x), y
        # 如果不是整数，y 加 1 继续尝试
        y += 1

# 示例：求解 x^2 - 2y^2 = 1 的基本解
d = 2
try:
    x, y = brute_force_pell(d)
    print(f"Pell方程 x^2 - {d}y^2 = 1 的基本解为 (x={x}, y={y})")
except ValueError as e:
    print(e)

三.求任意解

迭代法：

迭代公式：

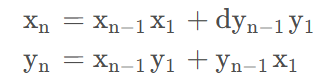
python实现：

def get_pell_solutions(d, x1, y1, num_solutions):
    solutions = [(x1, y1)]
    x_n, y_n = x1, y1
    for _ in range(num_solutions - 1):
        x_next = x1 * x_n + d * y1 * y_n
        y_next = x1 * y_n + y1 * x_n
        solutions.append((x_next, y_next))
        x_n, y_n = x_next, y_next
    return solutions

# 示例：对于 Pell 方程 x^2 - 2y^2 = 1，已知基本解 (x1, y1) = (3, 2)
d = 2
x1, y1 = 3, 2
num_solutions = 5  # 求前 5 组解

solutions = get_pell_solutions(d, x1, y1, num_solutions)
for i, (x, y) in enumerate(solutions, start=1):
    print(f"第 {i} 组解: (x={x}, y={y})")

由于直接迭代的时间复杂度为O（n）,如果n过大，计算时间会很长，所以我们可以用矩阵快速幂的方法，时间复杂度为log n

矩阵快速幂法:

迭代公式可以表示成如下形式：

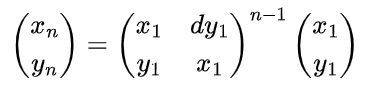
python实现：

import numpy as np

def matrix_power(matrix, n):
    """矩阵快速幂函数"""
    result = np.eye(2, dtype=int)
    while n > 0:
        if n % 2 == 1:
            result = np.dot(result, matrix)
        matrix = np.dot(matrix, matrix)
        n //= 2
    return result

def pell_solution_by_matrix(d, x1, y1, n):
    """使用矩阵快速幂求解Pell方程的第n组解"""
    matrix = np.array([[x1, d * y1], [y1, x1]], dtype=int)
    power_matrix = matrix_power(matrix, n - 1)
    vector = np.array([[x1], [y1]], dtype=int)
    solution = np.dot(power_matrix, vector)
    x_n = solution[0][0]
    y_n = solution[1][0]
    return x_n, y_n

# 示例：对于Pell方程x^2 - 2y^2 = 1，基本解 (x1, y1) = (3, 2)
d = 2
x1, y1 = 3, 2
n = 3  # 求第3组解
x_n, y_n = pell_solution_by_matrix(d, x1, y1, n)
print(f"Pell方程x^2 - {d}y^2 = 1的第 {n} 组解为 (x={x_n}, y={y_n})")

这里学习一下numpy库中的几个函数：

1.eye()

用于创建一个指定行数和列数的单位矩阵

语法：numpy.eye(N,M=None,k=0,dtype=float)

• N:必须参数，表示矩阵行数
• M：可选参数，表示矩阵的列数。如果不提供该参数，则默认列数等于行数
• k:可选参数，整数类型，用于指定主对角线的偏移量。默认值为 0，表示主对角线，k>0,向上偏移，k<0向下偏移
• dtype:可选参数，用于指定矩阵元素的数据类型，默认是 float

2.dot()

用于计算两个一维数组（向量）或多维数组（矩阵）的积