RSA常见题型三
1.小明文攻击
攻击原理:
当明文较小时,攻击者可以通过穷举m可能的值,计算m ^ e % n,并和已知的密文c相比,则可找到明文。除了穷举,还可以通过数学关系找到明文,例如,当密文c为1时,可以推测明文也为1
例题:
题目:
flag = 25166751653530941364839663846806543387720865339263370907985655775152187319464715737116599171477207047430065345882626259880756839094179627032623895330242655333
n = 134109481482703713214838023035418052567000870587160796935708584694132507394211363652420160931185332280406437290210512090663977634730864032370977407179731940068634536079284528020739988665713200815021342700369922518406968356455736393738946128013973643235228327971170711979683931964854563904980669850660628561419
题目已知密文flag和模数n,直接穷举
假设e的值小于2 ^ 10 ,又因为c = m ^ e % n ,则m ^ e =c+ i * n,假设i<10(e和i的值取得合适就行,可根据实际情况修改其取值范围)
具体解密代码如下:
import gmpy2
from Crypto.Util.number import long_to_bytes
import sympy
flag = 25166751653530941364839663846806543387720865339263370907985655775152187319464715737116599171477207047430065345882626259880756839094179627032623895330242655333
n = 134109481482703713214838023035418052567000870587160796935708584694132507394211363652420160931185332280406437290210512090663977634730864032370977407179731940068634536079284528020739988665713200815021342700369922518406968356455736393738946128013973643235228327971170711979683931964854563904980669850660628561419
e=2
while e<2 ** 10:
i=0 #注意,i从0开始
while i<10:
res=gmpy2.iroot(flag+i * n,e)
if res[1]:
m=res[0]
print(long_to_bytes(m))
i+=1
e=sympy.nextprime(e)
2.共模攻击
攻击原理:
假设存在两个用户,公钥分别为(e1,n)和(e2,n),对应的私钥分别为(d1,n)和(d2,n)
。特点:具有相同的模数n。若已知c1,c2,以及e1,e2,n,则可以通过扩展欧几里得 算法找到整数x和y,使得e1 * x + e2 * y = gcd(e1,e2)
若 gcd(e1,e2) = 1,则m = (c1 ^ x * c2 ^ (-y))% n
证明:
因为c1 =m ^ e1 mod n , c2 = m ^ e2 mod n
(c1 ^ x *c2 ^ y) mod n = ((m ^e1 mod n) ^ x * (m ^ e2 mod n) ^ y mod n) mod n
(c1 ^ x *c2 ^ y) mod n = (m ^ (e1 * x +e2 * y)) mod n
又因为e1 * x + e2 * y = gcd(e1,e2) = 1
所以(c1 ^ x *c2 ^ y) mod n = m ^1 mod n
即 c1 ^ x *c2 ^ y = m
注意:x和y中有一个为负数,假设y为负数,则应该先求c2的模反元素(即乘法逆元),再求模反元素的(-y)次幂
例题1:
题目:
from secret import e
from Crypto.Util.number import getStrongPrime, isPrime
p = getStrongPrime(1024)
q = getStrongPrime(1024)
N = p * q
phi = (p - 1) * (q - 1)
with open('flag.txt', 'rb') as f:
flag = int.from_bytes(f.read(), 'big')
assert(isPrime(e))
assert(isPrime(e + 2))
assert(isPrime(e + 4))
e1 = pow(e, 0x10001, phi)
e2 = pow(e + 2, 0x10001, phi)
e3 = pow(e + 4, 0x10001, phi)
c1 = pow(flag, e1, N)
c2 = pow(flag, e2, N)
c3 = pow(flag, e3, N)
print(f'p = {p}')
print(f'q = {q}')
print(f'c1 = {c1}')
print(f'c2 = {c2}')
print(f'c3 = {c3}')
p = 167710954518007348037383082265231465648795974011761905177264545864288011527333715495850532989338171489309608848431113452814709692343039027970312735521415071265608660628968391884287240987858607818275329135585153511665148279408708087727501421558738163577629329044315775019460018956186674179846621352371150072281
q = 130354329753344570838569091064852072757046774566775609047544069941246798511317343102715733555464772099991834579660053860799207243561908291522943696711982657846373844514551117658179060004064010647453939332217996817580433587341521331941287365948919907797478197717562721233289937471168288241937022054501586986443
c1 = 2560344169447809042170685026483682125499025654554670516499742981486615082413150123244985585751880264831112089324011804397189638172356179296987581738515619297036118472798499254785110885662931526277474101787493114656242031264678448394380651657330967744585361662315313462698221954777506355498445242300193032704972074020068699180111637362566860530694807230108024167631423062629721393506643291591971626450262144814424411172618188943774725105690851574922374544865628890948773274109561622040022136970632948166009941425683576381155722191980954262373394704682297682490061906408535261437100820855976015526295573831744458528440
c2 = 9041231631916227099296501948589424780380702196870972231114747229225732542137483840187783630590878594711315671224997985975031038623195921968945234067183003568830416719957054703139219879265482072634572699299971785171441858501409377942183918216246312330291820452436486171483461790388518159980027140392750222843449604265528929311978655519463562520038992870162220913137870017065557254099767583925177889051326144499369420594398043223307161794788085369471538477803421726790780799629276012701406231535048423554314287152404245482928538931953627397633165453319078105028671410039195670727134471011040601278722143504641171853743
c3 = 3193069356811106774640161554961405075257002069448498144279061282023129342916422283816661697787316681475161942522570615456264481238277711114193792510286127129056376618422336477707825009085263623755329815306483253646072909132096678270667136193038337386976289222105363398033633185639402128949635525665502328717781718263894690234837016959581149138917064108193064639981137359869717065147934752707676203651598070046066514316196771853484143158367616177332902152347890310640338106015356361617700741042461419248117687350565094928451141103632305400493998164788411031832078388030194992306440474662871408938796429927990102583837
看到题目给出c1,c2,c3就知道是共模攻击,但是没有给e的值,根据三个断言,可以推测e为3。一般的共模攻击有两组加密,但是本题有三组,解密的思路为:
Ⅰ.寻找系数关系:
首先,对于e1,e2,利用扩展欧几里得算法求出x1,y1,使得e1 * x1 +e2 * y1 =gcd(e1,e2),然后,对于gcd(e1,e2)(记为e12)和e3,再次利用扩展欧几里得算法求出x2,y2,使得e12 * x2+ e3 *y2=gcd(e12,e3)
Ⅱ.恢复明文
首先,c12 =pow(c1,x1,n) * pow(c2,y1,n) % n
其次,c123 = pow(c12,x2,n) * pow(c3,y2,n) % n
具体解密代码如下:
import gmpy2
from Crypto.Util.number import *
p = 167710954518007348037383082265231465648795974011761905177264545864288011527333715495850532989338171489309608848431113452814709692343039027970312735521415071265608660628968391884287240987858607818275329135585153511665148279408708087727501421558738163577629329044315775019460018956186674179846621352371150072281
q = 130354329753344570838569091064852072757046774566775609047544069941246798511317343102715733555464772099991834579660053860799207243561908291522943696711982657846373844514551117658179060004064010647453939332217996817580433587341521331941287365948919907797478197717562721233289937471168288241937022054501586986443
c1 = 2560344169447809042170685026483682125499025654554670516499742981486615082413150123244985585751880264831112089324011804397189638172356179296987581738515619297036118472798499254785110885662931526277474101787493114656242031264678448394380651657330967744585361662315313462698221954777506355498445242300193032704972074020068699180111637362566860530694807230108024167631423062629721393506643291591971626450262144814424411172618188943774725105690851574922374544865628890948773274109561622040022136970632948166009941425683576381155722191980954262373394704682297682490061906408535261437100820855976015526295573831744458528440
c2 = 9041231631916227099296501948589424780380702196870972231114747229225732542137483840187783630590878594711315671224997985975031038623195921968945234067183003568830416719957054703139219879265482072634572699299971785171441858501409377942183918216246312330291820452436486171483461790388518159980027140392750222843449604265528929311978655519463562520038992870162220913137870017065557254099767583925177889051326144499369420594398043223307161794788085369471538477803421726790780799629276012701406231535048423554314287152404245482928538931953627397633165453319078105028671410039195670727134471011040601278722143504641171853743
c3 = 3193069356811106774640161554961405075257002069448498144279061282023129342916422283816661697787316681475161942522570615456264481238277711114193792510286127129056376618422336477707825009085263623755329815306483253646072909132096678270667136193038337386976289222105363398033633185639402128949635525665502328717781718263894690234837016959581149138917064108193064639981137359869717065147934752707676203651598070046066514316196771853484143158367616177332902152347890310640338106015356361617700741042461419248117687350565094928451141103632305400493998164788411031832078388030194992306440474662871408938796429927990102583837
phi=(p-1)*(q-1)
n=p * q
e1 = pow(3,65537,phi)
e2 = pow(5,65537,phi)
e3 = pow(7,65537,phi)
e12,x1,y1=gmpy2.gcdext(e1,e2)
print("e12=",e12)
print("x1=",x1)
print("y1=",y1)
#发现y1小于0,则先求c2的乘法逆元
c2=gmpy2.invert(c2,n)
y1=-y1
c12=pow(c1,x1,n)*pow(c2,y1,n) % n
e123,x2,y2=gmpy2.gcdext(e12,e3)
print("e123=",e123)
print("x2=",x2)
print("y2=",y2)
m=pow(c12,x2,n)*pow(c3,y2,n) % n
print(long_to_bytes(m))
例题2:
题目:
import gmpy2
from Crypto.Util.number import *
import uuid
flag = b"flag{"+str(uuid.uuid4()).encode()+b"}"
m = bytes_to_long(flag)
p = getStrongPrime(1024)
q = getStrongPrime(1024)
n1 = p * q
n2 = p * q
e1 = 2333
e2 = 0x2333
assert GCD(e1,e2)==1
c1 = pow(m, e1, n1)
c2 = pow(m, e2, n2)
print("n1 =",n1)
print("n2 =",n2)
print("e1 =",e1)
print("e2 =",e2)
print("c1 =",c1)
print("c2 =",c2)
'''
n1 = 25977434245383213061502496098095465491298593274819892066680142309644604447122213990193649136640792045616043244452359563096681308111786639428720577613208873073208345373399185801097504934529486981943138422062519093084571490989920108900165063768027454172383479340269594705161727160665663784155005546900956290823300194993982080817820176683256899248006819975050544361436011973694569861482116060287819754562815300267132104496249550156359417476864266926873511338883992689905817979797654219916643111997131400074229578490338679081091020589498111095229814729232804557730207461328006855958086611451644501518923369121332282446387
n2 = 25977434245383213061502496098095465491298593274819892066680142309644604447122213990193649136640792045616043244452359563096681308111786639428720577613208873073208345373399185801097504934529486981943138422062519093084571490989920108900165063768027454172383479340269594705161727160665663784155005546900956290823300194993982080817820176683256899248006819975050544361436011973694569861482116060287819754562815300267132104496249550156359417476864266926873511338883992689905817979797654219916643111997131400074229578490338679081091020589498111095229814729232804557730207461328006855958086611451644501518923369121332282446387
e1 = 2333
e2 = 0x2333
c1 = 18485676710986119075173536683686462950263457469331993885761169971214128938032438063231897522845618680375729397028835700363169782372594587099048372908212345790811034629235715272689844039455428850999889426940076877552005174718119690829981655533087526118363975468542716361201641751206611729446725223668335826884543868459078761494737060952796969364730619523110915396112202826020259561117145528032775008508084399606014601141698178821709270288546823847725591199659655029049623145505102599794072348396882393484944750435097930829667964115769696899896453970102851438725866601300114175722160091587885920442620806302225997894178
c2 = 16695364664928581532800627548063845285532382094248770791332184106311111465138692453038543176627867352470844455051476759173301213222665138578557853047169090740483130873450630219045786462114849315733985964814297323071258057067338599104261584932140969238868725551762047861055560927674158814431522126509606052082877955899865835628409554581388612342235123760360863332450664084011638284740583896249409211202260177051437402683756328647008719984689105698475757077859180489424704827694801729848236720022267059771816763723353599632989669237797090397186374989429083807476909642056936466992945632706494532552043613399250805214165
'''
解密代码如下:
import gmpy2
from Crypto.Util.number import long_to_bytes
n = 25977434245383213061502496098095465491298593274819892066680142309644604447122213990193649136640792045616043244452359563096681308111786639428720577613208873073208345373399185801097504934529486981943138422062519093084571490989920108900165063768027454172383479340269594705161727160665663784155005546900956290823300194993982080817820176683256899248006819975050544361436011973694569861482116060287819754562815300267132104496249550156359417476864266926873511338883992689905817979797654219916643111997131400074229578490338679081091020589498111095229814729232804557730207461328006855958086611451644501518923369121332282446387
e1=2333
e2 =0x2333
c1 = 18485676710986119075173536683686462950263457469331993885761169971214128938032438063231897522845618680375729397028835700363169782372594587099048372908212345790811034629235715272689844039455428850999889426940076877552005174718119690829981655533087526118363975468542716361201641751206611729446725223668335826884543868459078761494737060952796969364730619523110915396112202826020259561117145528032775008508084399606014601141698178821709270288546823847725591199659655029049623145505102599794072348396882393484944750435097930829667964115769696899896453970102851438725866601300114175722160091587885920442620806302225997894178
c2 = 16695364664928581532800627548063845285532382094248770791332184106311111465138692453038543176627867352470844455051476759173301213222665138578557853047169090740483130873450630219045786462114849315733985964814297323071258057067338599104261584932140969238868725551762047861055560927674158814431522126509606052082877955899865835628409554581388612342235123760360863332450664084011638284740583896249409211202260177051437402683756328647008719984689105698475757077859180489424704827694801729848236720022267059771816763723353599632989669237797090397186374989429083807476909642056936466992945632706494532552043613399250805214165
_,x,y=gmpy2.gcdext(e1,e2) #注意判断x,y的正负性
# if x<0:
# x=-x
# c1 = gmpy2.invert(c1, n)
# if y<0:
# y=-y
# c2 = gmpy2.invert(c2, n)
print("x=",x)
print("y=",y)
#发现x小于0,先求c1的逆元
c1=gmpy2.invert(c1,n)
x=-x
m=pow(c1,x,n)* pow(c2,y,n) % n
print(long_to_bytes(m))
例题3:(小明文攻击+共模攻击)
题目:
flag = '****************************'
flag = "asfajgfbiagbwe"
p = getPrime(2048)
q = getPrime(2048)
m1 = bytes_to_long(bytes(flag.encode()))
e1*e2 = 3087
n = p*q
print()
flag1 = pow(m1,e1,n)
flag2 = pow(m1,e2,n)
print('flag1= '+str(flag1))
print('flag2= '+str(flag2))
print('n= '+str(n))
c1= 463634070971821449698012827631572665302589213868521491855038966879005784397309389922926838028598122795187584361359142761652619958273094398420314927073008031088375892957173280915904309949716842152249806486027920136603248454946737961650252641668562626310035983343018705370077783879047584582817271215517599531278507300104564011142229942160380563527291388260832749808727470291331902902518196932928128107067117198707209620169906575791373793854773799564060536121390593687449884988936522369331738199522700261116496965863870682295858957952661531894477603953742494526632841396338388879198270913523572980574440793543571757278020533565628285714358815083303489096524318164071888139412436112963845619981511061231001617406815056986634680975142352197476024575809514978857034477688443230263761729039797859697947454810551009108031457294164840611157524719173343259485881089252938664456637673337362424443150013961181619441267926981848009107466576314685961478748352388452114042115892243272514245081604607798243817586737546663059737344687130881861357423084448027959893402445303299089606081931041217035955143939567456782107203447898345284731038150377722447329202078375870541529539840051415759436083384408203659613313535094343772238691393447475364806171594
c2= 130959534275704453216282334815034647265875632781798750901627773826812657339274362406246297925411291822193191483409847323315110393729020700526946712786793380991675008128561863631081095222226285788412970362518398757423705216112313533155390315204875516645459370629706277876211656753247984282379731850770447978537855070379324935282789327428625259945250066774049650951465043700088958965762054418615838049340724639373351248933494355591934236360506778496741051064156771092798005112534162050165095430065000827916096893408569751085550379620558282942254606978819033885539221416335848319082054806148859427713144286777516251724474319613960327799643723278205969253636514684757409059003348229151341200451785288395596484563480261212963114071064979559812327582474674812225260616757099890896900340007990585501470484762752362734968297532533654846190900571017635959385883945858334995884341767905619567505341752047589731815868489295690574109758825021386698440670611361127170896689015108432408490763723594673299472336065575301681055583084547847733168801030191262122130369687497236959760366874106043801542493392227424890925595734150487586757484304609945827925762382889592743709682485229267604771944535469557860120878491329984792448597107256325783346904408
n= 609305637099654478882754880905638123124918364116173050874864700996165096776233155524277418132679727857702738043786588380577485490575591029930152718828075976000078971987922107645530323356525126496562423491563365836491753476840795804040219013880969539154444387313029522565456897962200817021423704204077133003361140660038327458057898764857872645377236870759691588009666047187685654297678987435769051762120388537868493789773766688347724903911796741124237476823452505450704989455260077833828660552130714794889208291939055406292476845194489525212129635173284301782141617878483740788532998492403101324795726865866661786740345862631916793208037250277376942046905892342213663197755010315060990871143919384283302925469309777769989798197913048813940747488087191697903624669415774198027063997058701217124640082074789591591494106726857376728759663074734040755438623372683762856958888826373151815914621262862750497078245369680378038995425628467728412953392359090775734440671874387905724083226246587924716226512631671786591611586774947156657178654343092123117255372954798131265566301316033414311712092913492774989048057650627801991277862963173961355088082419091848569675686058581383542877982979697235829206442087786927939745804017455244315305118437
解密代码入下:
import gmpy2
from Crypto.Util.number import long_to_bytes
c1= 463634070971821449698012827631572665302589213868521491855038966879005784397309389922926838028598122795187584361359142761652619958273094398420314927073008031088375892957173280915904309949716842152249806486027920136603248454946737961650252641668562626310035983343018705370077783879047584582817271215517599531278507300104564011142229942160380563527291388260832749808727470291331902902518196932928128107067117198707209620169906575791373793854773799564060536121390593687449884988936522369331738199522700261116496965863870682295858957952661531894477603953742494526632841396338388879198270913523572980574440793543571757278020533565628285714358815083303489096524318164071888139412436112963845619981511061231001617406815056986634680975142352197476024575809514978857034477688443230263761729039797859697947454810551009108031457294164840611157524719173343259485881089252938664456637673337362424443150013961181619441267926981848009107466576314685961478748352388452114042115892243272514245081604607798243817586737546663059737344687130881861357423084448027959893402445303299089606081931041217035955143939567456782107203447898345284731038150377722447329202078375870541529539840051415759436083384408203659613313535094343772238691393447475364806171594
c2= 130959534275704453216282334815034647265875632781798750901627773826812657339274362406246297925411291822193191483409847323315110393729020700526946712786793380991675008128561863631081095222226285788412970362518398757423705216112313533155390315204875516645459370629706277876211656753247984282379731850770447978537855070379324935282789327428625259945250066774049650951465043700088958965762054418615838049340724639373351248933494355591934236360506778496741051064156771092798005112534162050165095430065000827916096893408569751085550379620558282942254606978819033885539221416335848319082054806148859427713144286777516251724474319613960327799643723278205969253636514684757409059003348229151341200451785288395596484563480261212963114071064979559812327582474674812225260616757099890896900340007990585501470484762752362734968297532533654846190900571017635959385883945858334995884341767905619567505341752047589731815868489295690574109758825021386698440670611361127170896689015108432408490763723594673299472336065575301681055583084547847733168801030191262122130369687497236959760366874106043801542493392227424890925595734150487586757484304609945827925762382889592743709682485229267604771944535469557860120878491329984792448597107256325783346904408
n= 609305637099654478882754880905638123124918364116173050874864700996165096776233155524277418132679727857702738043786588380577485490575591029930152718828075976000078971987922107645530323356525126496562423491563365836491753476840795804040219013880969539154444387313029522565456897962200817021423704204077133003361140660038327458057898764857872645377236870759691588009666047187685654297678987435769051762120388537868493789773766688347724903911796741124237476823452505450704989455260077833828660552130714794889208291939055406292476845194489525212129635173284301782141617878483740788532998492403101324795726865866661786740345862631916793208037250277376942046905892342213663197755010315060990871143919384283302925469309777769989798197913048813940747488087191697903624669415774198027063997058701217124640082074789591591494106726857376728759663074734040755438623372683762856958888826373151815914621262862750497078245369680378038995425628467728412953392359090775734440671874387905724083226246587924716226512631671786591611586774947156657178654343092123117255372954798131265566301316033414311712092913492774989048057650627801991277862963173961355088082419091848569675686058581383542877982979697235829206442087786927939745804017455244315305118437
e1=2
for e1 in range(2,3087):
if (3087 % e1 ==0):
e2=3087//e1
s0,x,y=gmpy2.gcdext(e1,e2)
m=pow(c1,x,n) * pow(c2,y,n) % n
m0=gmpy2.iroot(m,s0)[0]
print(long_to_bytes(m0))
注意:当gcd(e1,e2) !=1时,最后要开gcd(e1,e2)次方,才是结果
补充:
如果不用gmpy2中的gcdext()函数
可用以下代码代替:
def gcdext(a, b):
if b == 0:
return (a, 1, 0)
# 当b为0时,最大公约数就是a,此时满足ax + by = gcd(a,b)的系数x为1,y为0
else:
g, x1, y1 = gcdext(b, a % b)
# 递归调用,先求下一层的gcd以及对应系数
x = y1
y = x1 - (a // b) * y1
# 根据扩展欧几里得算法推导来更新当前层的系数
return (g, x, y)
3.共享素数攻击
攻击原理:
存在两个密钥对,其中n1=p * q1,n2=p * q2,若已知n1,n2,则可通过gcd(n1,n2),求得共享素数p,再按照常规方法解,最后求明文时,先解密第二次的加密,再用第二次的解密结果继续解密
例题:
题目:
from Crypto.Util.number import *
from flag import *
n1 = 103835296409081751860770535514746586815395898427260334325680313648369132661057840680823295512236948953370895568419721331170834557812541468309298819497267746892814583806423027167382825479157951365823085639078738847647634406841331307035593810712914545347201619004253602692127370265833092082543067153606828049061
n2 = 115383198584677147487556014336448310721853841168758012445634182814180314480501828927160071015197089456042472185850893847370481817325868824076245290735749717384769661698895000176441497242371873981353689607711146852891551491168528799814311992471449640014501858763495472267168224015665906627382490565507927272073
e = 65537
m = bytes_to_long(flag)
print(m)
c = pow(m, e, n1) # c=(m^e)%n1
c = pow(c, e, n2) # c=(c^e)%n2
print(c)
'''
c = 60406168302768860804211220055708551816238816061772464557956985699400782163597251861675967909246187833328847989530950308053492202064477410641014045601986036822451416365957817685047102703301347664879870026582087365822433436251615243854347490600004857861059245403674349457345319269266645006969222744554974358264
'''
题目已知n1.n2,求两者的最大公因数,即为p
具体解密代码如下:
import gmpy2
from Crypto.Util.number import long_to_bytes
n1 = 103835296409081751860770535514746586815395898427260334325680313648369132661057840680823295512236948953370895568419721331170834557812541468309298819497267746892814583806423027167382825479157951365823085639078738847647634406841331307035593810712914545347201619004253602692127370265833092082543067153606828049061
n2 = 115383198584677147487556014336448310721853841168758012445634182814180314480501828927160071015197089456042472185850893847370481817325868824076245290735749717384769661698895000176441497242371873981353689607711146852891551491168528799814311992471449640014501858763495472267168224015665906627382490565507927272073
e = 65537
c = 60406168302768860804211220055708551816238816061772464557956985699400782163597251861675967909246187833328847989530950308053492202064477410641014045601986036822451416365957817685047102703301347664879870026582087365822433436251615243854347490600004857861059245403674349457345319269266645006969222744554974358264
p = gmpy2.gcd(n1,n2)
q1 = n1 // p
q2 = n2 // p
phi_n1 = (p-1)*(q1-1)
phi_n2 = (p-1)*(q2-1)
d1 = gmpy2.invert(e,phi_n1)
d2 = gmpy2.invert(e,phi_n2)
m0 = pow(c,d2,n2)
m1 =pow(m0,d1,n1)
print(long_to_bytes(m1))
4.维纳攻击
攻击原理:
e太大或太小,则通过连分数展开式恢复私钥d
因为e * d mod φ(n) = 1
那么,e * d = 1+ k * φ(n)(左右同时除以d * φ(n))
e/φ(n) = k /d +1/d * φ(n)
又因为φ(n) =(p-1) * (q-1) =p*q -(p+q) +1,且p,q很大
所以p * q>> p+q
所以n = p * q ≈ φ(n)
那么,e / n - k / d = 1 / d * φ(n)
所以k/d与e/n十分接近,将e/n进行连分数展开,再对每一项求渐进分数,通过遍历渐进分数,k/d的值很可能被渐进分数的某一项覆盖
连分数:
连分数是将一个数表示为一个整数与一个分数之和,而这个分数的分母又是一个整数与另一个分数之和,如此不断嵌套下去的形式
表达形式如下:
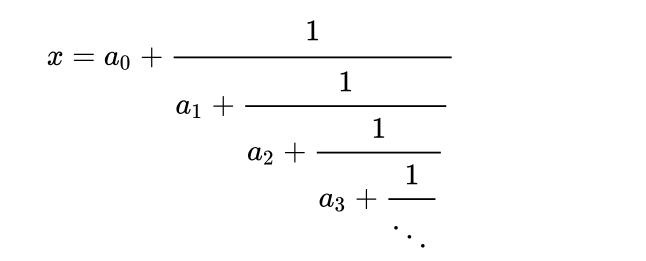
通常简记为[a0,a1,a2,a3,...],其中a0,a1,a2,a3 ...为整数,a0可以是任意整数,而ai(i>=1)一般为正整数
渐进分数:
对于一个连分数[a0,a1,a2,a3...an...],其渐进分数是依次截取连分数的开头部分得到的分数序列。第k个渐进分数记为pk/qk,它是由连分数[a0,a1,a2,a3...ak]计算得到的
计算方法:
设连分数为[a0,a1,a2,...an...],可以通过递推公式来计算渐进分数
初始值:k=0时,p0 = a0,q0=1;k=1时,p1=a0 * a1 +1,q1=a1
k>=2时,pk = ak * p (k-1) +p(k-2),qk = ak *q (k-1) + q (k-2)
例题:
题目:
from secret import flag
from Crypto.Util.number import *
m = bytes_to_long(flag)
p = getPrime(512)
q = getPrime(512) #取个512比特的随机质数
N = p * q
phi = (p-1) * (q-1)
while True:
d = getRandomNBitInteger(200) #生成恰好为200比特的随机数
if GCD(d, phi) == 1:
e = inverse(d, phi)
break
c = pow(m, e, N)
print(c, e, N, sep='\n')
# 37625098109081701774571613785279343908814425141123915351527903477451570893536663171806089364574293449414561630485312247061686191366669404389142347972565020570877175992098033759403318443705791866939363061966538210758611679849037990315161035649389943256526167843576617469134413191950908582922902210791377220066
# 46867417013414476511855705167486515292101865210840925173161828985833867821644239088991107524584028941183216735115986313719966458608881689802377181633111389920813814350964315420422257050287517851213109465823444767895817372377616723406116946259672358254060231210263961445286931270444042869857616609048537240249
# 86966590627372918010571457840724456774194080910694231109811773050866217415975647358784246153710824794652840306389428729923771431340699346354646708396564203957270393882105042714920060055401541794748437242707186192941546185666953574082803056612193004258064074902605834799171191314001030749992715155125694272289
解密代码如下:
import gmpy2
import libnum
from Crypto.Util.number import long_to_bytes
def transform(x,y):
#使用辗转相处将分数 x/y 转为连分数的形式
res=[]
while y:
res.append(x//y)
x,y=y,x%y
return res
def continued_fraction(sub_res):
numerator,denominator=1,0
for i in sub_res[::-1]:
#从sublist的后面往前循环 denominator,numerator=numerator,i*numerator+denominator
#将当前的分子作为下一次的分母
return denominator,numerator
#得到渐进分数的分母和分子,并返回
#求解每个渐进分数
def sub_fraction(x,y):
res=transform(x,y)
res=list(map(continued_fraction,(res[0:i] for i in range(1,len(res))))) #将连分数的结果逐一截取以求渐进分数
return res
def get_pq(a,b,c): #由p+q和pq的值通过维达定理来求解p和q
par=gmpy2.isqrt(b*b-4*a*c) #由上述可得,开根号一定是整数,因为有解
x1,x2=(-b+par)//(2*a),(-b-par)//(2*a)
return x1,x2
def wienerAttack(e,n):
for (d,k) in sub_fraction(e,n): #用一个for循环来注意试探e/n的连续函数的渐进分数,直到找到一个满足条件的渐进分数
if k==0:
#可能会出现连分数的第一个为0的情况,排除
continue
if (e*d-1)%k!=0:
#ed=1 (mod φ(n)) 因此如果找到了d的话,(ed-1)会整除 φ(n),也就是存在k使得(e*d-1)//k=φ(n)
continue
phi=(e*d-1)//k #这个结果就是 φ(n)
px,qy=get_pq(1,n-phi+1,n)
if px*qy==n:
p,q=abs(int(px)),abs(int(qy)) #可能会得到两个负数,负负得正未尝不会出现
d=gmpy2.invert(e,(p-1)*(q-1)) #求ed=1 (mod φ(n))的结果,也就是e关于 φ(n)的乘法逆元d
return d
print("该方法不适用")
e = 46867417013414476511855705167486515292101865210840925173161828985833867821644239088991107524584028941183216735115986313719966458608881689802377181633111389920813814350964315420422257050287517851213109465823444767895817372377616723406116946259672358254060231210263961445286931270444042869857616609048537240249
n = 86966590627372918010571457840724456774194080910694231109811773050866217415975647358784246153710824794652840306389428729923771431340699346354646708396564203957270393882105042714920060055401541794748437242707186192941546185666953574082803056612193004258064074902605834799171191314001030749992715155125694272289
d=wienerAttack(e,n)
print("d=",d)
c= 37625098109081701774571613785279343908814425141123915351527903477451570893536663171806089364574293449414561630485312247061686191366669404389142347972565020570877175992098033759403318443705791866939363061966538210758611679849037990315161035649389943256526167843576617469134413191950908582922902210791377220066
m=pow(c,d,n)
print(long_to_bytes(m))
5.rabin加密
特点: e=2
原理:
n= p * q,其中n是公钥,p和q是私钥,p ≡ q ≡ 3 mod 4
加密过程:c = m ^ 2 mod n
解密过程:
mp = c ^ (p+1)/4 mod p
mq = c ^ (q+1)/4 mod q
通过扩展欧几里得算法找到yp,yq
yp * p +yq * q = 1
根据中国剩余定理求4个模n时的平方根:
r1 =(yp * p * mq +yq * q * mp) mod n
r2 = n-r1
r3 = (yp * p *mq - yq * q *mp) mod n
r4 = n-r3
这四个值之一是原始明文,要通过其他已知信息来确定
简单说明:
有断言:x =
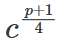
使得 x ** 2 ≡ c mod p
验证以上断言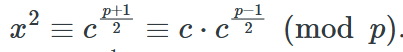
由于有欧拉准则: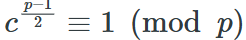
所以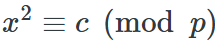 得证
得证
例题:
已知:
p = 13934102561950901579
q = 14450452739004884887
n = 201354090531918389422241515534761536573
c = 20442989381348880630046435751193745753
e = 2
解密代码如下:
import gmpy2
import libnum
p = 13934102561950901579
q = 14450452739004884887
n = 201354090531918389422241515534761536573
c = 20442989381348880630046435751193745753
e = 2
inv_p = gmpy2.invert(p, q) # p在模q下的逆元
inv_q = gmpy2.invert(q, p) # q在模p下的逆元
mp = pow(c, (p + 1) // 4, p)
mq = pow(c, (q + 1) // 4, q)
a = (inv_p * p * mq + inv_q * q * mp) % n
b = n - int(a)
c = (inv_p * p * mq - inv_q * q * mp) % n
d = n - int(c) # 中国剩余定理
# 因为rabin 加密有四种结果,全部列出。
aa = [a, b, c, d]
for i in aa:
print(libnum.n2s(int(i)))
6.按行加密
例题:
已知:
704796792
752211152
274704164
18414022
368270835
483295235
263072905
459788476
483295235
459788476
663551792
475206804
459788476
428313374
475206804
459788476
425392137
704796792
458265677
341524652
483295235
534149509
425392137
428313374
425392137
341524652
458265677
263072905
483295235
828509797
341524652
425392137
475206804
428313374
483295235
475206804
459788476
306220148
{920139713,19}(n=920139713,e=19)
由已知条件,题目给了很多行密文,但是不能通过把所有行组合在一起来解密,而应该按行解密
已知n,首先利用yafu分解,求出p,q,结果如下:

具体解密代码如下:
import gmpy2,codecs
from Crypto.Util.number import long_to_bytes
n = 920139713
p = 49891
q = 18443
e = 19
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
m=""
with open('c.txt','r') as f:
for c in f.readlines():
m += codecs.decode(long_to_bytes(pow(int(c),d,n)))
print(m)
做的过程中,
m += codecs.decode(long_to_bytes(pow(int(c),d,n)))
这句代码弄了好久才弄明白,主要是类型转换的问题,之前做题没怎么注意这个问题,这里具体列一下:
type()函数用于判断数据类型
pow()的结果为gmpy2.mpz类型,即一个大整数
long_to_bytes()函数:如其名,将长整型转换成字节序列(bytes)
codecs.decode()函数:将字节序列转换成字符串类型(str)
encode()函数:将字符串转换成字节类型(str->bytes)
7.p高位攻击
例题:
题目:
e = 0x10001
p>>128<<128 = 0xd1c520d9798f811e87f4ff406941958bab8fc24b19a32c3ad89b0b73258ed3541e9ca696fd98ce15255264c39ae8c6e8db5ee89993fa44459410d30a0a8af700ae3aee8a9a1d6094f8c757d3b79a8d1147e85be34fb260a970a52826c0a92b46cefb5dfaf2b5a31edf867f8d34d2222900000000000000000000000000000000
n = 0x79e0bf9b916e59286163a1006f8cefd4c1b080387a6ddb98a3f3984569a4ebb48b22ac36dff7c98e4ebb90ffdd9c07f53a20946f57634fb01f4489fcfc8e402865e152820f3e2989d4f0b5ef1fb366f212e238881ea1da017f754d7840fc38236edba144674464b661d36cdaf52d1e5e7c3c21770c5461a7c1bc2db712a61d992ebc407738fc095cd8b6b64e7e532187b11bf78a8d3ddf52da6f6a67c7e88bef5563cac1e5ce115f3282d5ff9db02278859f63049d1b934d918f46353fea1651d96b2ddd874ec8f1e4b9d487d8849896d1c21fb64029f0d6f47e560555b009b96bfd558228929a6cdf3fb6d47a956829fb1e638fcc1bdfad4ec2c3590dea1ed3
c = 0x1b2b4f9afed5fb5f9876757e959c183c2381ca73514b1918d2f123e386bebe9832835350f17ac439ac570c9b2738f924ef49afea02922981fad702012d69ea3a3c7d1fc8efc80e541ca2622d7741090b9ccd590906ac273ffcc66a7b8c0d48b7d62d6cd6dd4cd75747c55aac28f8be3249eb255d8750482ebf492692121ab4b27b275a0f69b15baef20bf812f3cbf581786128b51694331be76f80d6fb1314d8b280eaa16c767821b9c2ba05dfde5451feef22ac3cb3dfbc88bc1501765506f0c05045184292a75c475486b680f726f44ef8ddfe3c48f75bb03c8d44198ac70e6b7c885f53000654db22c8cee8eb4f65eaeea2da13887aaf53d8c254d2945691
该类题的解法,不针对本题
解法一:
后方有0填充
#sage
R.<x> = PolynomialRing(Zmod(n),implementation ='NTL')
p = p_high +x
x0 = p.small_roots(X=2 ** 128,beta = 0.1)[0]
print(p_high + x0) #p
解法二:
后方无0填充:
#sage
R.<x> =PolynomialRing(Zmod(n),implementation ='NTL')
p_high = p_high << 128
p = p_high + x
x0 =p.small_roots(X=2^128,beta=0.1)[0]
print(p_high + x0)
解法三:
丢失的位数需要通过计算得出,且后方有0填充
#sage
pbits = 1024 #p的原本位数
kbits = pbits -p_high.nbits()
R.<x> =PolynomialRing (Zmod(n))
p = p_high + x
x0 = p.small_roots(X=2 ^ kbits,beta=0.4)[0]
print(p_high + x0)
解法四:
丢失的位数需要通过计算得出,且后方无0填充
#sage
pbits = 1024
kbits = pbits -p_high.nbits()
p_high =p_high << kbits
R.<x> = PolynomialRing(Zmod(n))
p = p_high + x
x0 = p.small_roots(X=2 ^ kbits,beta=0.4)[0]
print(p_high +x0)
本题通过解法一求出p,后续就是常规的rsa解密


 浙公网安备 33010602011771号
浙公网安备 33010602011771号