RSA常见题型一

RSA的一些常见题型

一.模数分解（题目一般已知n,e,c）

1.爆破

使用脚本直接爆破

注意：爆破出来的值应该为素数

2.在线网站分解

通过在线网站：https://factordb.com/，即可分解出p和q

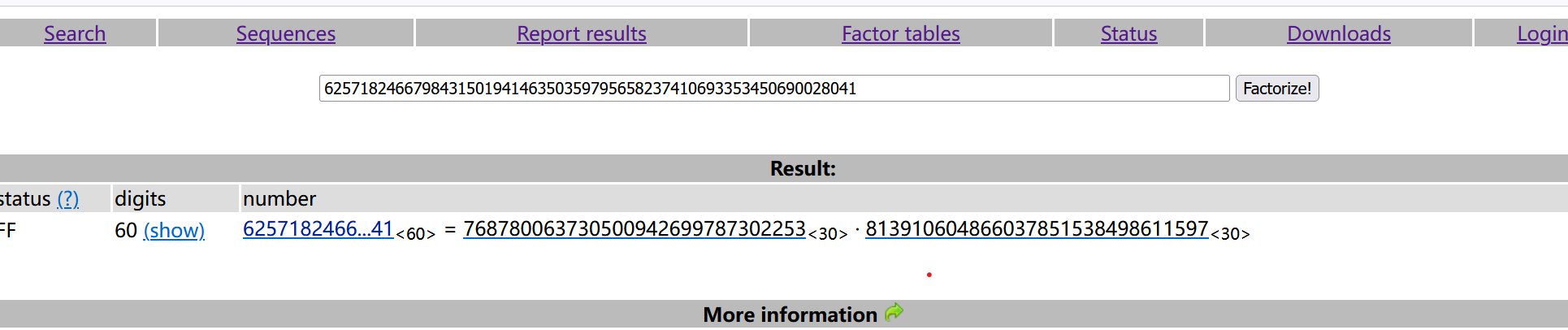
3.yafu分解

使用cmd命令进入yafu所在的目录，或者将目录添加到环境变量中

Ⅰ如果数较小，使用 .\yafu-x64.exe "factor(n)" 命令

Ⅱ如果数比较大，则将模数保存在文本文件中，并将文本文件放在yafu的目录下，例如 n.txt。使用 .\yafu-x64.exe "factor(@)" -batchfile n.txt 命令

（注意事项：文件的最后要换行；使用命令后文件自动消失）

4.例题

题目：

from Crypto.Util.number import getPrime, bytes_to_long
import uuid
flag = "flag{"+str(uuid.uuid4())[:13]+"}"
p = getPrime(100)
q = getPrime(100)
n = p*q
e = 0x10001
m = bytes_to_long(flag.encode())
assert(m < n)
c = pow(m, e, n)
# print(f"flag = {flag}")
print(f"n = {n}")
print(f"c = {c}")
"""
n = 625718246679843150194146350359795658237410693353450690028041c = 118795719073790634455854187484104547013000179946116068066473
"""

观察题目，已知n,e,c,则想到模数分解，用yafu分解，发现n比较大，先把n的值保存到文本文件中（注意换行），再分解

)

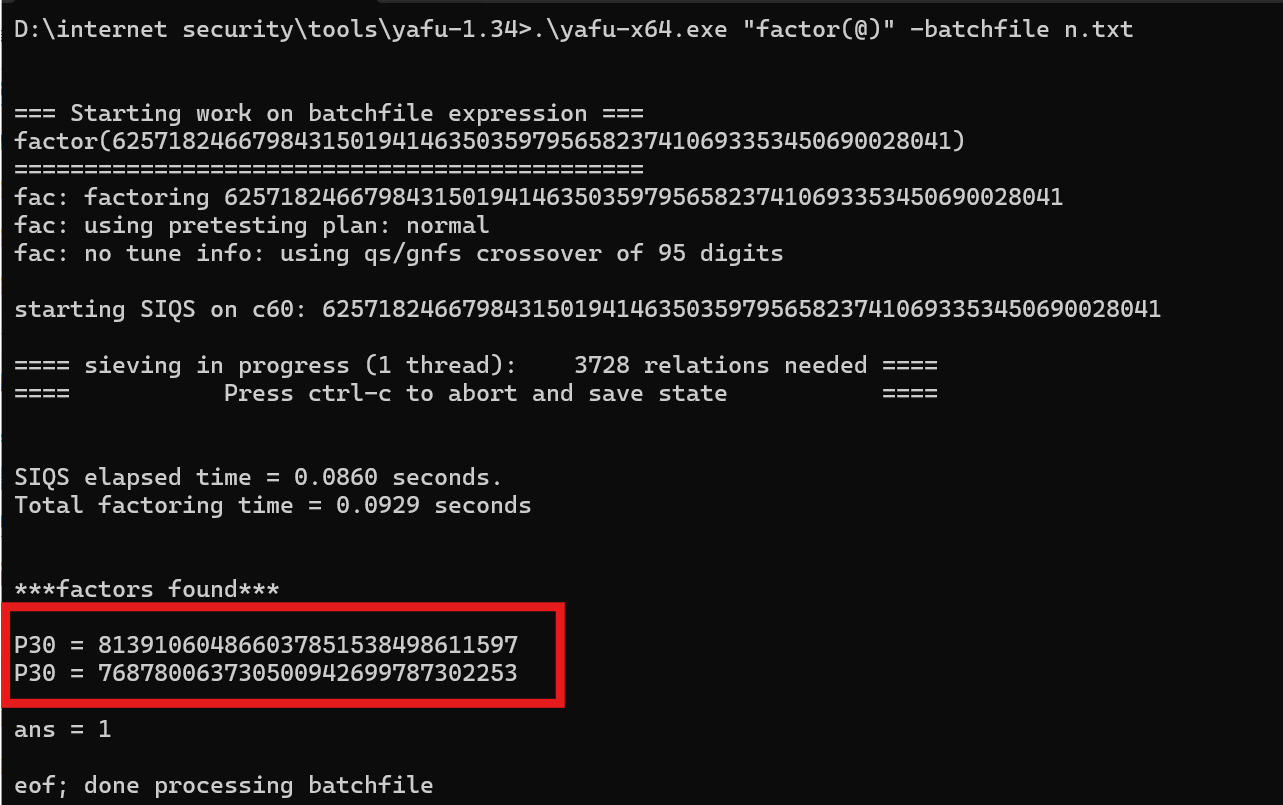
分解得到p和q，后续解密就比较常规了

from Crypto.Util.number import long_to_bytes
import gmpy2
e = 0x10001
p = 768780063730500942699787302253
q = 813910604866037851538498611597
n = p*q
c = 118795719073790634455854187484104547013000179946116068066473
phi_n=(p-1)*(q-1)
d=gmpy2.invert(e,phi_n)
m=pow(c,d,n)
print(long_to_bytes(m))

二.低加密指数攻击（e很小）

在RSA中，e的值一般为65537，但也有的e值很小，然后n很大，这种一般就是低加密指数攻击

原理：当e很小时，c = m^e + kn，我们对k进行爆破，直到c-kn可以对e开根，一开出来就是明文

例题：

题目：

from Crypto.Util.number import *
from flag import flag
assert flag[0:7] == b'moectf{'
assert flag[-1:] == b'}'
flag = flag[7:-1]
assert len(flag) == 32
m1 = bytes_to_long(flag[0:16])
m2 = bytes_to_long(flag[16:32])
def enc1(m):
    p = getPrime(512)
    q = getPrime(512)
    n = p * q
    e = 3
    c = pow(m,e,n)
    return n,e,c
def enc2(m):
    p = getPrime(512)
    q = getPrime(512)
    e = 65537
    d = inverse(e,(p-1)*(q-1))
    n = p * q 
    dp2 = d % (p-1)
    c = pow(m,e,n)
    return n,e,c,dp2
n1,e1,c1 = enc1(m1)
n2,e2,c2,dp2 = enc2(m2)
print("n1="+ str(n1))
print("e1="+ str(e1))
print("c1="+ str(c1))
print("n2="+ str(n2))
print("e2="+ str(e2))
print("c2="+ str(c2))
print("dp2="+ str(dp2))
'''
n1=133024413746207623787624696996450696028790885302997888417950218110624599333002677651319135333439059708696691802077223829846594660086912881559705074934655646133379015018208216486164888406398123943796359972475427652972055533125099746441089220943904185289464863994194089394637271086436301059396682856176212902707
e1=3
c1=1402983421957507617092580232325850324755110618998641078304840725502785669308938910491971922889485661674385555242824
n2=159054389158529397912052248500898471690131016887756654738868415880711791524038820158051782236121110394481656324333254185994103242391825337525378467922406901521793714621471618374673206963439266173586955520902823718942484039624752828390110673871132116507696336326760564857012559508160068814801483975094383392729
e2=65537
c2=37819867277367678387219893740454448327093874982803387661058084123080177731002392119369718466140559855145584144511271801362374042596420131167791821955469392938900319510220897100118141494412797730438963434604351102878410868789119825127662728307578251855605147607595591813395984880381435422467527232180612935306
dp2=947639117873589776036311153850942192190143164329999603361788468962756751774397111913170053010412835033030478855001898886178148944512883446156861610917865
'''

审题，发现flag被分为两个部分，分别进行了加密，第一段就是低加密指数

解密代码如下：

import gmpy2
import binascii
n=gmpy2.mpz(133024413746207623787624696996450696028790885302997888417950218110624599333002677651319135333439059708696691802077223829846594660086912881559705074934655646133379015018208216486164888406398123943796359972475427652972055533125099746441089220943904185289464863994194089394637271086436301059396682856176212902707)
e=3
c=gmpy2.mpz(1402983421957507617092580232325850324755110618998641078304840725502785669308938910491971922889485661674385555242824)
k=0
while True:
	res=gmpy2.iroot(c-k*n,e)
    if(res[1]==True):  
    	print(binascii.unhexlify(hex(res[0])[2:]))
    	break
    k+=1
'''
函数解释：
1.gmpy2.mpz函数:用于创建一个高精度整数对象，可以准确的表示和处理极大的  整数，而不会出现普通整数类型可能会溢出的情况
2.binascii.unhexlify函数:将十六进制（字节类型）数据表示成二进制（字符串）数据
eg:
import binascii
hex_str = b'68656c6c6f'  表示十六进制的字节类型数据，对应 'hello' 的十六进制编码
binary_data = binascii.unhexlify(hex_str)
print(binary_data)  binary_data='hello'
'''

三.dp泄露

dp定义为dp = d mod (p-1)，其中d是 RSA 私钥，p是用于生成n = (p * q)（为另一个大质数）的大质数之一

原理：

dp = d mod (p-1)

dp * e = d * e mod (p-1)

d*e = k1 * (p-1) +dp * e

又因为e * d ≡ 1 mod ϕ(n)

所以 k1 * (p-1) +dp * e = 1 mod ϕ(n)

k1 * (p-1) +dp * e = k2 * (p-1 ) * (q-1) + 1

dp * e = k2 * (p-1 ) * (q-1) +1 - k1 * (p-1)

dp * e = (p-1)* (k2 * (q-1) - k1) + 1

因为dp = d mod (p-1)

所以dp < (p-1)

则e > (k2 * (q-1) - k1)

设x=(k2 * (q-1) - k1) ,则一定存在一个x(1 < x < e) 使得dp * e = (p-1) * x + 1

则p = (dp * e -1) // x + 1

解密代码如下：

import gmpy2
e=65537
n=159054389158529397912052248500898471690131016887756654738868415880711791524038820158051782236121110394481656324333254185994103242391825337525378467922406901521793714621471618374673206963439266173586955520902823718942484039624752828390110673871132116507696336326760564857012559508160068814801483975094383392729
c=37819867277367678387219893740454448327093874982803387661058084123080177731002392119369718466140559855145584144511271801362374042596420131167791821955469392938900319510220897100118141494412797730438963434604351102878410868789119825127662728307578251855605147607595591813395984880381435422467527232180612935306
dp=947639117873589776036311153850942192190143164329999603361788468962756751774397111913170053010412835033030478855001898886178148944512883446156861610917865
for x in range(1,e):
    if(e * dp % x==1):
       p=(e * dp - 1)//x + 1
       if(n % p != 0):
          continue
       q=n//p
       phi_n=(p-1)*(q-1)
       d=gmpy2.invert(e,phi_n)
       m=pow(c,d,n)
       if (len(hex(m)[2:] )% 2 == 1):
#len(hex(m)[2:]对长度做奇偶判断，如果是奇数就跳过后续输出，目的可能是为了保证得到的十六进制字符串能正确地转换为字节数据（因为字节数据对应的十六进制表示通常是偶数长度）
          continue
       print(hex(m)[2:])
       print("flag:",bytes.fromhex(hex(m)[2:]))
#bytes.fromhex()函数用于将十六进制字符串转换为字节类型的数据

四.dp,dq泄露

原理：

m = c ^ d mod n

m = c ^ d + k * n

又因为n = p * q，所以m = c ^ d + k * p * q

左右两边同时对p取模：m1 =m mod p = c ^ d mod p

左右两边同时对q取模：m2 =m mod q = c ^ d mod q

由dp =d mod (p-1)，dq = d mod (q-1)

则d = dp + k1 *(p-1) = dq + k2 * (q-1)

m1 = c ^ (dp + k1 *(p-1)) mod p =(c ^ dp mod p * c ^ k1 *(p-1) mod p) mod p

同理，m2 = c ^ (dp + k2 *(p-1)) mod p =(c ^ dp mod p * c ^ k2 *(p-1) mod p) mod p

由欧拉定理，a ^ ϕ(n) ≡ 1 mod n

所以c ^ k1 *(p-1) mod p=1, c ^ k2 *(p-1) mod p =1

因此，m1 = c ^ dp mod p，m2 = c ^ dq mod q

c ^ d = k * p +m1 = k * q +m2

k * p = m2 - m1 + k * q

k * p =(m1 - m2 ) mod q

因为gcd(p,q) =1，左右两边同时乘p的逆元，k = p` * (m1 - m2 ) mod q

将k的值带入 c ^ d = k * p +m1

c ^ d = m1 + p` * (m1 - m2 ) (mod q) * p

题目：

p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229 
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469 
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929 
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041 
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852

解密代码如下：

import gmpy2
p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852
I = gmpy2.invert(p,q) #求P的逆元
m1 = pow(c,dp,p)
m2 = pow(c,dq,q)
m = (((m1-m2)*I)%q)*p+m1
print(m)                #10进制明文
print(hex(m)[2:])            #16进制明文print(bytes.fromhex(hex(m)[2:]))    #16进制转文本

对于m = (((m1-m2)I)%q)p+m1，我们 通过逆元的定义（eg, e d ≡ 1mod (p-1)（q-1），可以化简为 m=m1+(m2-m1) mod q

新解法，更简单

直接使用中国剩余定理求解

import gmpy2,libnum
from Crypto.Util.number import long_to_bytes

p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852

m1 = pow(c,dp,p)
m2 = pow(c,dq,q)
m= libnum.solve_crt([m1,m2],[p,q])
print(long_to_bytes(m))
#b'noxCTF{W31c0m3_70_Ch1n470wn}'