计算机图形学——投影 pygame演示

模型：

def stereoscopic():
    x1,x2 = -100,100
    y1,y2 = 0,100
    z1,z2 = 1,100
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x1,y1,z1), Coordinate(x2,y1,z1),2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x1,y1,z2), Coordinate(x2,y1,z2),2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x1,y1,z1), Coordinate(x1,y1,z2),2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x2,y1,z1), Coordinate(x2,y1,z2),2)

    pygame.draw.line(screen, (1, 1, 1), Coordinate(x1, y2, z1), Coordinate(x2, y2, z1), 2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x1, y2, z1), Coordinate(x2, y2, z1), 2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x1, y2, z2), Coordinate(x1, y2, z2), 2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x2, y2, z2), Coordinate(x2, y2, z2), 2)

    pygame.draw.line(screen, (1, 1, 1), Coordinate(x1, y1, z1), Coordinate(x1, y2, z1), 2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x2, y1, z1), Coordinate(x2, y2, z1), 2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x1, y1, z2), Coordinate(x1, y2, z2), 2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x2, y1, z2), Coordinate(x2, y2, z2), 2)

stereoscopic()
def stereoscopic2():
    x1,x2 = -100,100
    y1,y2 = 0,100
    z1,z2 = 1,2
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x1,y1,z1), Coordinate(x1,y2,z1),2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x2,y1,z1), Coordinate(x2,y2,z1),2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x1,y1,z1), Coordinate(x2,y1,z1),2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x1,y2,z1), Coordinate(x2,y2,z1),2)

    pygame.draw.line(screen, (1, 1, 1), Coordinate(x1,y1,z2), Coordinate(x1,y2,z2),2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x2,y1,z2), Coordinate(x2,y2,z2),2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x1,y1,z2), Coordinate(x2,y1,z2),2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x1,y2,z2), Coordinate(x2,y2,z2),2)
    #
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x1, y1, z1), Coordinate(x1, y1, z2), 2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x1, y2, z1), Coordinate(x1, y2, z2), 2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x2, y1, z1), Coordinate(x2, y1, z2), 2)
    pygame.draw.line(screen, (1, 1, 1), Coordinate(x2, y2, z1), Coordinate(x2, y2, z2), 2)


# stereoscopic2()

 

 

1，平行投影

　　1.1 ：

　　# 平行投影
　　# a,b,c = 1,1.2,1 #投影方向
　　# x = x-a/c*z
　　# y = y-b/c*z
模型一：正视图，侧视图

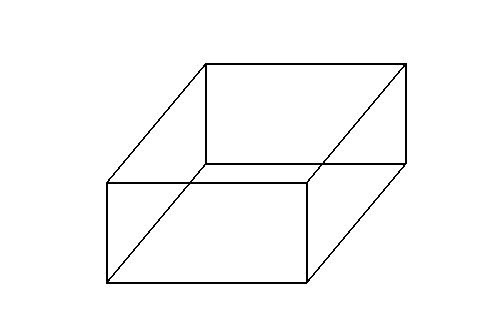
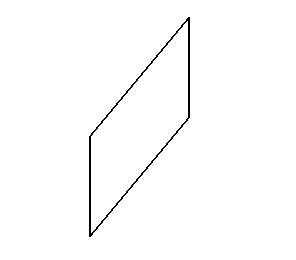
模型二：正视图，侧视图

 

 

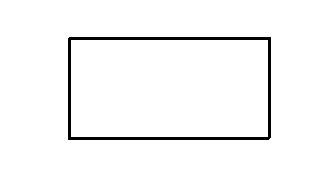
2，斜投影

　　2.1 ：

　　#斜平行投影 
　　# xp,yp,zp = 1,1.5,1 #投影方向矢量
　　# x = x-xp/zp*z
　　# y = y-yp/zp*z

模型一：正视图，侧视图

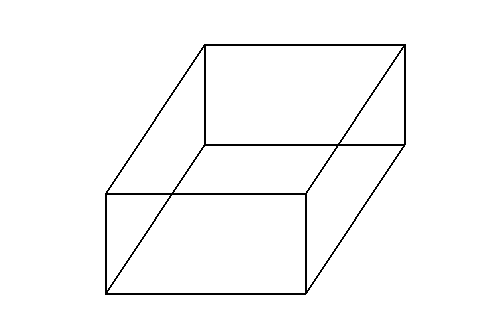
模型二：正视图，侧视图

3，透视投影

　　3.1 投影：

　　　　x/z,y/z

　　　　缺点：不能当z等于零时，无法运算。

模型一：正视图，侧视图

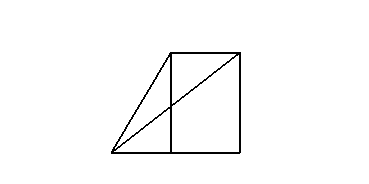
 模型二：正视图，侧视图

 

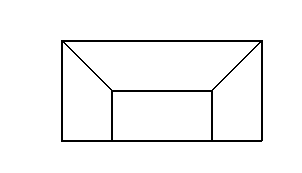
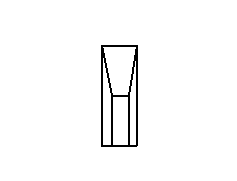
　　3.2视距：

　　　　n：视距　　

　　　　(x*n)/z

　　　　(y*n)/z

　　　　缺点：模型一集中于一点，模型二无空间感

模型一：正视图，侧视图

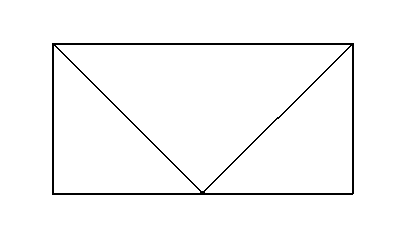
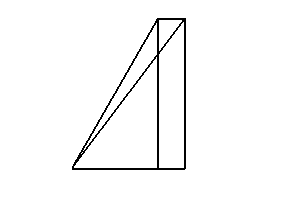
模型二：正视图，侧视图

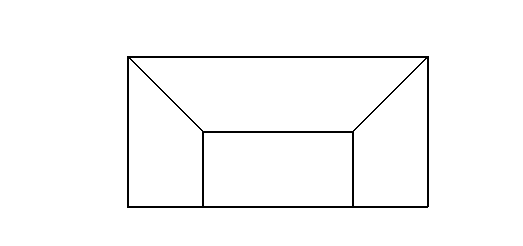
　　3.3视野：