DDPM

Denoising Diffusion Probabilistic Models, DDPM

Ho, Jonathan, Ajay Jain, and Pieter Abbeel. "Denoising diffusion probabilistic models." Advances in Neural Information Processing Systems 33 (2020): 6840-6851.

代码：https://github.com/hojonathanho/diffusion

本篇笔记是出于了解DDPM全文大意之用。下文为全文的大致翻译以及少量理解，不对推导过程展开解释。

Abs

是一种使用扩散概率模型，生成高质量的图像
- 扩散模型：是一类隐变量模型，主要思想来自非平衡热力学 nonequilibrium thermodynamics
本文的模型本质上是在加权变分界上进行训练
- 该变分界是根据扩散概率模型和与Langevin动力学匹配的去噪评分之间的一种新联系设计的
- 是一种渐进的有损解压缩方案，可以被解释为自回归解码的推广。
实验：
- 在无条件CIFAR10数据集上，我们获得了9.46的Inception分数和3.17的最新FID分数。
- 在256x256 LSUN上，我们得到的样品质量与ProgressiveGAN相似。我们的实现可从获得。

Intro

最近，各种深度生成模型在各种各样的数据形式中展示了高质量的样本。生成对抗网络(GANs)、自回归模型、流、变分自编码器(VAEs)合成了引人注目的图像和音频样本[14,27,3,58,38,25,102,32,44,57,26,33,45]，基于能量的建模和评分匹配已经取得显著进展，生成的图像可与GANs的图像相媲美[11,55]。

本文介绍了扩散概率模型[53]的研究进展。扩散概率模型(为方便起见，我们将其称为“扩散模型”)是一种参数化的马尔可夫链，使用变分推理训练、生成与数据分布匹配的样本（在有限时间步内）。模型通过学习马尔科夫链上的状态转移，来逆转扩散过程，这个马尔科夫链指的是：逐步向采样的相反方向的数据添加噪声，直到图片的信号被破坏。当扩散由少量高斯噪声组成时，将采样链上的状态转移操作设置为条件高斯也就足够了，允许特别简单的神经网络参数化。

Transitions of this chain are learned to reverse a diffusion process, which is a Markov chain that gradually adds noise to the data in the opposite direction of sampling until signal is destroyed.
论文将去噪称为 sampling 采样过程，"采样的相反方向"就是正向的加噪声过程。去噪和加噪的过程都是马尔可夫过程。
Markov chain: 节点=状态，边=状态转移。
State: 每个状态是一张图片的格式，但是内容可能是加了很多轮噪声的图片，也可能是完全的随机噪声。
State transition: 状态转移，是一个“operation”，正向时，通过随机采样高斯噪声、加在图片上，完成状态转移操作；反向时，通过一个网络也得到一个高斯噪声，从当前（也是随机采样，但是方差和均值不是随机的，而是学出来的）

扩散模型很容易定义，训练起来也很有效，但就我们所知，还没有证据表明它们能够生成高质量的样本。我们展示了扩散模型实际上能够生成高质量的样本，有时比其他类型生成模型的公布结果更好(第4节)。此外，我们展示了扩散模型的某些参数化揭示了在训练过程中与多个噪声水平上的去噪评分匹配以及在采样过程中与退火的朗日万动力学(第3.2节)的等价性[55,61]。我们使用这个参数化(章节4.2)获得了最好的样本质量结果，因此我们认为这种等价性是我们的主要贡献之一。

a certain parameterization of diffusion models reveals an equivalence with denoising score matching over multiple noise levels during training and with annealed Langevin dynamics during sampling.
a certain parameterization: 对采样的参数化，直接理解为训练的NN输出什么。比如DDPM重参数化的变量是噪声 ε，就是每轮状态转移加上或减去的那个，意味着NN学习的这个噪声的方差和均值。
denoising score matching: 去噪分数匹配【？】意思是这个参数化等价于这个去噪分数匹配。
annealed Langevin dynamics: 退火的朗日万动力学【？】意思是这个参数化等价于这个动力学
实际上推导的数学部分就是推到参数化的一个表示，之后才能建立模型拟合这个参数。NN只是求值的一个工具罢了。

尽管我们的模型具有样本质量，但与其他基于似然的模型相比，我们的模型并没有具有竞争性的对数似然(然而，我们的模型的对数似然优于已报道的基于能量的模型和评分匹配的方法使用的退火重要性抽样大估计?[11,55])。我们发现，我们模型的大部分无损码长都被用来描述难以察觉的图像细节(章节4.3)。我们用有损压缩的语言对这一现象进行了更精细的分析，并表明扩散模型的采样过程是一种渐进式解码，它类似于沿位顺序的自回归解码，极大地推广了自回归模型通常可能实现的解码。

our models do, however, have log likelihoods better than the large estimates annealed importance sampling has been reported to produce for energy based models and score matching.
他们用的是对数似然，并且优于一系列用了 annealed importance sampling 的方法更好。

看完intro 觉得这作者真爱用长句。

Background

background直接看是看不懂的。推荐到知乎上去搜最多赞的一篇专栏文章，LaTex渲染100分。

扩散模型[53]是形式为\(p_\theta(x_0):=\int p_\theta(x_{0:T})dx_{1:T}\) 的隐变量模型，其中\(x_1...x_T\) 是与数据\(x_0 \sim q(x_o)\) 具有相同维数的隐变量。联合分布 \(p_\theta(x_{0:T})\) 被称为反向过程，它被定义为具有学习高斯迁移的马尔可夫链，初始状态为 \(p(x_T)=N(x_T;\bf 0 , I)\):

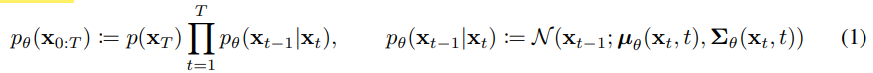
扩散模型与其他类型隐变量模型的区别在于近似后验\(q(x_{1:T}|x_0)\)称为正向过程或扩散过程，被固定在一个马尔可夫链上，根据方差 \(\beta_1,...\beta_T\) 逐步向数据上添加噪声：

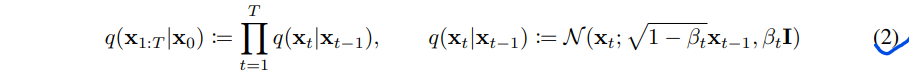
其他类型隐变量模型：指的是VAE、GAN这种；隐变量在VAE中是一个比输入图像低维得多的向量。GAN也类似。Diffusion的隐变量大小=图像，这是比较特别的。

通过在负对数似然上优化通常的变分界来进行训练:

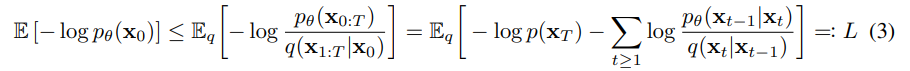
正向过程的方差beta_t可以通过重参数化[33]来学习，或者保持作为超参数的常数，而反向过程的表达在一定程度上是通过在\(p_\theta(x_{t-1}|x_t)\) 中选择高斯条件来保证的，因为当βt比较小[53]时，两个过程具有相同的函数形式。正向过程的一个显著特性是它允许以封闭形式在任意时间步t处对xt进行采样，记\(\alpha_t:=1-\beta_t, \overline \alpha_t:= \prod_{s=1}^t \alpha_s\)，可以得到：

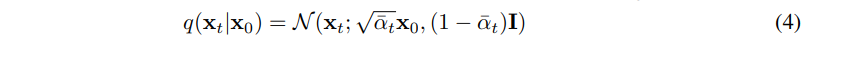
reparameterization 重参数化

因此，一个可能的有效训练方式是：通过随机梯度下降优化\(\cal L\)的随机项。进一步的改进来自方差减少，重写公式(3)中的\(L\)为:

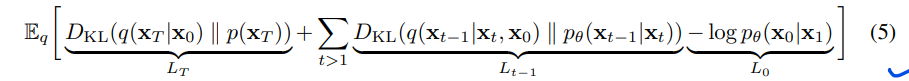
(详见附录A。标签在第3节中有用到)

式(5)利用KL散度直接比较 \(p_\theta(x_{t-1}|x_t)\)与前向过程后验，当以\(x_0\)为条件时，会比较易于处理（下列公式6）:

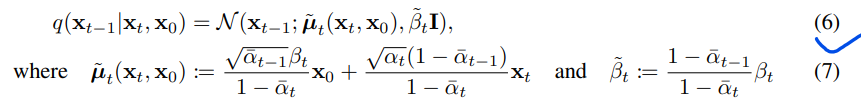
因此，Eq.(5)中的所有KL散度都是高斯量之间的比较，因此它们可以用Rao-Blackwellized的封闭形式表达式来计算，而不是高方差的蒙特卡罗估计。

Rao-Blackwellized Theorem：一种参数估计方法，”…去估计一个参数，在无偏的情况下，Rao-Blackwell的定理下估计出的估计量和该参数的方差最小“

一点疑问是多处出现的 lossless codelength 无损码长，不是很能理解其意。

Diffusion models and denoising autoencoders

扩散模型可能看起来是潜在变量模型的一个受限制的类别，但它们在实现中允许大量的自由度。需要必须选择的有：正向过程的方差\(\beta_t\)，反向过程的模型结构，和反向过程的高斯分布参数化。

如之前讲到的，参数化对象的选择决定学习的模型学习的是什么

为了指导我们的选择，我们在扩散模型和去噪分数匹配之间建立了一个新的显式联系(第3.2节)，这导致了扩散模型的一个简化的加权变分界目标(第3.4节)。最终，我们的模型设计被简单性和实证结果所证明(第4节)。我们的讨论由公式(5)进行分类。

前向过程& \(L_T\)

我们忽略了正向过程方差\(\beta_t\)可以通过重新参数化学习的事实，而是将它们固定为常数(详见第4节)。因此，在我们的实现中，近似后验q没有可学习的参数，所以\(L_r\)在训练过程中是一个常数，可以忽略。

反向过程 & \(L_{1:T-1}\)

现在我们讨论\(L_t\)项：

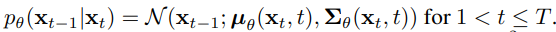
首先，我们设方差为未训练的时间相关常数：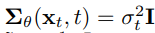

实验上，\(\sigma^2_t=\beta_t\)和 \(\sigma_t^2 = \tilde \beta_t\) 结果相似。
- 对于\(x_0 \sim N(\bf 0, I)\)，第一种选择是最优的；
- 对于确定地将x0设置为一个点?，第二种是最优的。
对于每个坐标的方差为1的数据，这两种选择对应逆向过程熵上下限的两个极限情况。

其中，\(\tilde \beta_t\)为：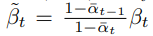

其次，为了表示平均值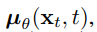，我们提出了一个特定的参数化，其动机是以下对\(L_t\)的分析：

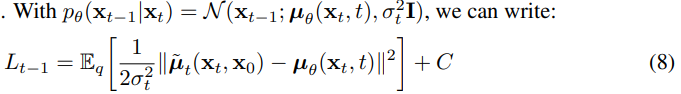
C是一个常数。因此，我们看到\(\mu_\theta\)最直接的参数化是一个预测\(\tilde\mu_t\)的模型，即正向过程后验均值。然而，我们可以通过重新参数化Eq.(4)进一步扩展Eq.(8)为:

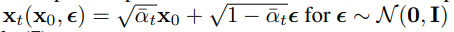
接着应用前向过程后验公式(7):

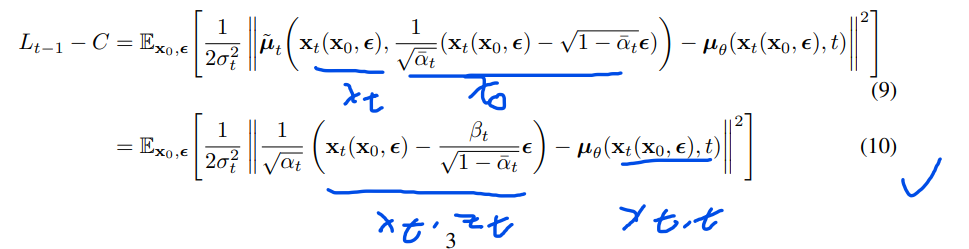
公式10说明，\(\mu_\theta\)必须预测下式：

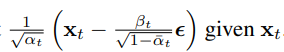
其中xt是输入。我们可以选择参数化：

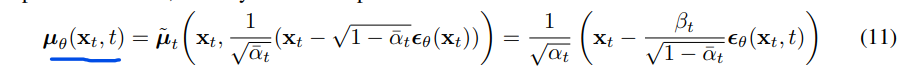
其中\(\epsilon_\theta\)是一个函数逼近器（神经网络），用于从\(x_t\)预测ε。对\(x_{t-1} \sim p_\theta(x_{t-1}|x_t)\) 进行抽样，即计算:

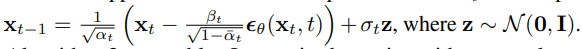
算法2类似于朗之万动力学，将\(\epsilon_\theta\)作为习得的数据密度梯度。此外，通过参数化(11)，式(10)简化为:

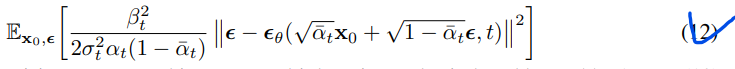
数据缩放、反向过程解码器 & L0

我们假设图像数据由{0,1，…， 255} 线性地放缩到[- 1,1]。这确保了神经网络反向过程在从标准正态先验\(p(x_T)\)开始的一致缩放的输入上运行。为了获得离散对数似然，我们将反转过程的最后一项设置为一个独立的离散decoder，来自高斯分布：

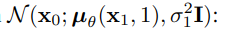
离散过程如下：

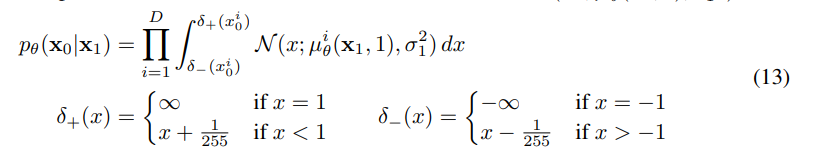
其中D为数据维数，i上标表示提取一个坐标。(相反，一个直接的方法是，合并一个更强大的解码器，如条件自回归模型，但我们把它留给以后的工作。)类似于离散化连续。对于在VAE解码器和自回归模型中使用的分布[34,52]，我们在这里的选择确保了变分界是离散数据的无损码长(codelength)，不需要向数据添加噪声，也不需要将缩放操作的雅可比矩阵合并到对数似然中。在采样结束时，不引入噪声就能得到。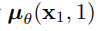

简化的训练目标

用上面定义的反向过程和解码器，变分界，由等式派生的术语组成。(12)和(13)显然对\(\theta\)可微并且可以被应用于训练。然而，我们发现对以下变分界的变体进行训练有利于提高样本质量(也更容易实现):

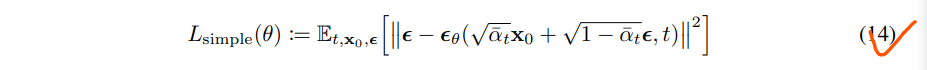
其中t在1和t之间的均匀分布。t = 1的情况对应于L0，离散解码器定义(13)中近似于高斯概率密度函数乘以bin宽度的积分（忽略\(\sigma_1^2\) 、边缘效应）。t > 1的情况对应于式(12)的未加权版本，类似于NCSN去噪评分匹配模型[55]所使用的损失加权。(LT没有出现，因为正向过程方差beta t是固定的。) 算法1显示了这个简化目标下的完整训练过程。

由于我们的简化目标(14)摒弃了式(12)中的权重，因此与标准变分界[18,22]相比，它是一个强调重构不同方面的加权变分界。特别是，我们在第4节中的扩散过程设置使简化的目标降低了对应于小t的损失项的权重。这些项训练网络去噪具有非常少量噪声的数据，因此降低它们的权重是有益的，这样网络就可以专注于更大t项下更难的去噪任务。我们将在我们的实验中看到，这种重新加权导致了更好的样本质量。

看完感觉数学理论方面还是缺门课

实验

为所有实验设置T = 1000，以便抽样过程中所需的神经网络评估数量与之前的工作相匹配[53,55]。我们将正向过程方差设为从β_1 = 10e-4到β_T = 0.02之间线性递增的常数。这些常数被选择为相对于比例为[- 1,1]的数据较小，确保反向和正向过程具有大致相同的函数形式，同时保持在xT处的信噪比尽可能小

为了表示反向过程，我们使用了类似于Unmasked的PixelCNN++[52,48]的U-Net骨干网，在整个过程中使用组归一化 (group normalization)[66]。模型是跨时间共享参数的，时间embedding是通过[60]的Transformer正弦化position embedding的方法，正弦化 time embedding 后输入到网络。我们在16 x 16的特征图分辨率上使用自注意力[63,60]。详情见附录B。

sinusoidal 正弦函数的

采样质量

表1显示了CIFAR10上的Inception评分、FID评分和负对数似然(无损码长?)。我们的FID得分为3.17，我们的无条件模型比文献中的大多数模型(包括类条件模型)获得了更好的样本质量。我们的FID分数是根据训练集计算的，这是标准做法; 当我们相对于测试集计算它时，它的分数是5.24，这仍然优于文献中的许多训练集FID分数。

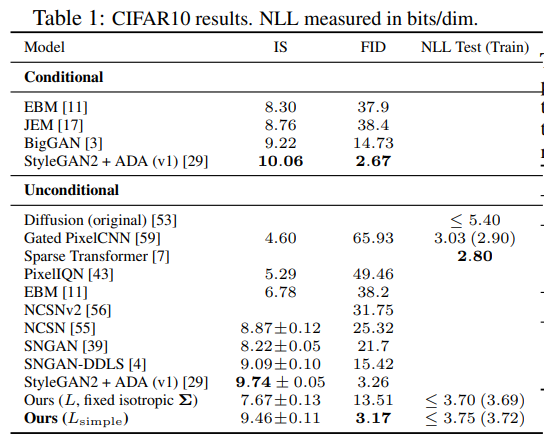
我们发现，正如预期的那样，在真变分界上训练我们的模型比在简化目标上训练产生更好的码长，但后者产生了最好的样本质量。CIFAR10和CelebA-HQ的 256 x 256 样本见图1, LSUN 的 256 x 256 样本见图3和图4[71]，更多见附录D。

反向过程参数化和训练目标的消融实验

如表2，展示了反向过程参数化和训练目标的样本质量影响(第3.2节)。

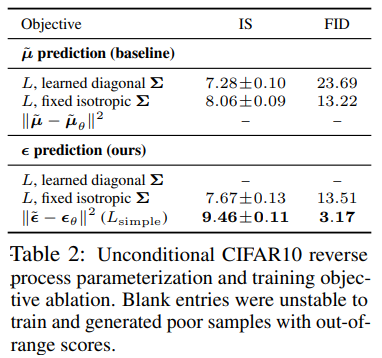
发现：baseline option 即预测\(\tilde \mu\) ，只有在真变分界而不是无加权的均方误差 (类似于式(14)的简化目标)上进行训练时才能很好地工作。
还发现：与固定方差相比，学习反向过程方差(通过参数化将对角线\(\sum_\theta(x_t)\) 纳入变分界) 会导致不稳定的训练和较差的样本质量。正如我们所提出的，在固定方差的变分界上训练时，预测ε的效果与预测 \(\tilde \mu\) 差不多，但在用我们的简化目标训练时效果要好得多。

ε 是噪声，\(\tilde\mu\)是均值

渐进式编码

表1还显示了我们CIFAR10模型的codelengths（？）。训练和测试之间的差距最多为 0.03 bits per dimension?，这与其他基于似然的模型报告的差距相当，表明我们的扩散模型没有过拟合(参见附录D最近邻可视化)。尽管如此，尽管我们的无损码长优于实验大估计的基于能量的模型和退火重要性抽样的得分匹配方法，但它们与其他类型的基于似然的生成模型[7]没有竞争力。

Energy based models:

An energy-based model (EBM) is a form of generative model (GM) imported directly from statistical physics to learning. EBMs provide a unified framework for many probabilistic and non-probabilistic approaches to such learning, particularly for training graphical and other structured models.

An EBM learns the characteristics of a target dataset and generates a similar but larger dataset. EBMs detect the latent variables of a dataset and generate new datasets with a similar distribution

Target applications include natural language processing, robotics and computer vision

Approach:

EBMs capture dependencies by associating an unnormalized probability scalar (energy) to each configuration of the combination of observed and latent variables. Inference consists of finding (values of) latent variables that minimize the energy given a set of (values of) the observed variables. Similarly, the model learns a function that associates low energies to correct values of the latent variables, and higher energies to incorrect values.

Traditional EBMs rely on stochastic gradient-descent (SGD) optimization methods that are typically hard to apply to high-dimension datasets. In 2019, OpenAI publicized a variant that instead used Langevin dynamics (LD). LD is an iterative optimization algorithm that introduces noise to the estimator as part of learning an objective function. It can be used for Bayesian learning scenarios by producing samples from a posterior distribution.

EBMs do not require that energies be normalized as probabilities. In other words, energies do not need to sum to 1. Since there is no need to estimate the normalization constant like probabilistic models do, certain forms of inference and learning with EBMs are more tractable and flexible.[2]

Samples are generated implicitly via a Markov chain Monte Carlo approach. A replay buffer of past images is used with LD to initialize the optimization module.

On image datasets such as CIFAR-10 and ImageNet 32x32, an EBM model generated high-quality images relatively quickly. It supported combining features learned from one type of image for generating other types of images. It was able to generalize using out-of-distribution datasets, outperforming flow-based and autoregressive models. EBM was relatively resistant to adversarial perturbations, behaving better than models explicitly trained against them with training for classification.

由于我们的样本仍然是高质量的，我们得出结论，扩散模型有一个归纳偏差 inductive bias，使它们成为优秀的有损压缩器。将变分界项\(L_1 +..+L_T\)作为rate(压缩率?)，\(L_0\)作为失真，我们的CIFAR10模型具有最高质量的样本，rate=1.78 bits/dim，失真=1.97 bits/dim，这相当于在0到255的范围内的均方根误差为0.95。超过一半的无损码长描述了难以察觉的失真。

渐进有损码

我们可以通过引入一种反映Eq.(5)形式的渐进有损码来进一步探究我们模型的速率失真行为: 参见算法3和算法4，算法3和算法4假设访问一个过程，例如最小随机编码[19,20]，对于任何分布p和q，该过程可以平均使用大约D_KL(g(x) || p(x))位来传输样本x ~ q(x)，而接收方事先只有p是可用的。当应用于x0 ~ q(x0)时，算法3和4传输 x_T，…， x_0序列，使用总期望码长等于式(5)。

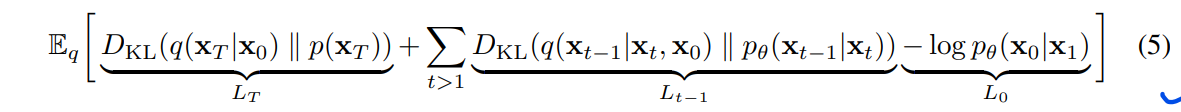
接收方在时间t，具有完全可用的部分信息xt，根据Eq.(4)可以渐进地估计:

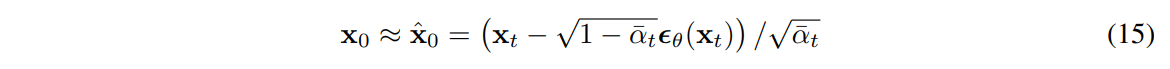
(一个随机构造x0 ~ pθ(x0|xt)也是有效的，但我们在这里不考虑它，因为它使失真更难评估。)

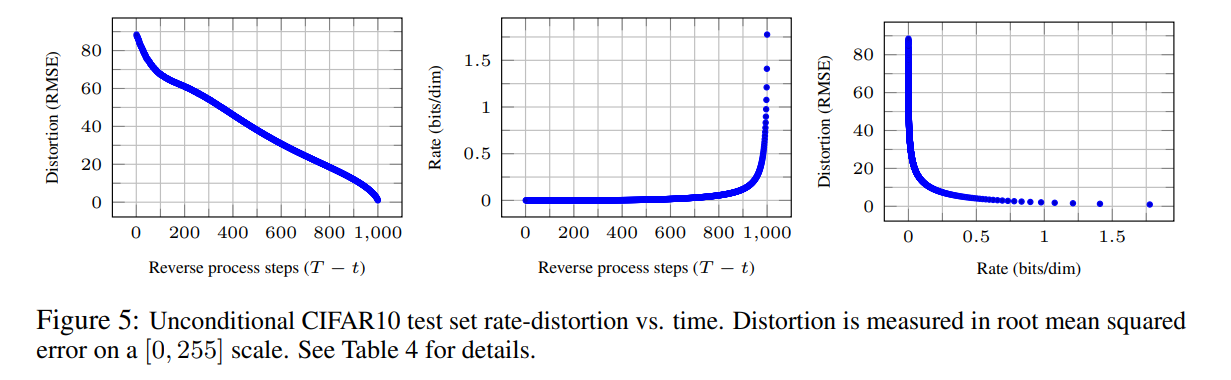
图5显示了在CIFAR10测试集上得到的rate失真图。在每一个时间t，失真计算为均方根误差 \(\sqrt{||x_0 -\hat x_0||^2/D}\)，rate被计算为在时间t时迄今为止接收的比特数的累积。在率失真图的低速率区域，失真急剧下降，说明大部分比特确实分配给了难以察觉的失真。

渐进式生成

我们也运行一个由随机位的渐进解压缩所给出的渐进无条件生成过程。换句话说，我们预测反向过程的结果 \(\hat x_0\)，同时使用算法2从反向过程中采样。图6和图10显示了反向过程中 \(\hat x_0\) 的结果样本质量。大尺度图像的特征首先出现，细节最后出现。图7显示了随机预测x0~ pθ(x0lxt)，对各种t冻结了xt。当t很小时，除细微细节外的所有细节都保留了下来，当t很大时，只保留了大尺度的特征。也许这些是概念性压缩[18]的暗示。

和自回归解码的联系

变分下界(5)可以写为：

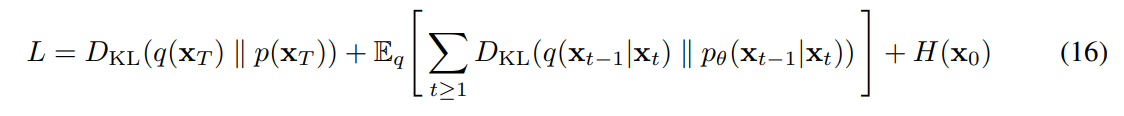
(推导见附录A。)现在考虑将扩散过程长度T设置为数据的维度，定义正向过程，使q(xt|xo)将所有概率质量放在x0上，将前t个坐标屏蔽掉(即 q(xt|xt -1)屏蔽掉第t个坐标)，将p(xT)设置为将所有质量放在空白图像上，为了便于讨论，将pθ(xt-1|xt)设置为一个完全表达的条件分布。

有了这些选择，D_KL(q(xT) || p(xT)) = 0，并且最小化D_KL(q(x -1|xt) Il pθ(xt-1|xt))训练pθ复制坐标 t + 1，…， T不变，给定t+1, …T坐标，预测第t个坐标。因此，用这种特殊的扩散训练pθ就是训练一个自回归模型。

因此，我们可以将高斯扩散模型(2)解释为一种具有广义比特顺序bit ordering的自回归模型，它不能通过重新排序数据坐标来表示。先前的工作表明，这种重排序引入了对样本质量[38]有影响的归纳偏差，因此我们推测高斯扩散也有类似的目的，可能效果更大，因为高斯噪声可能比遮蔽噪声更自然地添加到图像中。此外，高斯扩散长度不受数据维数的限制; 例如，我们使用T = 1000，它小于我们实验中32 x 32 x 3或256 x 256 x 3图像的尺寸。为了快速采样，高斯扩散可以做得更短，为了模型的表达能力，可以做得更长。

插值

用q作为随机编码器，可以将原图像 x0, x0’ ~ q(x0) 插值到隐空间中，得到 xt, xt ~ q(xt |x0)，然后将经过线性插值的图像解码：\(\overline x_t = (1-\lambda)x_0 +\lambda x_0'\)，解码是指：通过逆向过程解码到图像空间中。实际上，我们使用反向过程来去除源图像的线性插值损坏版本中的artifacts。

如图8(左)所示。我们固定了不同lambda值的噪声，所以xt和x'保持不变。图8(右)是对原CelebA-HQ 256 x 256图像(t = 500)的插值和重构。反向过程产生高质量的重建和合理的插值，平滑地改变属性，如姿势，肤色，发型，表情和背景，但不戴眼镜。较大的t会导致更粗糙和更多样的插值，在t = 1000时的新样本(附录图9)。

结论

我们使用扩散模型展示了高质量的图像样本，并发现了扩散模型和变分推理之间的联系，用于训练马尔可夫链、去噪评分匹配和退火的朗日万动力学(以及扩展的基于能量的模型)、自回归模型和渐进有损压缩。由于扩散模型似乎对图像数据具有极好的归纳偏差，我们期待着研究它们在其他数据模式中的效用，以及作为其他类型生成模型和机器学习系统中的组件。

更广泛的影响

我们在扩散模型上的工作与在其他类型的深度生成模型上的现有工作具有相似的范围，例如努力改进GANs的样本质量、流、自回归模型等等。我们的论文代表了在使扩散模型成为这个技术家族中普遍有用的工具方面取得的进展，因此它可能有助于放大生成模型对更广泛的世界已经(和将会)产生的任何影响。不幸的是，生成模型有许多众所周知的恶意使用。为了达到政治目的，可以利用样本生成技术来制作高调人物的虚假图像和视频。虽然在软件工具出现之前很久，人们就已经手动创建了假图像，但像我们这样的生成模型使这一过程更容易。幸运的是，cnn生成的图像目前有一些微妙的缺陷，可以被检测出来[62]，但生成模型的改进可能会使检测变得更加困难。生成模型还反映了训练它们的数据集的偏差。由于许多大型数据集是由自动化系统从互联网上收集的，因此很难消除这些偏差，特别是当图像没有标签时。如果在这些数据集上训练的生成模型样本在互联网上激增，那么这些偏见只会进一步加强。另一方面，扩散模型可能对数据压缩有用，随着数据分辨率的提高和全球互联网流量的增加，这可能对确保广泛受众的互联网可访问性至关重要。我们的工作可能有助于对大量下游任务的未标记原始数据的表示学习，从图像分类到强化学习，扩散模型也可能在艺术、摄影和音乐的创造性应用中变得可行。

posted @ 2022-11-14 21:19 l2f 阅读(1229) 评论(0) 收藏举报

刷新页面返回顶部