2022.9.9课后感想

原码、补码、反码

原码

最高位为符号位，0代表正数，1代表负数，非符号位为该数字绝对值的二进制表示。

如：

127的原码为0111 1111
-127的原码为1111 1111

反码

正数的反码与原码一致；

负数的反码是对原码按位取反，只是最高位(符号位)不变。

如:

127的反码为0111 1111
-127的反码为1000 0000

补码

正数的补码与原码一致；

负数的补码是该数的反码加1。

如：

127的补码为0111 1111
-127的补码为1000 0001

总结一下就是：

1. 正数的原码、反码、补码是一致的；

2. 负数的补码是反码加1，反码是对原码按位取反，只是最高位(符号位)不变；

3. 计算机数字运算均是基于补码的。

补码的好处

如果计算机内部采用原码来表示数，那么在进行加法和减法运算的时候，需要转化为两个绝对值的加法和减法运算；

计算机既要实现加法器，又要实现减法器，代价有点大，那么可不可以只用一种类型的运算器来实现加和减的远算呢？

很容易想到的就是化减为加，举一个生活中的例子来说明这个问题：

时钟一圈是360度，当然也存在365度，但其实它和5度是一样的；

相同的道理，-30度表示逆时针旋转30度，其与顺时针旋转330度是一样的；

这里数字360表示时钟的一圈，在计算机里类似的概念叫模，它可以实现化减为加，本质上是将溢出的部分舍去而不改变结果。

易得，单字节(8位)运算的模为256=2^8。

在没有符号位的情况下，127+2=129，即：

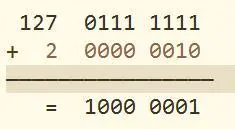
这时，我们将最高位作为符号位，计算机数字均以补码来表示，则1000 0001的原码为减1后按位取反得1111 1111，也就是-127。

也就是说，计算机里的129即表示-127，相当于模256为一圈，顺时针的129则和逆时针127即-127是一样的。

故可以得到以下结论：

负数的补码为模减去该数的绝对值。

如-5的补码为：

-5=256-5=251=1111 1011(二进制)

同样的，临界值-128也可以表示出来：

-128=256-128=128=1000 0000(二进制)

但是正128就会溢出了，故单字节(8位)表示的数字范围为-128--127。

最后，我们来看一下，补码是如何通过模的溢出舍弃操作来完成化减为加的！

16-5=16+(-5)=11

 

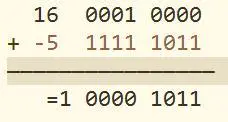
 1 0000 1011将溢出位舍去，得0000 1011(二进制)=11。

随堂实验感想

在第一次JAVA线下课的随堂实验上，我们的任务是

 

 

 

其中第一二阶段比较简单，在第三阶段中括号的加入是最困难的，其中出现的问题有：

1、没有右括号。2、括号只将一个数字扩起。3、有多余的左括号或者右括号。

经过长时间的修改思考，我基本解决了上述问题的并基本完成了任务的要求，唯一不足的是可能会出现将整个式子括住的情况，目前还没有思绪去修改。感到在Java学习上仍有很长的路要走，还有很多的代码练习需要进行。同时这次代码的编写结束后，我意识到了我任务分解的意识不够，在代码编写过程中并未进行任务的分解，导致了代码结构混乱，可读性差，思考困难。要及时加强分解的意识和能力。