1、Batch Normalization

背景：深度神经网络涉及到很多层的叠加，而每一层的参数更新会导致上层的输入数据分布发生变化，通过层层叠加，高层的输入分布变化会非常剧烈，这就使得高层需要不断去重新适应底层的参数更新。Google 将这一现象总结为 Internal Covariate Shift，简称 ICS.

所以ICS是什么呢？将每一层的输入作为一个分布看待，由于底层的参数随着训练更新，导致相同的输入分布得到的输出分布改变了。

机器学习界的炼丹师们最喜欢的数据有什么特点？窃以为，莫过于“独立同分布”了，即independent and identically distributed，简称为 i.i.d. 独立同分布并非所有机器学习模型的必然要求（比如 Naive Bayes 模型就建立在特征彼此独立的基础之上，而Logistic Regression 和 神经网络 则在非独立的特征数据上依然可以训练出很好的模型），但独立同分布的数据可以简化常规机器学习模型的训练、提升机器学习模型的预测能力，已经是一个共识。

机器学习中有个很重要的假设：IID独立同分布假设，就是假设训练数据和测试数据是满足相同分布的，这是通过训练数据获得的模型能够在测试集获得好的效果的一个基本保障。
那么，细化到神经网络的每一层间，每轮训练时分布都是不一致，那么相对的训练效果就得不到保障，所以称为层间的covariate shift。
因此，每个神经元的输入数据不再是“独立同分布”，导致了以下问题：

1、上层网络需要不断适应新的输入数据分布，降低学习速度。
2、下层输入的变化可能趋向于变大或者变小，导致上层落入饱和区，使得学习过早停止。
3、每层的更新都会影响到其它层，因此每层的参数更新策略需要尽可能的谨慎。

 

covariate shift现象以及解决方法：https://blog.csdn.net/guoyuhaoaaa/article/details/80236500

covariate shift现象，指的是训练集的数据分布和预测集的数据分布不一致，这种情况下如果我们在训练集上训练出一个分类器，肯定在预测集上不会取得比较好的效果。这种训练集和预测集样本分布不一致的问题就叫做“covariate shift”现象。比方说，我想训练一个模型根据人的血液样本来判断其有没有得血液病，对于负样本肯定就是收集一些血液病人的血液，但是对于正样本来说的话，其采样一定要合理，所采样例一定要满足整个人群中的分布。如果只采特定领域人群（比方说学校的学生）的血液作为正样本，那么我最终训练得到的模型，很难在所有人群中取得不错的效果，因为真实的预测集中学生只是正常人群中很少的一部分。（这个现象在迁移学习中也很常见）

该用什么样的指标来判断是否已经出现了covariate shift现象？这里使用的指标叫做MCC(Matthews correlation coefficient)，这个指标本质上是用一个训练集数据和预测集数据之间的相关系数，取值在[-1,1]之间，如果是1就是强烈的正相关，0就是没有相关性，-1就是强烈的负相关。

对于Logistic Regression分类器，计算其Mcc值，一般认为如果该值大于0.2，说明预测集和测试集相关度高，也就是说明分类器容易把在训练集上学习到的经验应用在预测集上，也就是说明出现了covariate shift的现象；如果小于0.2，就没有出现covariate shift现象。
Bert是通过巧妙构造预训练任务对网络进行了最大限度的预训练操作，对神经网络参数进行较为合理的参数初始化，然后使用下游任务对神经网络进行微调；而convariate shift说的是训练数据和预测数据分布不一致的问题。之所以在bert或者很多深度学习领域很少遇到covariate shift问题，是因为在训练数据量比较充足的场景下，conariate shift出现的概率是很低的。

 

 

解决思想：

前面说到，出现上述问题的根本原因是神经网络每层之间，无法满足基本假设"独立同分布"，那么思路应该是怎么使得输入分布满足独立同分布。

白化（Whitening）

白化（Whitening）是机器学习里面常用的一种规范化数据分布的方法，主要是PCA白化与ZCA白化。
白化是对输入数据分布进行变换，进而达到以下两个目的：
1、使得输入特征分布具有相同的均值与方差，其中PCA白化保证了所有特征分布均值为0，方差为1；而ZCA白化则保证了所有特征分布均值为0，方差相同；
2、去除特征之间的相关性。
通过白化操作，我们可以减缓ICS的问题，进而固定了每一层网络输入分布，加速网络训练过程的收敛。

Normalization

白化计算成本太高，每一轮训练中的每一层都需要做白化操作；同时白化改变了网络每一层的分布，导致网络层中数据的表达能力受限。因此提出了normalization方法，能够简化计算过程；又能够让数据尽可能保留原始的表达能力。

实际想想，是不是均值方差一致就是相同的分布了呢？其实不一定，normalization这种方式，实际上并不是直接去解决ICS问题，更多的是面向梯度消失等，去加速网络收敛的。类似covariance shift比较直接的解决思路应该是对样本的Reweight操作，根据前后两个分布进行权重的学习，再对新的分布进行reweight。

标准化就是将分布变换为均值方差一致的分布，这么做能够加速收敛的本质是什么呢？在训练过程中，随着网络加深，分布逐渐发生变动，导致整体分布逐渐往激活函数的饱和区间移动，从而反向传播时底层出现梯度消失，也就是收敛越来越慢的原因。

而Normalization则是把分布强行拉回到均值为0方差为1的标准正态分布，使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化，避免梯度消失问题产生，加速收敛。

如果使用标准化，那就相当于把非线性激活函数替换成线性函数了。那么使用非线性激活的意义在哪里呢，多层线性网络跟一层线性网络是等价的，也就是网络的表达能力下降了。

为了保证非线性表达能力，后面又对此打了个补丁，对变换后的满足均值为0方差为1的x进行了scale加上shift操作，形成类似y = s c a l e ∗ x + s h i f t y=scale*x+shifty=scale∗x+shift这种形式，参数通过训练进行学习，把标准正态分布左移或者右移一点，并且长胖一点或者变瘦一点，将分布从线性区往非线性区稍微移动，希望找到一个线性和非线性的较好平衡点，既能享受非线性的较强表达能力，又能够享受线性区较大的下降梯度。

因此，通用的标准化公式如下：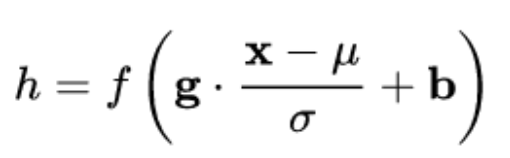

Batch Normalization

BN来自Google在2015年的论文，这也是第一篇normalization的论文，标准化针对输入数据的单一维度进行，根据每一个batch计算均值与标准差

如上，BN针对每个样本$x$的单个维度​$x_i$ ，计算大小为m的mini-batch中的m个$x_i$的均值与方差，以及后续进行再平移及缩放。
但是可以看到，BN针对的是一整个batch进行一阶统计量及二阶统计量的计算，即是隐式的默认了每个batch之间的分布是大体一致的，小范围的不同可以认为是噪音增加模型的鲁棒性，但是如果大范围的变动其实会增加模型的训练难度。
同时，bn在计算过程中，需每一层进行标准化，同时还需要保存统计量，相对来说其内存占用较大，同时也不适用于RNN等网络。

Layer Normalization

LN来自Jimmy Lei Ba等人在2016年发表的论文，为了解决BN的不足之处提出，相对BN的纵向标准化，LN可以称为横向标准化

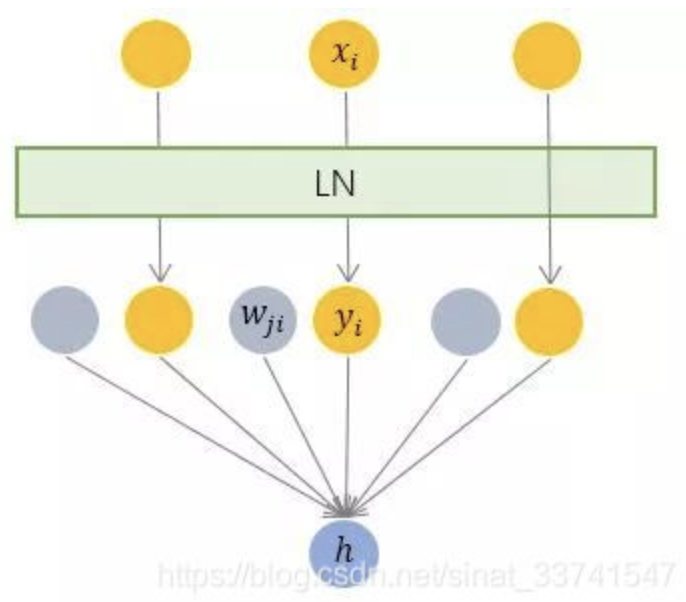
如上，LN根据单个样本计算该层的平均值及方差，之后用同一个再平移及缩放因子规范各位维度的输入。

LN 针对单个训练样本进行，不依赖于其他数据，因此可以避免 BN 中受 mini-batch 数据分布影响的问题，可以用于 小mini-batch场景、动态网络场景和 RNN，特别是自然语言处理领域。此外，LN 不需要保存 mini-batch 的均值和方差，节省了额外的存储空间。

但是，BN 的转换是针对单个神经元可训练的——不同神经元的输入经过再平移和再缩放后分布在不同的区间，而 LN 对于一整层的神经元训练得到同一个转换——所有的输入都在同一个区间范围内。如果不同输入特征不属于相似的类别（比如颜色和大小），那么 LN 的处理可能会降低模型的表达能力。

Weight Normalization  

[https://zhuanlan.zhihu.com/p/350323197]

WN 提出的方案是，将权重向量  分解为向量方向  和向量模  两部分：

其中  是与  同维度的向量， 是欧氏范数，因此 是单位向量，决定了  的方向； 是标量，决定了  的长度。由于  ，因此这一权重分解的方式将权重向量的欧氏范数进行了固定，从而实现了正则化的效果。

假设神经元是简单的线性变换：.

对照一下前述框架：

我们只需令：

就完美地对号入座了！

BN 和 LN 是用输入的特征数据的方差对输入数据进行 scale，而 WN 则是用 神经元的权重的欧氏范式对输入数据进行 scale。虽然在原始方法中分别进行的是特征数据规范化和参数的规范化，但本质上都实现了对数据的规范化，只是用于 scale 的参数来源不同。

Cosine Normalization 

Cosine Normalization 不处理权重向量  ，也不处理特征数据向量  ，就改了一下线性变换的函数：

一定程度上可以理解为，WN 用 权重的模  对输入向量进行 scale，而 CN 在此基础上用输入向量的模  对输入向量进行了进一步的 scale.

 

Normalization有效的原因

1、Normalization 的权重伸缩不变性

权重伸缩不变性（weight scale invariance）指的是，当权重  按照常量  进行伸缩时，得到的规范化后的值保持不变，即：

其中  。

上述规范化方法均有这一性质，这是因为，当权重  伸缩时，对应的均值和标准差均等比例伸缩，分子分母相抵。

权重伸缩不变性可以有效地提高反向传播的效率。

由于

因此，权重的伸缩变化不会影响反向梯度的 Jacobian 矩阵，因此也就对反向传播没有影响，避免了反向传播时因为权重过大或过小导致的梯度消失或梯度爆炸问题，从而加速了神经网络的训练。

权重伸缩不变性还具有参数正则化的效果，可以使用更高的学习率。

由于 

因此，下层的权重值越大，其梯度就越小。这样，参数的变化就越稳定，相当于实现了参数正则化的效果，避免参数的大幅震荡，提高网络的泛化性能。

2、Normalization 的数据伸缩不变性

数据伸缩不变性（data scale invariance）指的是，当数据  按照常量  进行伸缩时，得到的规范化后的值保持不变，即：

其中  。

数据伸缩不变性仅对 BN、LN 和 CN 成立。因为这三者对输入数据进行规范化，因此当数据进行常量伸缩时，其均值和方差都会相应变化，分子分母互相抵消。而 WN 不具有这一性质。

数据伸缩不变性可以有效地减少梯度弥散，简化对学习率的选择。

对于某一层神经元  而言，展开可得

每一层神经元的输出依赖于底下各层的计算结果。如果没有正则化，当下层输入发生伸缩变化时，经过层层传递，可能会导致数据发生剧烈的膨胀或者弥散，从而也导致了反向计算时的梯度爆炸或梯度弥散。

加入 Normalization 之后，不论底层的数据如何变化，对于某一层神经元  而言，其输入  永远保持标准的分布，这就使得高层的训练更加简单。从梯度的计算公式来看：

数据的伸缩变化也不会影响到对该层的权重参数更新，使得训练过程更加鲁棒，简化了对学习率的选择。

 

 

 

原理：可在每层的激活函数前，加入BN，将参数重新拉回0-1正态分布，加速收敛。(理想情况下，Normalize的均值和方差应当是整个数据集的，但为了简化计算，就采用了mini_batch的操作)  

 BN不是简单的归一化，还加入了一个y = γx+β（再平移和再缩放）的操作，用于保持模型的表达能力：Sigmoid 等激活函数在神经网络中有着重要作用，通过区分饱和区和非饱和区，使得神经网络的数据变换具有了非线性计算能力。而第一步的规范化会将几乎所有数据映射到激活函数的非饱和区（线性区），仅利用到了线性变化能力，从而降低了神经网络的表达能力。而进行再变换，则可以将数据从线性区变换到非线性区，恢复模型的表达能力。

*训练与测试：测试时均值和方差不再用每个mini-batch来替代，而是训练过程中每次都记录下每个batch的均值和方差，训练完成后计算整体均值和方差用于测试。

*BN对于Relu是否仍然有效？
有效，学习率稍微设置大一些，ReLU函数就会落入负区间(梯度为0)，神经元就会永远无法激活，导致dead relu问题。BN可以将数据分布拉回来。

*四种主流规范化方法
Batch Normalization(BN): 纵向规范化，针对单个神经元进行，相当于特征维度对同一个batch中所有样本规范化
Layer Normalization(LN): 横向规范化，对于单个样本，综合考虑一层所有维度的输入，计算该层的平均输入值和输入方差，然后用同一个规范化操作来转换各个维度的输入。
Weight Normalization(WN): 参数规范化 对于参数
Cosine Normalization(CN): 余弦规范化 同时考虑参数和x数据

*多卡同步

原因：对于BN来说,用Batch的均值和方差来估计全局的均值和方差,但因此Batch越大越好.但一个卡的容量是有限的,有时可能batch过小,就起不到BN的归一化效果.

原理：利用多卡同步,单卡进行计算后,多卡之间通信计算出整体的均值和方差,用于BN计算, 等同于增大batch size 大小.

 

参考：

https://zhuanlan.zhihu.com/p/33173246 【重点】  https://www.cnblogs.com/shine-lee/p/11989612.html

https://zhuanlan.zhihu.com/p/429901476

https://blog.csdn.net/sinat_33741547/article/details/87158830

https://blog.csdn.net/zxyhhjs2017/article/details/79405591