1.2 关于二分法的一些总结

首先，二分法有前提条件：数组是从小到大排列、数组中没有重复元素。

一般题目会要求：时间复杂度为 O(log n)，这个时候就不能用暴力破解了（因为暴力算法是 O(n)）。

他的原理比较简单：

　　1、定义好数组两边的元素序号后，去循环寻找中间那个元素，同时与要找的元素对比。

　　2、如果中间元素比较大，则寻找的右边界就变种中间元素的左边一个元素，反之则是中间元素的右边一个元素。

　　3、结束的条件是左边序号元素小于等于右边元素的序号（我这里直接按照左闭右闭区间来弄了）

 

完整代码如下：

class Solution {
    public int search(int[] nums, int target) {
        // 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算
        if (target < nums[0] || target > nums[nums.length - 1]) {
            return -1;
        }
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            if (nums[mid] == target)
                return mid;
            else if (nums[mid] < target)
                left = mid + 1;
            else if (nums[mid] > target)
                right = mid - 1;
        }
        return -1;
    }
}

 

注意这里的：

left + ((right -left) >> 1) == (left + right) /2

>>: 二进制右移
举个例子: 1010 >> 1 == 0101
1010 十进制 10
0101 十进制 5
综上 >> 1 作用相当于除二

所以 left + ((right -left) >> 1) ==> left + ((right -left)/2)
==> left + right/2 -left/2 ==> left/2 + right/2 ==> (left + right) /2
注意：>>>是java中的移位运算符,表示无符号右移，而>>是带符号右移。

问题 :为什么不直接用(left + right) /2 而用left + ((right -left) >> 1)
答: 是因为left + right 在某种情况下可能会超过基本类型所能容纳的最大值,而且 >> (位运算) 比 / 运算要快一点

二分法容易犯错的地方：求mid的时候，一定要放在while里面，容易放在外面变成死循环。

下面这里是一些函数的封装方法：

int[] num = {1,2,3,5,4,6};

Arrays.aort(num); //将数组进行排序

int m = Arrays.binarySearch(num, 60);  //寻找是否存在这个数

（注意）

• 如果搜索值是搜索数组里的元素，则返回值大于等于0。因为是从0开始计数。
• 如果搜索值不是搜索数组里的元素，则返回值小于等于0。

---

关于用二分法插入值

（描述：给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。）

具体代码如下：

class Solution {
    public int searchInsert(int[] nums, int target) {
        int n = nums.length;

        // 定义target在左闭右闭的区间，[low, high]
        int low = 0;
        int high = n - 1;

        while (low <= high) { // 当low==high，区间[low, high]依然有效
            int mid = low + (high - low) / 2; // 防止溢出
            if (nums[mid] > target) {
                high = mid - 1; // target 在左区间，所以[low, mid - 1]
            } else if (nums[mid] < target) {
                low = mid + 1; // target 在右区间，所以[mid + 1, high]
            } else {
                // 1. 目标值等于数组中某一个元素  return mid;
                return mid;
            }
        }
        // 2.目标值在数组所有元素之前 3.目标值插入数组中 4.目标值在数组所有元素之后 return right + 1;
        return high + 1;
    }
}

注意！这里最后使用了right，具体原因如下，分别处理如下四种情况，这四种情况就是while循环结束后的情况：

// 目标值在数组所有元素之前 [0, -1]，return right + 1
// 目标值等于数组中某一个元素 return middle;
// 目标值插入数组中的位置 [left, right]，return right + 1
// 目标值在数组所有元素之后的情况 [left, right]， 因为是右闭区间，所以 return right + 1

---

使用二分法来查找目标边界

 描述：给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

代码如下：

class Solution {
    public int[] searchRange(int[] nums, int target) {
        if(nums.length == 0){
            return new int[]{-1,-1};
        }
         if(target<nums[0] || target>nums[nums.length - 1]){
            return new int[]{-1,-1};
        }
        int left = leftBorder(nums, target);
        int right = rightBorder(nums,target);
        if(left==-1){
            return new int[]{-1,-1};
        }
        else{
            return new int[]{left,right};
        }
    }
    public int rightBorder(int[] nums, int target){
        int left = 0, right = nums.length - 1;
        
        while(left<=right){
            int mid = left + ((right - left) >> 1);
            if(nums[mid]>target){
                right = mid - 1;
            }
            else{
                left = mid + 1;
            }
        }
        if(nums[right]==target){
            return right;
        }
        else{
            return -1;
        }
    }

    public int leftBorder(int[] nums, int target){
        int left = 0, right = nums.length - 1;
        while(left<=right){
            int mid = left + ((right - left) >> 1);
            if(nums[mid]<target){
                left = mid + 1;            
            }
            else{
                right = mid - 1;
            }
        }
        if(nums[left]==target){
            return left;
        }
        else{
            return -1;
        }
    }
}

代码难度不大，主要在于判断左右边界，需要判断目标左边界和右边界的范围，要调整left和right，判断他们和mid的范围关系。

这里回顾一下java数组的相关知识：

一、数组的创建

int[] arr = new int[5];//创建数组第一种方式,此时默认值都是为0
arr[0] = 1;//数组的初始化
arr[1] = 2;//数组的初始化
 
int[] arr = new int[]{3,5,1,7};//第二种方式：创建并初始化数组
 
int[] arr = {3,5,1,7};//第三种方式：创建并初始化数组
 
int[] arr;
arr = {1,2,3,4,5};//这种方式是错误的

二、数组内存分析

 

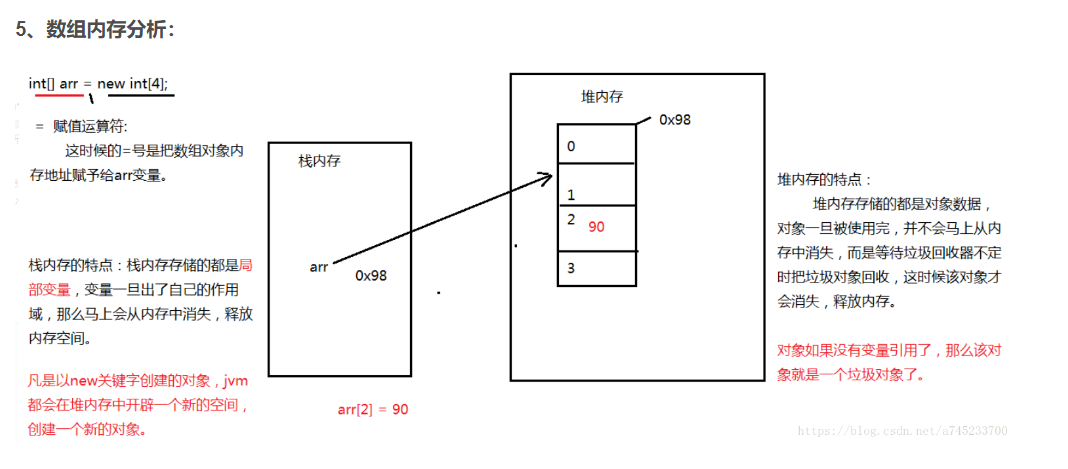
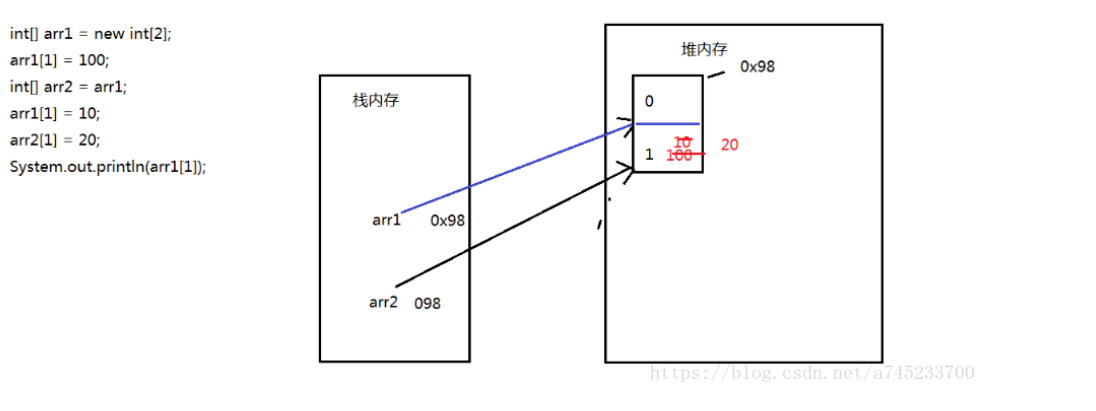
 三、Arrays的使用（持续补充）：

遍历： toString() 将数组的元素以字符串的形式返回

排序： sort() 将数组按照升序排列

查找： binarySearch()在指定数组中查找指定元素，返回元素的索引，如果没有找到返回（-插入点-1） 注意：使用查找的功能的时候，数组一定要先排序。

public static void main(String[] args) {
    int[] array = new int[]{10,30,50,40,60};
    System.out.println(Arrays.toString(array));
        
    Arrays.sort(array);
    System.out.println(Arrays.toString(array));
        
    System.out.println("最小值:"+array[0]+";最大值:"+array[array.length-1]);
        
    int result = Arrays.binarySearch(array, 40);
    System.out.println("目标值的角标："+result);
}

 

---

 

计算一个数的算数平方根（使用二分法查找）

题目描述：

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5

 

解法如下：

class Solution {
    public int mySqrt(int x) {
        int left = 0, right = x/2;
        int mid = 0;
        if(x==0 || x==1) return x;
        while(left<=right){
            mid = left + ((right - left) >> 1);
            if(mid > x/mid){
                right = mid - 1;
            }
            else if(mid < x/mid && (mid+1) > x/(mid+1) || mid == x/mid){
                return mid;
            }
            else{
                left = mid + 1;
            }
        }
        return mid;
    }
}

需要注意的是，这里不用int * int是因为会溢出，一定要注意这个问题。

同时有个知识需要记住：一个数的算术平方根不一定小于这个数的一半。例如，当这个数是0或1时，它的算术平方根等于它本身；当这个数大于1时，它的算术平方根小于这个数的一半。

 

---

 

计算🧮某个数是不是完全平方数

题目描述：

给你一个正整数 num 。如果 num 是一个完全平方数，则返回 true ，否则返回 false 。

完全平方数 是一个可以写成某个整数的平方的整数。换句话说，它可以写成某个整数和自身的乘积。

不能使用任何内置的库函数，如  sqrt 。

 

题目很简单，代码如下：

class Solution {
    public boolean isPerfectSquare(int num) {
        int left = 0, right = num/2;
        int mid = left;
        if(num == 0 || num == 1) return true;
        while(left<=right){
            mid = left + ((right - left) >> 1);
            if(mid == num * 1.0 / mid){
                return true;
            }
            else if(mid > num / mid){
                right = mid - 1;
            }
            else{
                left = mid + 1;
            }
        }
        return false;
    }
}

有些细节需要注意：首先是对于二分法判断的时候，一定要对0和1进行单独提前判断（如果是数组的话是对边界的判断）。然后就是判断的时候，注意5 / 2 = 2，所以需要将结果转换为小数，给被除数*1.0，我发现4.0=4（也就是小数可以和整数进行判断）。

 

二分法暂时告一段落，希望以后回顾能够起到很好的作用。