【题目描述】
原题来自:POJ 3417
Dark 是一张无向图,图中有 NN 个节点和两类边,一类边被称为主要边,而另一类被称为附加边。Dark 有 N–1N–1 条主要边,并且 Dark 的任意两个节点之间都存在一条只由主要边构成的路径。另外,Dark 还有 MM 条附加边。
你的任务是把 Dark 斩为不连通的两部分。一开始 Dark 的附加边都处于无敌状态,你只能选择一条主要边切断。一旦你切断了一条主要边,Dark 就会进入防御模式,主要边会变为无敌的而附加边可以被切断。但是你的能力只能再切断 Dark 的一条附加边。
现在你想要知道,一共有多少种方案可以击败 Dark。注意,就算你第一步切断主要边之后就已经把 Dark 斩为两截,你也需要切断一条附加边才算击败了 Dark。
【输入】
第一行包含两个整数 NN 和 MM;
之后 N–1N–1行,每行包括两个整数 AA 和 BB,表示 AA 和 BB 之间有一条主要边;
之后 MM 行以同样的格式给出附加边。
【输出】
输出一个整数表示答案。
【输入样例】
4 1
1 2
2 3
1 4
3 4
【输出样例】
3
【提示】
数据范围与提示:
对于 20% 的数据,1≤N,M≤1001≤N,M≤100;
对于 100% 的数据,1≤N≤105,1≤M≤2×1051≤N≤105,1≤M≤2×105 。数据保证答案不超过 231−1231−1。
【算法分析】
根据题意,“主要边”构成一棵树,“附加边”则是“非树边”。把一条附加边(x,y)添加到主要边构成的树中,会与树上x,y之间的路径一起形成一个环。如果第一步选择切断x,y之间主要边构成路径上的某条边,那么第二步就必须切断附加边(x,y),才能令Dark被斩为不连通的两部分。 因此,我们称每条附加边(x,y)都把树上x,y之间的路径上的每条边“覆盖了一次”。我们只需统计出每条“主要边”被覆盖了多少次。
若第一步把被覆盖0次的主要边切断,则第二步可任意切断一条附加边。
若第一步把被覆盖1次的主要边切断,则第二步方法唯一。
若第一步把被覆盖2次及2次以上的主要边切断,则第二步无论如何操作都不能击败Dark。
这样我们就得到了击败Dark的方案数。
综上所述,下面我们要解决的问题模型是:给定一张无向图和一棵生成树,求每条“树边”被“非树边”覆盖了多少次。下图左侧的例子中标记了覆盖次数,虚线为“非树边”。

解决此问题有一个经典做法,我们称之为“树上差分算法”。树上差分算法与差分序列的思想类似。
对应在树上,我们给每个节点一个初始为0的权值,然后对每条非树边(x,y),令节点x的权值加1,节点y的权值加1,节点LCA(x,y)的权值减2,如上图右侧的例子所示。
最后对这棵生成树进行一次深度优先遍历,求出F[x]表示以x为根的子树中各节点的权值之和。F[x]就是x与它的父节点之间的“树边”被覆盖的次数。时间复杂度O(N+M)。
我是用树剖做的哟,如果对树剖还不太了解,可以点开下面这个链接看下鸭☟☟☟
这是一个链接(人家才不是莫得感情的链接呢)

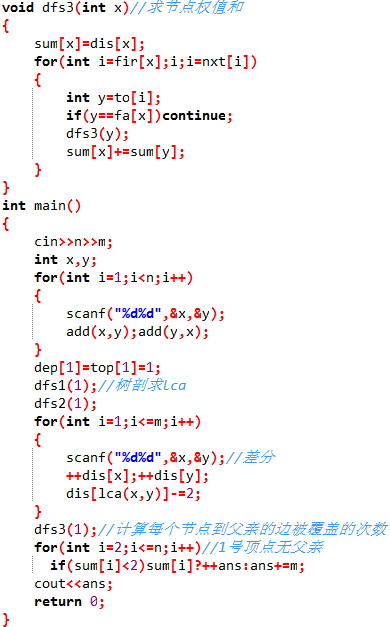
最后送上可复制AC代码(亲测有效(*๓´╰╯`๓))
1 #include<bits/stdc++.h>
2 using namespace std;
3 const int N=1e6+5;
4 int next[2*N],head[N],to[N*2],d[N],add[N],fa[N],sum[N],top[N],size[N],son[N];
5 int n;
6 int m,q,w,ans,p,tot;
7 int read()
8 {
9 int f=1;char ch;
10 while((ch=getchar())<'0'||ch>'9')
11 if(ch=='-')f=-1;
12 int res=ch-'0';
13 while((ch=getchar())>='0'&&ch<='9')
14 res=res*10+ch-'0';
15 return res*f;
16 }
17 void write(int x)
18 {
19 if(x<0)
20 {
21 putchar('-');
22 x=-x;
23 }
24 if(x>9)write(x/10);
25 putchar(x%10+'0');
26 }
27 void ADD(int x,int y)
28 {
29 next[++tot]=head[x];
30 head[x]=tot;
31 to[tot]=y;
32 }
33 int lca(int x,int y)
34 {
35 while(top[x]!=top[y])
36 d[top[x]]>d[top[y]]?x=fa[top[x]]:y=fa[top[y]];
37 return d[x]<d[y]?x:y;
38 }
39 void dfs1(int s)
40 {
41 size[s]=1;
42 for(int i=head[s],t;i,t=to[i];i=next[i])
43 {
44 if(t==fa[s])continue;
45 fa[t]=s;d[t]=d[s]+1;
46 dfs1(t);
47 if(size[t]>size[son[s]])son[s]=t;
48 size[s]+=size[t];
49
50 }
51 }
52 void dfs2(int s)
53 {
54 if(son[s])
55 {
56 top[son[s]]=top[s];
57 dfs2(son[s]);
58 }
59 for(int i=head[s],t;i,t=to[i];i=next[i])
60 {
61 if(!top[t])
62 {
63 top[t]=t;
64 dfs2(t);
65 }
66 }
67 }
68 void dfs3(int s)
69 {
70 sum[s]=add[s];
71 for(int i=head[s],t;i,t=to[i];i=next[i])
72 {
73 if(t!=fa[s])
74 {
75 dfs3(t);
76 sum[s]+=sum[t];
77 }
78 }
79 }
80 int main()
81 {
82 n=read();m=read();
83 for(int i=1;i<n;i++)
84 {
85 int x,y;
86 x=read();y=read();
87 ADD(x,y);
88 ADD(y,x);
89 }
90 top[1]=d[1]=1;
91 dfs1(1);
92
93 dfs2(1);
94 for(int i=1;i<=m;i++)
95 {
96 int x,y;
97 x=read();y=read();
98 add[x]++;add[y]++;add[lca(x,y)]-=2;
99 }
100 dfs3(1);
101 for(int i=2;i<=n;i++)
102 {
103 if(sum[i]<2)sum[i]?ans++:ans+=m;
104 }
105 write(ans);
106 return 0;
107 }
蟹蟹资瓷,请顺手点个“推荐”吧~mua(づ ̄3 ̄)づ╭❤~





 浙公网安备 33010602011771号
浙公网安备 33010602011771号