Boyer–Moore–Horspool文本匹配算法(BM算法的简化版)
英语里有句习语叫"find a needle in a
haystack",译成中文叫"大海捞针"(原意是在一堆干草中寻找一根针)。计算机中的文本匹配(string
matching)就是要解决怎样在一段很长的文本中找到符合要求的一个子串,该子串通常叫模式串(pattern),也就是对应我们要找的“针”。常用
的文本精确匹配(exact string
matching)算法有蛮力法(brute-force),Boyer-Moore算法和KMP算法。后两种算法都是用空间换
时间的经典案例,不像蛮力法,文本的位置指针i不需要回退到已经匹配过的字符位置(BM算法的每次匹配虽然从右向左移动指针,但从来不会将i指针回退到已
经匹配过的字符位置)。在最坏情况下的时间复杂度是与文本长度成线性关系的。特别需要说明的是,BM算法和本文中介绍的它的简化版本Horspool算
法,在最佳情况下的时间复杂度是O(n/m),因此对模式串比较长的情况(比如长度大于5)应用该算法比较有效。
本文介绍Boyer-Moore算法的一个简化版本,叫做Boyer–Moore–Horspool算法或直接叫做Horspool算法。
设文本T长度为n,模式串P长度为m。T的当前位置指针为i(0<=i<n),P的当前位置指针为j(0<=j<m)。
算法:
基本思想是模式串窗口沿着文本向右滑动,但是每次滑动的距离不能太大,否则会冒着遗漏可能成功匹配的字符串的风险。在模式串窗口滑动完成后,开始重新设置
i和j指针,并且让i和j分别从右到左挨个字符匹配。匹配到某个字符位置时发现T[i]和P[j]不相同了(即发现了mismatch,字符T[i]也叫
做bad character),就要分以下三种情况讨论:
1)如果T[i]不在模式串中存在,需要将模式串窗口沿着文本向右滑动j+1个字符位置。这是因为j前面的任何字符P[0..j-1]都与T[i]不匹配,可以直接将P[0]跟i的下一个字符T[i+1]对齐用作下一次的匹配。
例如:
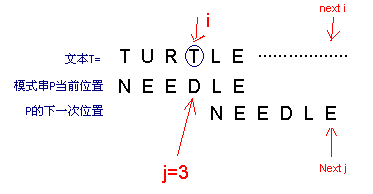
此时j=3,T[i]=T,P[j]=D,但是字符T[i]=T在模式串中没有出现。直接将P[0]=N跟i的下一个字符T [i+1]=L对齐用作下一次的匹配。所以下一次滑动窗口的位置如上所示。
2)如果T[i]在模式串中存在,分两种情况讨论:
case 2a) 设P中最右边出现的字符T[i]所处的位置为q,但是q>j,这时如果还要让T[i]跟P[q]对齐的话,势必要让模式串窗口沿着文本向左移动,显然这是做无用功。所以正确而且最保守的做法是将模式串窗口沿着文本向右移动1个字符位置。
例如:

此时j=4,T[i]=E,P[j]=L,这里字符T[i]=E在模式串中最右边位置q=5(注意必须是最右边位置,左边的两个E不算),因为q=5>j=4,所以最保守的情况是将P只向右滑动一个字符位置,如上图所示。
case 2b)如果q<j (显然q不可能等于j了,因为T[i] != P[j]),这是就需要将T[i]跟P[q]对齐,此时能保证模式串窗口会向右滑动。模式窗口向右滑动的字符个数为j-q。
例如:

此时j=4,T[i]=D,P[j]=L,这里字符T[i]=D在模式串中最右边位置q=3,因为q=3<=j=4,所以将模式窗 口向右滑动j-q=1个字符以保持T[i]=D和j左边的第一个字符D对齐,如上图所示。
注意在下一次匹配时,需要调整j到模式串的末尾字符位置,并且i和j对齐。可用公式得出:
i <- i+m-min(j,1+q)
j <- m -1
二者顺序不能颠倒,因为计算i时需要j的原来值。
根据上面的讨论前提是需要知道q的值,即解决这样一个问题:某个字符c(即bad
character)在模式串P中最右边出现的位置是多少?考虑到文本中这样的c可能为任意字符,需要预先计算一张表(叫做bad- character
shift表, 表的索引值范围即字符集的所有字符值。具体实现时,如果c在模式串中不出现, 该表对应预设值-1。参考下面的实现。
算法复杂度:Horspool算法在平均情况下的时间复杂度是O(n),但是在最坏情况下的复杂度跟蛮力法在同一个数量级,即O(mn),非简化版本的
BM算法在最坏情况下的复杂度是线性O(n)。本博客另外一篇文章将介绍原始的BM算法(BM算法是1977年发明的,而Horspool算法是1980
提出来的)如何在最坏的情况下复杂度跟KMP算法同级即O(n), 。
最坏情况:
例如文本中只含一个字母:T=AAAAAAAAA...AA, 模式串P=BAAA。应用在本算法中的case 2a每次只将模式串沿文本向右滑动一个字符。这跟蛮力法的操作次数一样多。
最佳情况:
文本T=After a long text, here's a needle ZZZZZ
模式串P=ZZZZZ
匹配的过程如下(注意每次i和j指针跳跃距离都是模式串长度m):

实现:
import java.util.Arrays;
/**
*
* @author ljs
* 2011-06-19
*
* 版权说明:可以复制,但须标明出处
*
* Assuming we use ASCII charset
*
*/
public class Horspool {
private static final int CHARSET_SIZE = 256;
//prepare the shift table: find the rightmost position
//in the pattern
private int[] makeShiftTable(String pattern){
int[] shiftTable = new int[CHARSET_SIZE];
//init to -1
for(int i=0;i<CHARSET_SIZE;i++)
shiftTable[i]=-1;
//set the pattern chars
for(int i=0;i<pattern.length();i++){
char c = pattern.charAt(i);
//OK: the rightmost position i may overwrite the left positions
shiftTable[c] = i;
}
return shiftTable;
}
//return the first matched substring's position;
//return -1 if no match
public int match(String text,String pattern){
int n = text.length();
int m = pattern.length();
if(m>n) return -1;
int[] shiftTable = makeShiftTable(pattern);
/****BEGIN TEST: the following code snippet can be commented out****/
System.out.format("%s%n",text);
System.out.format("%s%n",pattern);
/****END TEST: the above code snippet can be commented out****/
int i = m -1;
int j = m -1;
do{
int c = text.charAt(i);
if(c == pattern.charAt(j)){
if(j==0){
//find a match
return i;
}else{
//BM algorithm: move from right to left
i--;
j--;
}
}else{
/****BEGIN TEST: the following code snippet can be commented out****/
int q = shiftTable[c];
int dotsCount = 0;
if(q == -1){//case 1
dotsCount = i+1;
}else if(q>j){ //case 2a
dotsCount = i-j+1;
}else{ //case 2b
dotsCount = i-q;
}
byte dot[] = new byte[dotsCount];
Arrays.fill(dot, (byte)'.');
System.out.format("%s%s%n",new String(dot),pattern);
/****END TEST: the above code snippet can be commented out****/
//determine the i and j for next match attempt
int p = shiftTable[c] + 1;
if(j<=p){
i += m - j;
}else{
i += m - p;
}
j = m - 1;
}
}while(i<=n-1);
//no match
return -1;
}
public static void findMatch(Horspool solver,String text,String pattern){
int index = solver.match(text, pattern);
if(index>=0){
System.out.format("Found at position %d%n",index);
}else{
System.out.format("No match%n");
}
}
public static void main(String[] args) {
Horspool solver = new Horspool();
String text = "A SLOW TURTLE";
String pattern = "NEEDLE";
Horspool.findMatch(solver,text,pattern);
System.out.format("**************%n");
text = "ABCELE";
pattern = "NABDLE";
Horspool.findMatch(solver,text,pattern);
System.out.format("**************%n");
text = "After a long text, here's a needle ZZZZZ";
pattern = "ZZZZZ";
Horspool.findMatch(solver,text,pattern);
System.out.format("**************%n");
text = "The quick brown fox jumps over the lazy dog.";
pattern = "lazy";
Horspool.findMatch(solver,text,pattern);
System.out.format("**************%n");
text = "Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna...";
pattern = "tempor";
Horspool.findMatch(solver,text,pattern);
}
}
测试结果:
A SLOW TURTLE
NEEDLE
......NEEDLE
.......NEEDLE
...........NEEDLE
No match
**************
ABCELE
NABDLE
.NABDLE
No match
**************
After a long text, here's a needle ZZZZZ
ZZZZZ
.....ZZZZZ
..........ZZZZZ
...............ZZZZZ
....................ZZZZZ
.........................ZZZZZ
..............................ZZZZZ
...................................ZZZZZ
Found at position 35
**************
The quick brown fox jumps over the lazy dog.
lazy
....lazy
........lazy
............lazy
................lazy
....................lazy
........................lazy
............................lazy
................................lazy
...................................lazy
Found at position 35
**************
Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna...
tempor
......tempor
............tempor
..................tempor
.....................tempor
...........................tempor
...............................tempor
....................................tempor
..........................................tempor
................................................tempor
......................................................tempor
..........................................................tempor
...........................................................tempor
.................................................................tempor
..................................................................tempor
........................................................................tempor
.........................................................................tempor
Found at position 73




 浙公网安备 33010602011771号
浙公网安备 33010602011771号