数据结构期末复习

cppu版，老师讲的比较简单，所以很简略
重点复习实训

1.数据结构

数据：对客观事物的符号表示：图像、声音等
数据元素：数据段基本单位
数据项：构成数据元素的最小单位
数据对象：具有相同性质的数据元素的集合
数据结构：相互之间存在一种或多种特定关系的数据元素的集合
包含逻辑结构、存储结构、数据的运算
Data Structure=(D,S) 数据元素有限集、数据关系有限集，注意对应

题1.以下说法正确的是()
A.数据项是数据的基本单位
B. 数据元素是数据的最小单位
C.数据结构是带结构的数据项的集合
D.数据元素可由若干数据项组成
答案：D
题2.数据的逻辑结构从形式上可用二元组(D,R)表示,其中R是()的有限集
A.算法
B.数据元素
C.数据项
D. 数据关系
答案：D

逻辑结构分为线性结构（线性表（栈、队列、串、数组）（一对多））、非线性结构（集合、树形结构（一对多）、图形结构或网状结构（多对多））

存储结构（物理结构）：顺序存储（逻辑上和物理上位置一致）、链式存储（借助指示元素存储地址的指针）、索引存储（索引表：索引项（关键字、地址））、散列存储（哈希存储）（关键字通过散列函数到存储地址）

2.算法

有穷性（有穷步骤和时间）、确定性、可行性、输入、输出

目标：正确性、可读性、健壮性、效率与低存储量需求

时间复杂度只保留频度之和的数量级

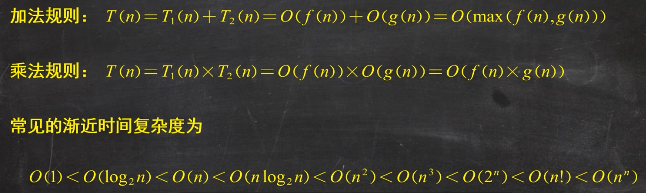
3.顺序表

①线性表：具有相同数据类型的n个数据元素的有限序列
直接前驱/直接后继

特点

实训代码

题目：

本关任务：对于顺序存储的线性表完成两个操作函数，分别实现顺序表中数据的插入、删除功能。
相关知识
实训中的类型定义及子函数的作用如下： 
（1）定义顺序表类型SqList; 
#define MAXSIZE 100 //顺序表可能达到的最大长度 
typedef int ElemType; //假设顺序表中所有元素为int类型 
typedef struct { 
	ElemType *elem; //指向数据元素的基地址 
	int length; //顺序表的当前长度 
} SqList;
（2）子函数InitList(SqList &L)，实现顺序表的初始化; 
（3）子函数CreateList(SqList &L)，实现顺序表的创建，从键盘上依次输入整型数据元素，创建顺序表; 
（4）子函数ListInsert(SqList &L,int i ,ElemType e)，实现顺序表中的插入运算; 
（5）子函数 ListDelete(SqList &L,int i)，实现顺序表中的删除运算; 
（6）子函数PrintList(SqList L)，实现顺序表的打印输出。

答案：

#include <iostream>
using namespace std;
#define MAXSIZE 100
typedef int ElemType;           //假设顺序表中所有元素为int类型
typedef struct
{   ElemType *elem;     //存放顺序表的元素
    int length;                 //顺序表的实际长度
} SqList;                       //顺序表类型
  
void InitList(SqList &L)           //由于L要回传给值参，所以用引用类型
{  L.elem = new ElemType[MAXSIZE];   //为顺序表分配空间
    if(!L.elem) exit(-2);       //存储分配失败
    L.length=0;            //空表长度为0
}
void CreateList(SqList &L)  //创建顺序表
{
    int i,n;
    cin>>n;
    for(i=0;i<n;i++)
    { cin>>L.elem[i];}
    L.length=n;
}
  
int ListInsert(SqList &L,int i,ElemType e)
{//在顺序表L中第i个位置插入新元素e。
//请在这里补充代码，完成顺序表的插入操作。  
    if(i<1 or i>L.length+1)return 0;
    for(int j=L.length-1;j>=i-1;j--){
        L.elem[j+1]=L.elem[j];
    }
    L.elem[i-1]=e;
    ++L.length;
    return 1;
}
int ListDelete(SqList &L,int i)
{//在顺序表L中删除第i个元素e。
//请在这里补充代码，完成顺序表的删除操作。  
    if(i<1 or i>L.length+1)return 0;
    for(int j=i-1;j<L.length;j++){
        L.elem[j]=L.elem[j+1];
    }
    --L.length;
    return 1;
}
void PrintList(SqList L)
{   int i;
    for (i=0;i<L.length;i++)
        cout<<L.elem[i]<<" ";
    cout<<endl;
}
int main()
{   int r,k;
    SqList L;
    InitList(L);//初始化顺序表L
    CreateList(L);
    r=ListInsert(L,5,6);    
    if(r)
        PrintList(L);
    else
        cout<<"插入位置非法"<<endl;
    k=ListDelete(L,3);
    if(k)
        PrintList(L);
    else
        cout<<"删除位置非法"<<endl;
    return 0;}

题目2

本关任务：对于无序的顺序表，可能存在着一些值相同的“多余”数据元素（类型为整型），编写一个程序将“多余”的数据元素从顺序表中删除，使该表由一个“非纯表”（值相同的元素在表中可能有多个）变成一个“纯表”（值相同的元素在表中只保留第一个）。

答案：

#include <iostream>
using namespace std;
#define MAXSIZE 100
typedef int ElemType;           //假设顺序表中所有元素为int类型
typedef struct
{   ElemType *elem;     //存放顺序表的元素
    int length;                 //顺序表的实际长度
} SqList;                       //顺序表类型
  
void InitList(SqList &L)          //由于L要回传给值参，所以用引用类型
{  L.elem = new ElemType[MAXSIZE];   //为顺序表分配空间
    if(!L.elem) exit(-2);       //存储分配失败
    L.length=0;            //空表长度为0
}
void CreateList(SqList &L)  //创建顺序表
{
    int i,n;
    //cout<<"请输入元素个数"<<endl;
    cin>>n;
    //cout<<"请依次输入元素"<<endl;
    for(i=0;i<n;i++)
    { cin>>L.elem[i];}
    L.length=n;
}
  
//编写子函数，将“多余”的数据元素从顺序表中删除，值相同的元素在表中只保留第一个。
void DeleteList(SqList &L)
{
    int newlen=0;
    for(int i=0;i<L.length;i++)
    {
        bool ischongfu=false;
        for(int j=0;j<newlen;j++)
        {
            if(L.elem[i]==L.elem[j])
            {
                ischongfu=true;
                break;
            }
        }
        if(!ischongfu)
        {
            L.elem[newlen]=L.elem[i];
            newlen++;
        }
    }
    L.length=newlen;
}
  
void PrintList(SqList L)
{   int i;
    for (i=0;i<L.length;i++)
        cout<<L.elem[i]<<" ";
    cout<<endl;
}
int main()
{  
    SqList a;
    InitList(a);
    CreateList(a);
    DeleteList(a);
    PrintList(a);
//编写主函数，将去重后的顺序表输出。
}

4.链表

链式存储的线性表
每个都有data（数据）和next（后继结点地址）

typedef struct LNode{
Elemtype data;
struct LNode *next;
}LNode,*Linklist; //前者强调结点，后者强调链表

结构有带头结点和不带头结点的

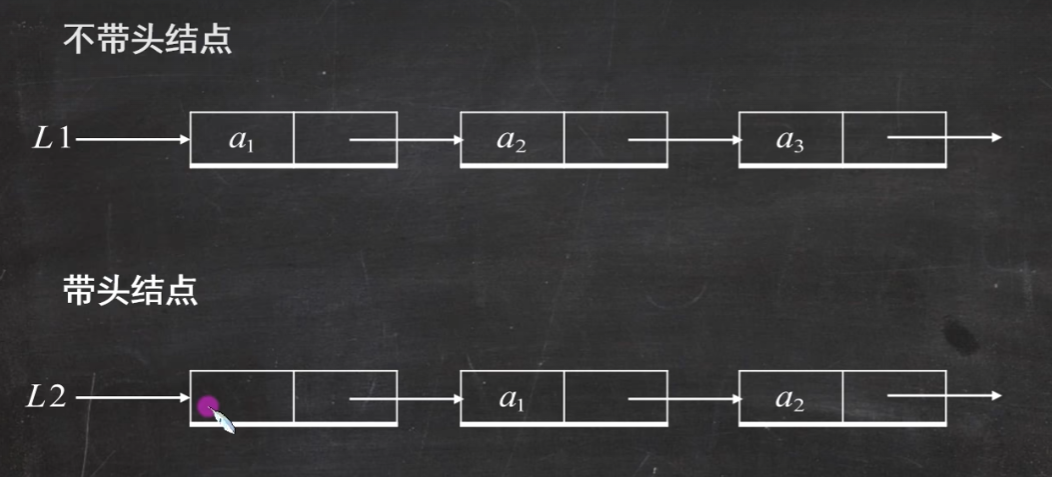
题1.若线性表采用链式存储,则表中各元素的存储地址
A. 必须是连续的
B. 部分地址是连续的
C. 一定是不连续的
D. 不一定是连续的
答案：D
题2.单链表中,增加一个头结点的目的是()
A. 使单链表至少有一个结点
B. 标识表结点中首结点的位置
C. 方便运算的实现
D. 说明单链表是线性表的链式存储
答案：C

单链表的实现

实训1代码

题目：

本关任务：对于链式存储的线性表完成三个操作函数，分别实现单链表的创建、数据的插入、删除功能。
实训中的类型定义及子函数的作用如下：
（1）定义单链表类型;
typedef struct LNode{
     ElemType   data;          //结点的数据域
     struct LNode  *next;   //结点的指针域
}LNode,*LinkList;
（2）子函数InitList(LinkList &L)，实现单链表的初始化;
（3）子函数CreateList(LinkList &L,int n)，实现单链表的创建;
（4）子函数ListInsert(LinkList &L,int i,ElemType e)，实现单链表中的插入运算;
（5）子函数 ListDelete(LinkList &L,int i,ElemType &e)，实现单链表中的删除运算;
（6）子函数PrintList(LinkList L)，实现单链表的打印输出。

答案：

#include<iostream>
using namespace std;
#define OK 1
#define ERROR 0
typedef int Status;
typedef int ElemType;
  
struct LNode
{
    ElemType data;
    struct LNode *next;
};
typedef struct LNode *LinkList; //定义LinkList类型
  
void InitList(LinkList &L)
{
    L=new LNode;
    L->next=NULL;
}
  
void CreateList(LinkList &L,int n)
{ //逆位序(插在表头)输入n个元素的值，建立带头结点的单链表L
    //请在这里补充代码，完成单链表的创建。
    L=new LNode;
    L->next=NULL;
    for(int i=n;i>0;--i)
    {
        LinkList p=new LNode;
        cin>>p->data;
        p->next=L->next;
        L->next=p;
    }
    /*第二种方法
    int x;
    LinkList p;
    for(int i=0;i<n;i++)
    {
        cin>>x;
        p=(LNode *)malloc(sizeof(p));
        p->data=x;
        p->next=L->next;
        L->next=p;
    }
    */
}
  
int ListInsert(LinkList &L,int i,ElemType e)
{ //在带头结点的单链表中第i个位置插入值为e的新结点
    //请在这里补充代码，完成单链表的插入。
    LinkList p=L;int j=0;
    while(p and j<i-1){p=p->next;++j;}
    if(!p or j>i-1)return 0;
    LinkList s=new LNode;
    s->data=e;
    s->next=p->next;
    p->next=s;
    return 1;
}
  
int ListDelete(LinkList &L,int i)
{ //在带头结点的单链表中，删除第i个结点
    //请在这里补充代码，完成单链表的删除。
    LinkList p=L;int j=0;
    while(p->next and j<i-1)
    {
        p=p->next;
        ++j;
    }
    if(!(p->next) or j>i-1)return 0;
    LinkList q=p->next;
    p->next=q->next;
    LinkList data,e;
    delete q;
    return 1;
}
  
void PrintList(LinkList &L)
{
    LinkList p=L->next;
    while(p)
    {
        cout<<p->data<<" ";
        p=p->next;
    }
    cout<<endl;
}

  
int main()
{
    int n,i,j,e,l;
    LinkList L;
    cin>>n;
    InitList(L);
    CreateList(L,n);
    PrintList(L);
    cin>>i;
    cin>>e;
    j=ListInsert(L,i,e);
    if(j)
        PrintList(L);
    else
        cout<<"插入位置非法";
    cin>>i;
    j=ListDelete(L,i);
    if(j)
        PrintList(L);
    else
        cout<<"删除位置非法"<<endl;
    return 0;
}

实训题目2

题目：

本关任务：编写一个程序，实现带头结点的单链表的逆置。
为了完成本关任务，你需要掌握：
1.单链表中头插法的实现过程，
2.单链表中指针的修改。

答案：

#include<iostream>
using namespace std;
#define OK 1
#define ERROR 0
typedef int Status;
typedef int ElemType;
  
struct LNode
{
    ElemType data;
    struct LNode *next;
};
typedef struct LNode *LinkList; //定义LinkList类型
  
void InitList(LinkList &L)
{
    L=new LNode;
    L->next=NULL;
}
  
void CreateList(LinkList &L,int n) //逆位序(插在表头)输入n个元素的值，建立带头结点的单表L
{
    int i;
    LinkList p;
    L=new LNode;
    L->next=NULL;
    //cout<<"请输入n个数据"<<endl;
    for(i=n;i>0;--i)
    {
        p=new LNode;
        cin>>p->data;
        p->next=L->next;
        L->next=p;
    }
}
  
//编写子函数，实现单链表的逆置
void ReverseList(LinkList &L)
{
    LinkList p;
    p=L->next;
    L->next=NULL;
    while(p)
    {
        LinkList q=p;
        p=p->next;
        q->next=L->next;
        L->next=q;
    }
}
  
void PrintList(LinkList &L)
{
    LinkList p=L->next;
    while(p)
    {
        cout<<p->data<<" ";
        p=p->next;
    }
    cout<<endl;
}
  

  
int main()
{//编写主函数，输出逆置后的单链表
    LinkList a;
    InitList(a);
    int n;
    cin>>n;
    CreateList(a,n);
    ReverseList(a);
    PrintList(a);
}

按序号查找结点值O(n)

LNode *GetElem (LinkList L,int i){
	int j=1;
	LNode *p = L-> next;
	if(i == 0)return L;
	if(i<0)return NULL;
	while (p&&j<i){
		p=p->next;j++;
	}
	return p;
}

按值查找表结点O(n)

LNode *LocateElem (LinkList L, ElemType e){
	LNode *p = L-> next;
	while (p != NULL&&p-> data != e)
		p=p->next;
	return p;
}

题1.从一个具有n个结点的单链表中查找其值等于x的结点时,在查找成功的情况下,需比较()个元素结点
A. n/2 B. n C.(n+1)/2 D.(n-1)/2
答案：C
解析：求的是平均比较次数，所以x在每一个位置都有可能
(1+2+...+n)/n=(n+1)/2

插入结点

先按位查找p=GetElem(L,i-1)
然后让插入的结点的后继结点为原来第i-1个结点的后继结点(s->next=p->next)

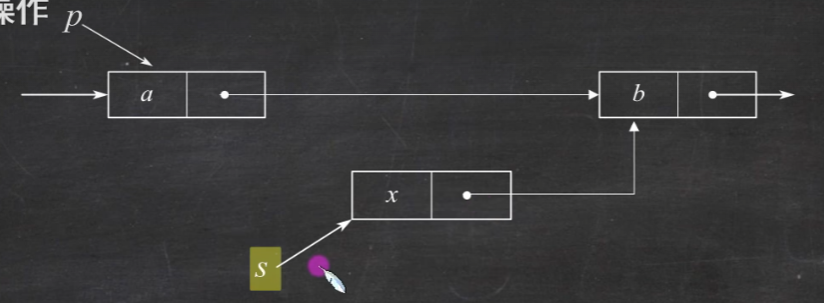
最后让p的后继结点变成s

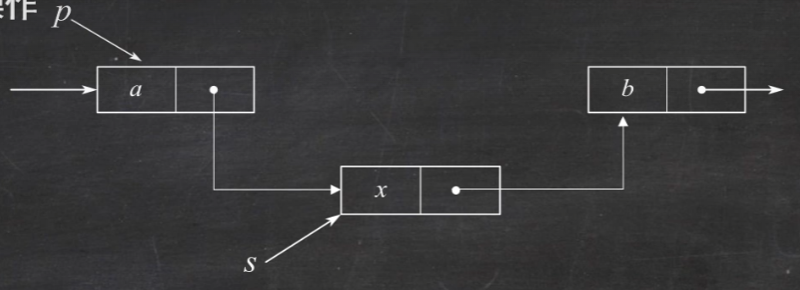
题2.在单链表中,已知p,q,s是指向结点的指针,且q是p的直接前驱,若在q和p之间插入s,则需执行()
A. s->next = p->next; p-> next= s;
B. q-> next =s; s-> next = p;
C. p->next=s-> next; s-> next = p;
D.p-> next=s; s-> next= q;
答案：B
解析：画个图体会一下

删除结点

先按位查找p=GetElem(L,i-1);
删除的结点q=p->next;

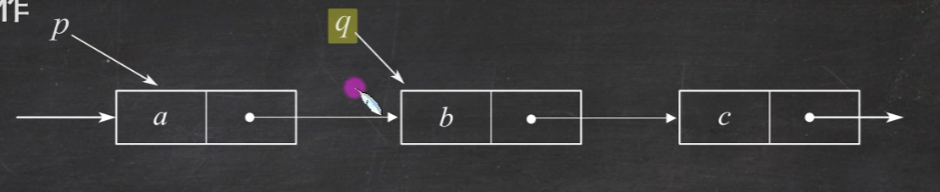
绕过区间p->next=q->next;

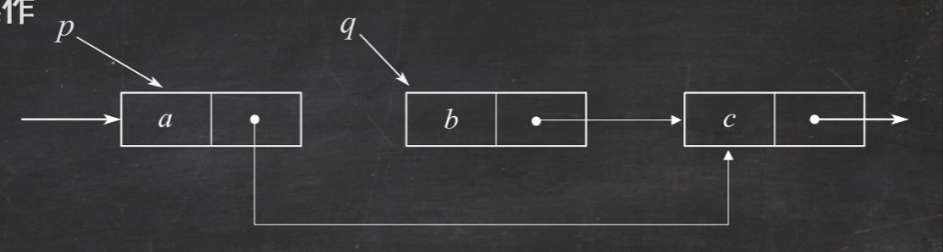
删除结点free(q);

循环单链表

L->next=L
循环链表中每一个元素都有后继
题4.在以下的叙述中,正确的是()
A. 线性表的顺序存储结构优于链式存储结构
B. 线性表的顺序存储结构适用于频繁插入或删除数据元素的情况
C. 线性表的链式存储结构适用于频繁插入或删除数据元素的情况
D. 线性表的链式存储结构优于顺序存储结构
答案：C

5.栈和队列

栈：先进后出
队列：先进先出
循环队列
初始时:Q.front =Q.rear=0
队首指针进1:Q.front=(Q.front +1)%MaxSize
队尾指针进 1:Q.rear= (Q.rear+1)%MaxSize
队列长度:(Q.rear - Q.front + MaxSize )%MaxSize
队空条件：Q.front==Q.rear
牺牲一个单元来区分队空和队满，入队时少用一个队列单元
队满条件：(Q.rear+1)%MAXSIZE==Q.front
没啥，直接看实训

实训

题目1：顺序栈的基本操作

本关任务：对于顺序存储的字符栈完成三个操作函数，分别实现顺序栈的初始化，数据的入栈和出栈功能。
相关知识
实训中的类型定义及子函数的作用如下：
（1）定义顺序栈类型SqStack;
typedef struct
{
 SElemType *base;
 SElemType *top;
 int stacksize;
}SqStack;
（2）子函数InitSqStack(SqStack &st)，实现顺序栈的初始化;
（3）子函数Push(SqStack &st, char e)，实现顺序栈中的入栈运算;
（4）子函数Pop(SqStack &st, char &e)，实现顺序栈中的出栈运算;
（5）主函数，在主函数中调用上述子函数，输出相应的结果。

答案：

#include <iostream>
using namespace std;
#define MAXSIZE 10
#define OVERFLOW -2
typedef char SElemType;
typedef struct
{
    SElemType *base;
    SElemType *top;
    int stacksize;
}SqStack;
void InitStack(SqStack &S)
{//请在这里补充代码，完成顺序栈的初始化。
    S.base=new SElemType[MAXSIZE];
    S.top=S.base;
    S.stacksize=MAXSIZE;
}
  
int Push(SqStack &S,SElemType e)
{//请在这里补充代码，完成顺序栈的入栈操作。
    if(S.top-S.base==S.stacksize)return 1;
    *S.top=e;
    S.top++;
    return 0;
}
  
int Pop(SqStack &S,SElemType &e)
{//请在这里补充代码，完成顺序栈的出栈操作。
    if(S.top==S.base)return 1;
    --S.top;
    e=*S.top;
    return 0;
}

int main()
{
    SqStack st;
    char e,a[MAXSIZE];int n;
    InitStack(st);
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>a[i];
    for(int j=0;j<n;j++)
        Push(st,a[j]);
    for(int k=0;st.top!=st.base;k++)
    {
        Pop(st,e);
        cout<<e<<" ";
    }
    return 0;
}

题目2：顺序队列的基本操作

题目：

本关任务：对于顺序存储的字符队列完成两个操作函数，分别实现顺序循环队列的的入队和出队功能。
相关知识
（1）定义循环队列类型SqQueue;
typedef struct
{
 QElemType *base;
 int front;
 int rear;
}SqQueue;
（2）子函数InitQueue(SqQueue &sq)，实现循环队列的初始化;
（3）子函数EnQueue(SqQueue &sq,char x)，实现循环队列中的入队运算;
（4）子函数DeQueue(SqQueue &sq,char &x)，实现循环队列中的出队运算;
（5）编写主函数，在主函数中调用上述子函数，输出相应的结果。

答案：

#include <iostream>
using namespace std;
#define MAXSIZE 10
#define OVERFLOW -2
typedef char QElemType;
typedef struct
{
    QElemType *base;
    int front;
    int rear;
}SqQueue;
  
void InitQueue(SqQueue &Q)
  
{
    Q.base=new QElemType[MAXSIZE];
    Q.front=Q.rear=0;
}
  
int EnQueue(SqQueue &Q,QElemType e)
{//请在这里补充代码，完成顺序队列的入队操作。
    if((Q.rear+1)%MAXSIZE==Q.front)return 1;
    Q.base[Q.rear]=e;
    Q.rear=(Q.rear+1)%MAXSIZE;
    return 0;
}
  
int DeQueue(SqQueue &Q,QElemType &e)
{//请在这里补充代码，完成顺序队列的出队操作。
    if(Q.front==Q.rear)return 1;
    e=Q.base[Q.front];
    Q.front=(Q.front+1)%MAXSIZE;
    return 0;
}
  
int main()
{//请在这里补充代码，验证队列的入队和出队操作。从键盘输入字符，进行入队。而后依次出队。
    SqQueue queues;
    InitQueue(queues);
    char a;
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>a;
        EnQueue(queues,a);
    }

    for(int i=0;i<n;i++)
    {
        DeQueue(queues,a);
        cout<<a<<" ";
    }
}

题目3：用栈实现进制转换

题目：

本关任务：编写一个程序，实现对于任意一个非负十进制数，打印输出与其等值的八进制数。

相关知识
算法基本思想：
当将一个十进制整数N转换为八进制数时，在计算过程中，把N与8求余得到的八进制数的各位依次进栈，计算完毕后将栈中的八进制数依次出栈输出，输出结果就是待求得的八进制数。
算法描述：
①初始化一个空栈S。
②当十进制数N非零时，循环执行以下操作：
●把N与8求余得到的八进制数压入栈S;
● N更新为N与8的商。
③当栈S非空时，循环执行以下操作：
●弹出栈顶元素e;
●输出e。

答案：

#include <iostream>
using namespace std;
#define MAXSIZE 10
#define OVERFLOW -2
typedef int SElemType;
typedef struct
{
    SElemType *base;
    SElemType *top;
    int stacksize;
}SqStack;
  
void InitStack(SqStack &S)
{//请在这里补充代码，完成顺序栈的初始化。
    S.base=new SElemType[MAXSIZE];
    S.top=S.base;
    S.stacksize=MAXSIZE;
}
  
int Push(SqStack &S,SElemType &e)
{
    if(S.top-S.base==S.stacksize)return OVERFLOW;
    *S.top=e;
    S.top++;
    return 0;
}
  
int Pop(SqStack &S,SElemType &e)
{
    if(S.top==S.base)return 1;
    --S.top;
    e=*S.top;
    return 0;
}
//编写一个子函数，实现对于任意一个非负十进制数，打印输出与其等值的八进制数
  
int main()
{
    SqStack stk;
    InitStack(stk);
    int n,e,s;
    cin>>n;
    while(n!=0)
    {
        s=n%8;
        Push(stk,s);
        n=n/8;
    }
    for(int i=0;stk.top!=stk.base;i++)
    {
        Pop(stk,e);
        cout<<e;
    }
    //补充完整主函数

}

题1.向顺序栈中压入新元素,应当()
A.先移动栈顶指针,再存入元素
B. 先存入元素,再移动栈顶指针
C.先后次序无关紧要
D. 同时进行
答案：A
题2.链栈对比顺序栈主要优点在于()
A.通常不会出现栈满的情况
B. 通常不会出现栈空的情况
C. 插入操作更加方便
D. 删除操作更加方便
答案：A
解析：链栈的优点是便于多个栈共享存储空间和提高其效率,且不存在栈满上溢的情况
题2.将一个递归算法改为对应的非递归算法时,通常需要使用()
A.栈
B.队列
C.循环队列
D.优先队列
答案：A
解析：栈能适用于递归算法,表达式求值以及括号匹配等问题

6.树、二叉树

树：n个结点的有限集
每个数据元素只可能有一个直接前驱但是可以有多个直接后继
祖先、双亲、孩子
结点的度：该结点的孩子个数
树的度：树中结点的最大度数
分支结点（非终端结点）度大于0
叶子结点（终端结点）度等于0
兄弟结点：具有相同双亲的结点
深度：根结点从叶子结点向下
高度：叶子结点到根结点向上
有序树：从左到右有次序
无序树：从左到右无次序
路径：两个结点之间经过的结点序列
路径长度：路径上经过的边的条数

树的性质：

1、树中结点树等于所有结点的度数+1
2、度为m的树中第i层上至多有m^(i-1)个结点
题2.对一棵n个结点的树,则该树中结点的度数之和为()
A. n
B. n-1
C.n+1
D. 不确定
答案：B

题3.设一棵度为3的树中有2个度数为1的结点,2个度数为2的结点,2个度数为3
的结点,则该树中有()个度数为0的结点
A. 5
B. 6
C. 7
D. 8
答案：C
解析：设树中有x个度数为0的结点
2+2+2+x=2×1+2×2+2×3

二叉树

满二叉树：二叉树结点都是满的
完全二叉树：叶子结点不一定是满的，但是后继都是2个

性质1：非空二叉树上的叶子结点数等于度为2的结点数加1,即n0=n2+1
题1.一棵二叉树有67个结点,这些结点的度要么是0,要么是2。这棵二叉树中二叉树中度为2的结点有（）个
n0+n2=67 -> n2+n2+1=67

题2.将一棵有100个结点的完全二叉树,从根这一层开始,每一层从左到右依次
对结点编号,根结点的编号为1,则编号为49的结点的双亲编号为()
A. 23
B. 25
C. 24
D.无法确定
答案：C
解析：49/2取整

二叉树存储结构

（1）顺序存储结构：指用一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树的结点元素,即将完全二叉树上编号为i的结点元素存储在一维数组下标i-1的分量中

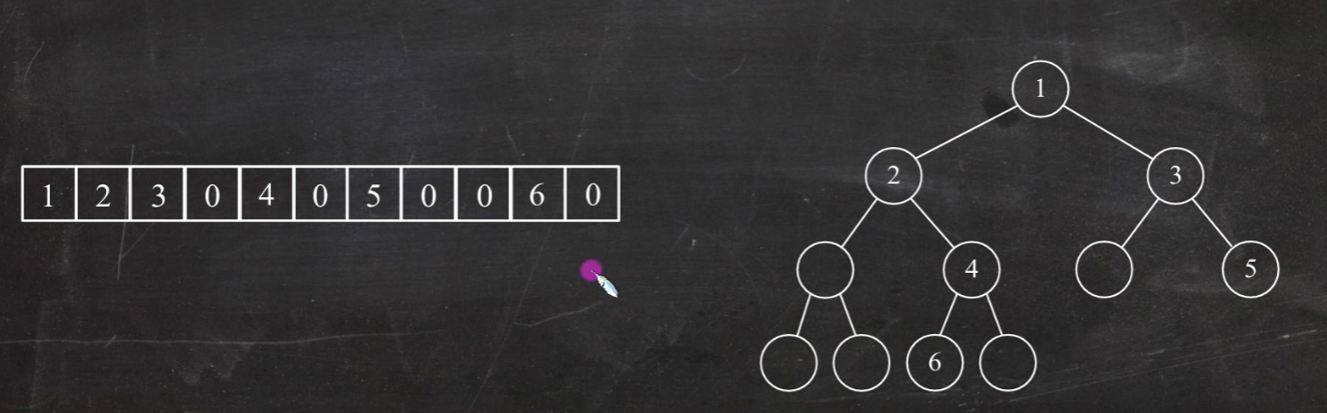
（2）链式存储结构：用链表结点来存储二叉树中的每个结点
每个结点：lchild（左孩子地址）、data（数据）、rchild（右孩子地址）

typedef struct BiTNode {
ElemType data;
struct BiTNode *Ichild, *rchild;
} BiTNode, *BiTree;

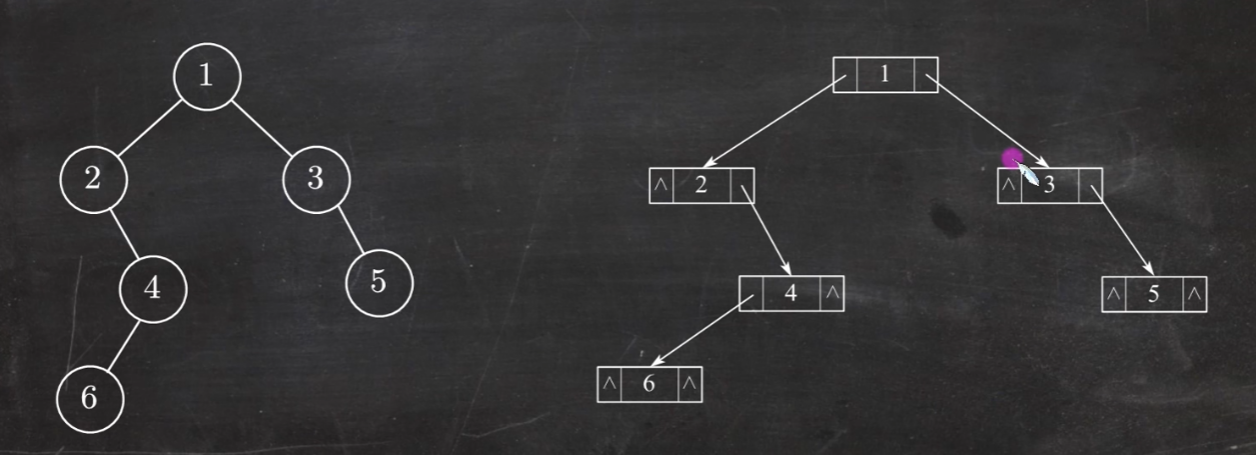
在含有n个结点的二叉链表中,含有n+1个空链域,含有n-1个非空链域

二叉树的遍历

原则：先左子树再右子树
先序遍历：根、左、右

void PreOrder(BiTree T) {
	if (T != NULL) {
		visit(T);
		PreOrder(T->Ichild);
		PreOrder(T->rchild) ;
	}
}

中序遍历：左、根、右

void InOrder (BiTree T) {
	if (T != NULL) {
		InOrder (T->Ichild) ;
		visit(T);
		InOrder (T->rchild) ;
	}
}

后序遍历：右、根、左

void PostOrder (BiTree T) {
	if (T != NULL) {
		PostOrder (T->Ichild);
		PostOrder (T->rchild) ;
		visit(T);
	}
}

层次遍历——队列

void LevelOrder (BiTree T) {
	InitQueue (Q) ;
	BiTNode *p=T;
	EnQueue (Q, p) ;
	while (!IsEmpty (Q)) {
		DeQueue (Q, p) ;
		visit(p);
		if (p->Ichild != NULL)
			EnQueue (Q, p->Ichild);
		if (p->rchild != NULL)
			EnQueue(Q,p->rchild);
	}
}

题1.已知一棵二叉树的先序遍历结果为ABCDEF,中序遍历结果为 CBAEDF,
则后序遍历的结果为()
A. CBEFDA
B. FEDCBA
C. CBEDFA
D. 不定
答案：A
解析：根据逻辑判断

找根结点：后序根结点一定是最后访问的，先序的根结点一定是第一个访问的

题2.某二叉树结点的中序序列为:ABCDEFG,后序序列为:BDCAFGE,则其根结点
左子树中结点数目为()
A. 3
B. 2
C. 4
D. 5

实训

题目1

本关任务：编写一个程序，先由先序遍历序列建立一棵二叉树，再分别实现二叉树先序、中序、后序遍历的递归算法，最后利用后序遍历方法实现求解二叉树深度的操作。

相关知识
为了完成本关任务，你需要掌握：1.如何由先序遍历序列建立一棵二叉树，2.如何使用递归算法实现遍历。

由先序遍历序列建立一棵二叉树

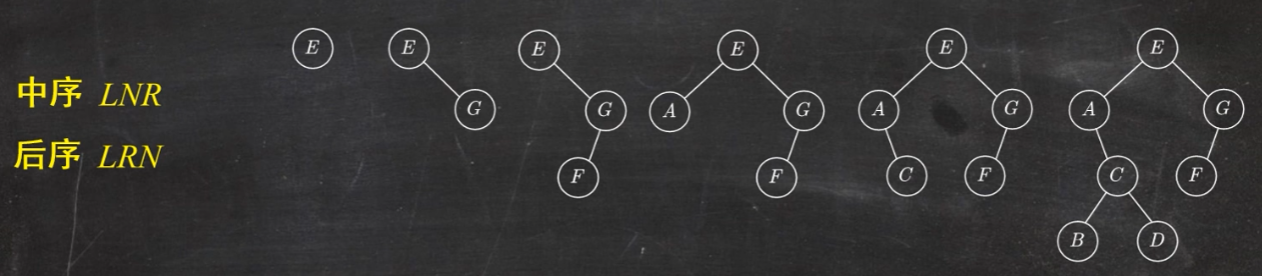
如图所示二叉树，输入先序序列为：
ABC##DE#G##F###
采用以下函数实现二叉树的二叉链表结构创建
void CreateBiTree(BiTree &T)
{
    char ch;
    cin >> ch;
    if(ch=='#')  T=NULL;            //递归结束，建空树
    else{
        T=new BiTNode;
        T->data=ch;                    //生成根结点
        CreateBiTree(T->lchild);    //递归创建左子树
        CreateBiTree(T->rchild);    //递归创建右子树
    }
}    

答案

#include<iostream>
using namespace std;
  
//二叉树的二叉链表存储表示
typedef struct BiNode
{              
    char data;                  //结点数据域
    struct BiNode *lchild,*rchild;  //左右孩子指针
}BiTNode,*BiTree;
  
void CreateBiTree(BiTree &T)
{
    char ch;
    cin >> ch;
    if(ch=='#')  T=NULL;            //递归结束，建空树
    else{
        T=new BiTNode;
        T->data=ch;                    //生成根结点
        CreateBiTree(T->lchild);    //递归创建左子树
        CreateBiTree(T->rchild);    //递归创建右子树
    }
}    
  
void PreOrderTraverse(BiTree T)
{  
    //先xu遍历二叉树T的递归算法

    if(T)
    {
        cout<<T->data;
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);
    }
}

  
void InOrderTraverse(BiTree T)
{  
    //中序遍历二叉树T的递归算法
    if(T)
    {
        InOrderTraverse(T->lchild);
        cout<<T->data;
        InOrderTraverse(T->rchild);
    }
}
  
void postOrderTraverse(BiTree T)
{  
    //后序遍历二叉树T的递归算法
    if(T)
    {
        postOrderTraverse(T->lchild);
        postOrderTraverse(T->rchild);
        cout<<T->data;
    }
}
  
int Depth(BiTree T)
{  
    int dep1=0,dep2=0;
    //通过后序遍历方式对二叉树T进行遍历，在遍历过程中计算二叉树的深度。
    if(T)
    {
        dep1=Depth(T->lchild);
        dep2=Depth(T->rchild);
        if(dep1>dep2)return (dep1+1);
        else return (dep2+1);
    }
    else return 0;
}
int main()
{
    BiTree tree;
    CreateBiTree(tree);
    cout<<"先序序列：";
    PreOrderTraverse(tree);
    cout<<endl;
    cout<<"中序序列：";
    InOrderTraverse(tree);
    cout<<endl;
    cout<<"后序序列：";
    postOrderTraverse(tree);
    cout<<endl;
    cout<<"二叉树的深度：";
    cout<<Depth(tree);
    return 0;
}

题目2

本关任务：编写一个程序，实现用二叉树表示算术表达式，通过对二叉树的遍历，中缀表达式的输出。

相关知识
为了完成本关任务，你需要掌握：1.如何用二叉树表示算术表达式，2.如何正确输出中缀表达式。

用二叉树表示算术表达式

一个算术表达式可以用二叉树表示，这个二叉树有2个特点：
1.叶子结点一定是操作数
2.分支结点一定是运算符
一棵二叉树可以转换为等价的中缀表达式，并且为了反映运算符的计算次序应该适当加上括号。
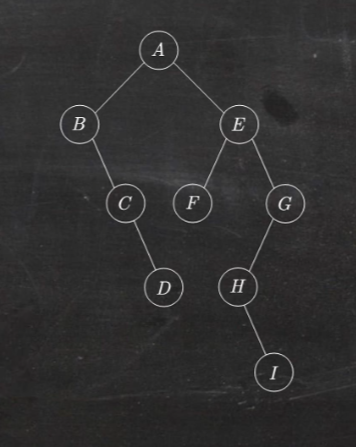
如图所示二叉树转换为等价的中缀表达式为：
a + b * (c – d) – e / f

输出中缀表达式
一个算术表达式可以用二叉树表示，这个二叉树的中序遍历序列加上必要的括号即为中缀表达式，在中序遍历二叉树的过程中，如果当前访问的是叶子结点，则无需加括号，可以直接输出。如果当前访问的结点深度大于1，则对左子树递归调用之前要加上左括号，对右子树递归调用之后要加上右括号。
算法基本思想：
输入：二叉链表根指针T，二叉树的深度deep
输出：中缀表达式
1.若指针T为空，则算法结束；
2.否则执行下述操作：
2.1 若deep>1，则输出左括号；
2.2 deep++；递归调用左子树；
2.3 输出T->data;
2.4 deep++；递归转换右子树；
2.5 若deep>1，则输出右括号；

答案

#include<iostream>
using namespace std;
  
//二叉树的二叉链表存储表示
typedef struct BiNode
{              
    char data;                      //结点数据域
    struct BiNode *lchild,*rchild;  //左右孩子指针
}BiTNode,*BiTree;
  
void CreateBiTree(BiTree &T)
{
    char ch;
    cin >> ch;
    if(ch=='#')  T=NULL;            //递归结束，建空树
    else{
        T=new BiTNode;
        T->data=ch;                    //生成根结点
        CreateBiTree(T->lchild);    //递归创建左子树
        CreateBiTree(T->rchild);    //递归创建右子树
    }
}    
  
void InExpression(BiTree T, int depth = 1) {
    if(T)
    {
        if((T->lchild or T->rchild) and depth>1)cout<<"(";//非叶子节点且深度大于1
        InExpression(T->lchild,depth+1);
        cout<<T->data;
        InExpression(T->rchild,depth+1);
        if((T->lchild or T->rchild) and depth>1)cout<<")";//非叶子节点且深度大于1
    }
}

  
int main()
{
    BiTree tree;
    CreateBiTree(tree);
    cout << "中缀表达式结果：";
    InExpression(tree);
    cout << endl;
    return 0;
}

树和森林

树的存储结构：双亲表示法、孩子表示法、孩子兄弟表示法
森林：多棵树的一个集合

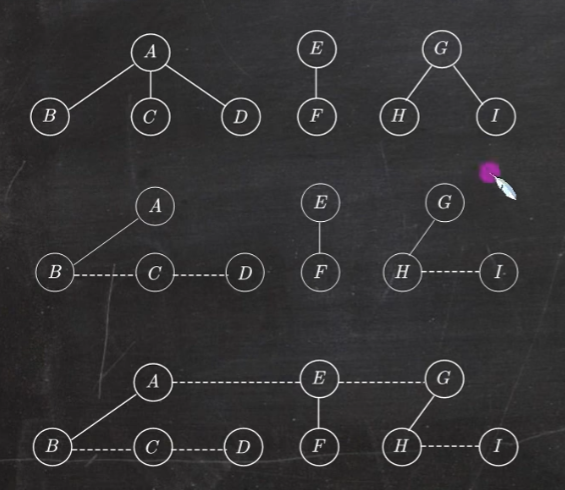
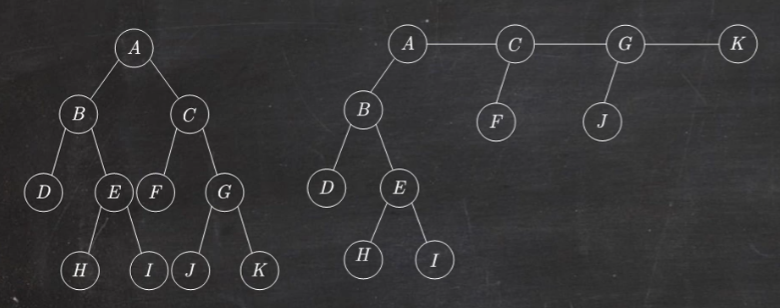
森林转换成二叉树的画法:（左孩子右兄弟）
(1)将森林中的每棵树转换成相应的二叉树
(2)每棵树的根也可视为兄弟结点，在每棵树之间加一根连线
(3)以第一棵树的根为轴心顺时针旋转 45°


题4.设森林F中有三棵树,第一、第二、第三棵树上的结点个数分别为M1,M2,M3
则与森林F对应的二叉树根结点的右子树上的结点个数为（）
A. M1
B. M1 + M2
C. M3
D. M2+ M3
答案：D

二叉树转化为森林就是反过来做上面的三个步骤

哈夫曼树

权：树中结点常被赋予一个代表某种意义的数值
结点带权路径长度：从树的根到任意结点的路径长度与该结点上权值的乘积
树的带权路径长度：树中所有叶结点的带权路径长度之和，记作$WPL = \sum_{i = 1}^{n} w_i l_i$（自己的数字乘线段个数）
哈夫曼树（最优二叉树）：树的带权路径长度最小的二叉树
构造哈夫曼树的步骤:
(1)将所有结点分别作为仅含一个结点的二叉树
(2)构造一个新结点,从中选取两棵根结点权值最小的树作为新结点的左、右子树,并且将新结点的权
值置为左、右子树上根结点的权值之和
(3)从中删除刚才选出的两棵树,同时将新得到的树加入森林中
(4)重复步骤(2)和(3),直至剩下一棵树为止

题1.有一电文使用五种字符a,b,c,d,e,其出现频率依次为4,7,5,2,9
(1)试画出对应的哈夫曼树(要求左子树根结点的权小于等于右子树根结点的权)
(2)求出每个字符的哈夫曼编码
(3)译出编码序列11000111000101011 的相应电文
(4)求带权路径长度

7.图

有向图：每条边都有方向<v,w>这个表示v到w的一条有向边
无向图：每条边都没方向(v,w)表示一条无向边
完全图：对于无向图，任意两个顶点都存在边n(n-1)/2；对于有向图，任意两个顶点之间都存在方向相反的两条弧n(n-1)
子图：图是子集

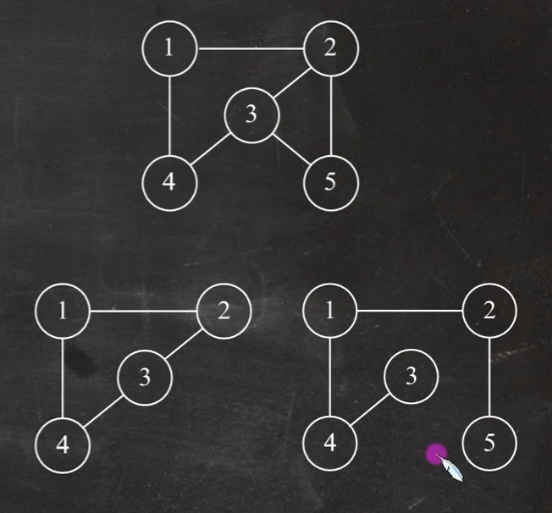
连通：两个点之间有路径连接就是连通的
连通图：图中任意两个顶点都是连通的
左边是非连通图，右边是连通图

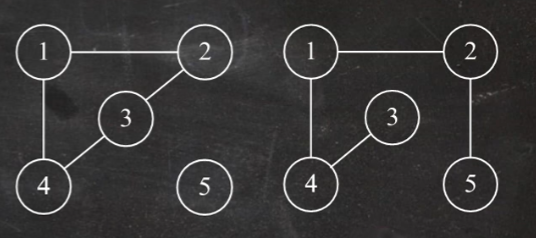
顶点的度

无向图：一个顶点有几条线就有多少度，无向图的全部顶点的度的和等于边数的两倍
对于有向图有入度和出度，入度是以顶点v为终点的有向边的数目，出度就是以顶点v为起点的有向边的数目
顶点的度等于入度和出度之和，有向图的全部顶点入度之和和出度之和相等，并且等于边数

边的权和网

每条边加入数值，相当于就是权值，有权值就叫带权图/网

路径、回路

回路：可以兜圈的

图的存储结构

邻接矩阵法
1,1不存在 1,2存在 1,3不存在 1,4存在 1,5不存在 依次类推

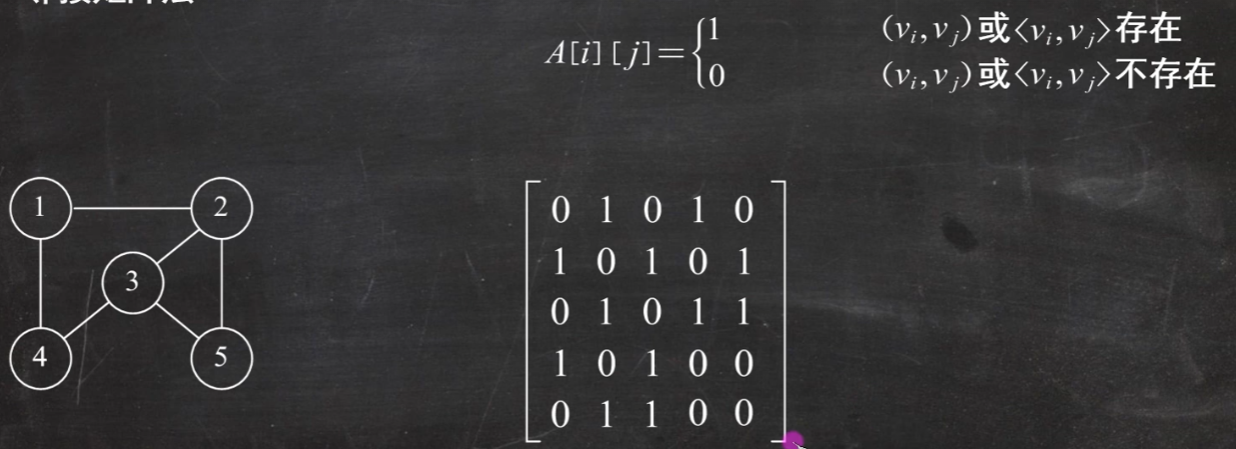
有向图注意加了方向，方向不对不算连接

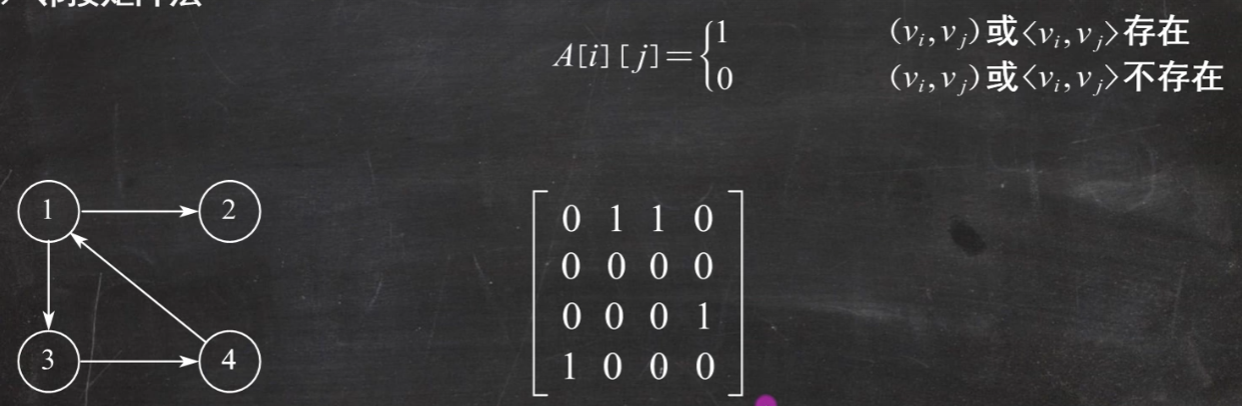
带权图表示方式不一样

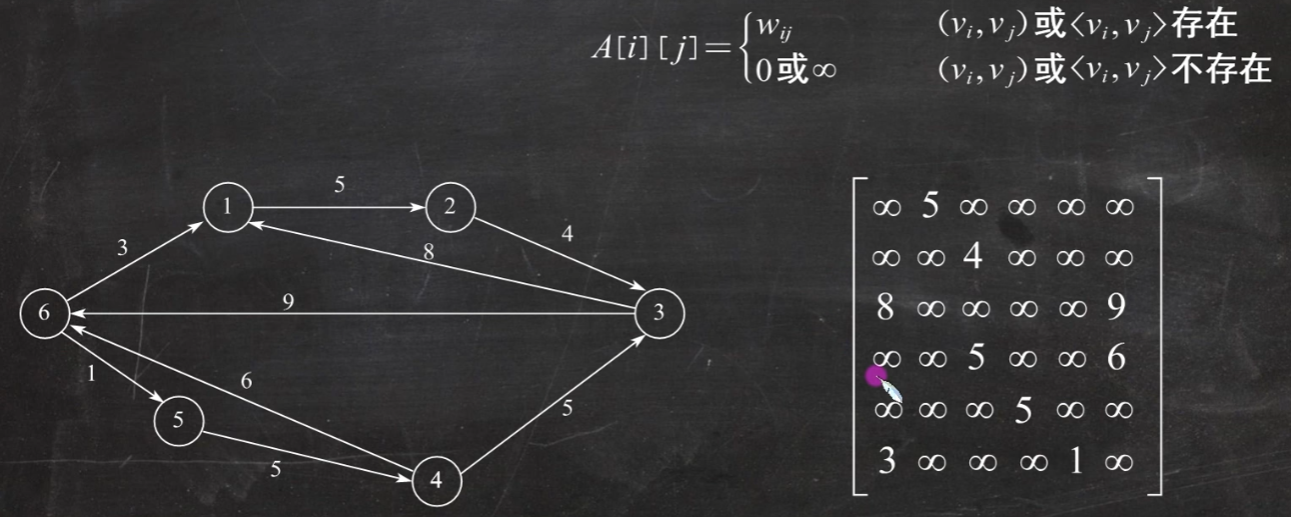
使用邻接矩阵存储方法:
n个顶点需要n个单元存储顶点信息,n^2个单元存储边(弧)。
优点:
容易实现图的操作,如:求某顶点的度、判断顶点之间是否有边(弧)、找顶点的邻接点等等。
缺点:
边或弧很少的稀疏图,仍需n+n2个存储空间,造成空间浪费。

题1. n个顶点的无向连通图用邻接矩阵表示时,该矩阵至少有（）个非零元素
答案：2(n-1)
题2.带权有向图G用邻接矩阵A存储,则顶点i的入度等于A中（）
A. 第i行非无穷元素之和
B. 第i列非无穷元素之和
C. 第i行非零非无穷元素之和
D. 第i列非零非无穷元素之和
答案：D
题3.用邻接矩阵存储一个图时,在不考虑压缩存储的情况下,所占用的存储空间大小只与图中顶点的个数有关,而与图的边数无关（）
答案：对

邻接表法
顶点表结点：顶点域、边表头指针
存边结点：邻接点域、指针域
表里的顺序可以随意调换（比如2，无论是1534还是1345都行，只要表示出一个结点连了多少条边）


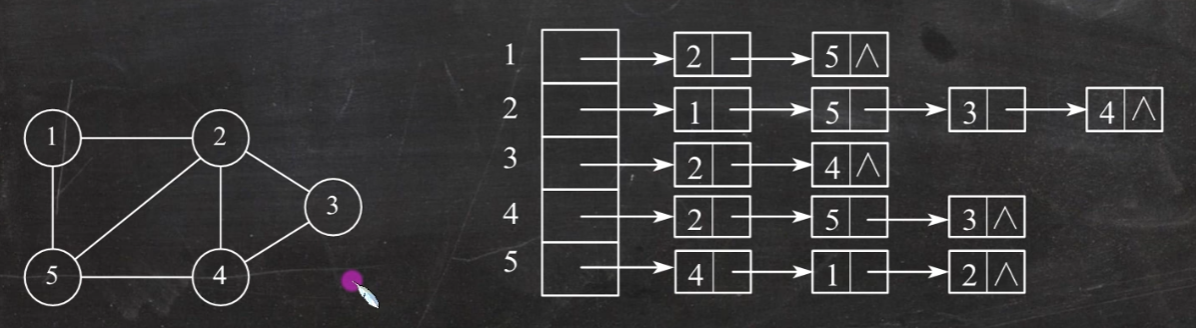
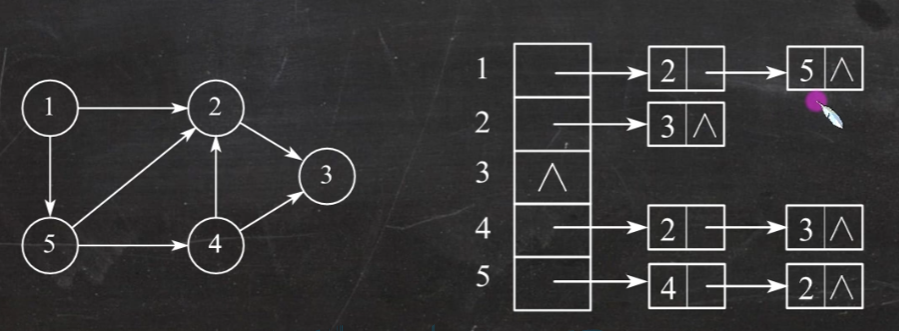
使用邻接表存储方法:
对于n个顶点,e条边的图:
无向图的邻接表需要n个头结点,2e个边结点。
有向图的邻接表需要n个头结点,e个边结点。

优点:
空间效率高;容易寻找顶点的邻接点;
缺点:
判断两顶点间是否有边或弧,需搜索两结点对应的单链表,没有邻接矩阵方便。

若G为无向图,则所需的存储空间为O(|V|+2|E|)
若G为有向图,则所需的存储空间为O(|V|+|E|)

题5.在有向图的邻接表表示中,下面()最费时间
A. 求某顶点的出度
B. 求某顶点的入度
C. 求图中顶点的个数
D. 求从某顶点出发的弧
答案：B

图的遍历

图的遍历:从图中的某一顶点出发,按照某种搜索方法沿着图中的所有顶点访问一次且仅访问一次
图的遍历算法主要有两种:广度优先搜索和深度优先搜索

（1）广度优先搜索（bfs）

类似于二叉树的层序遍历算法

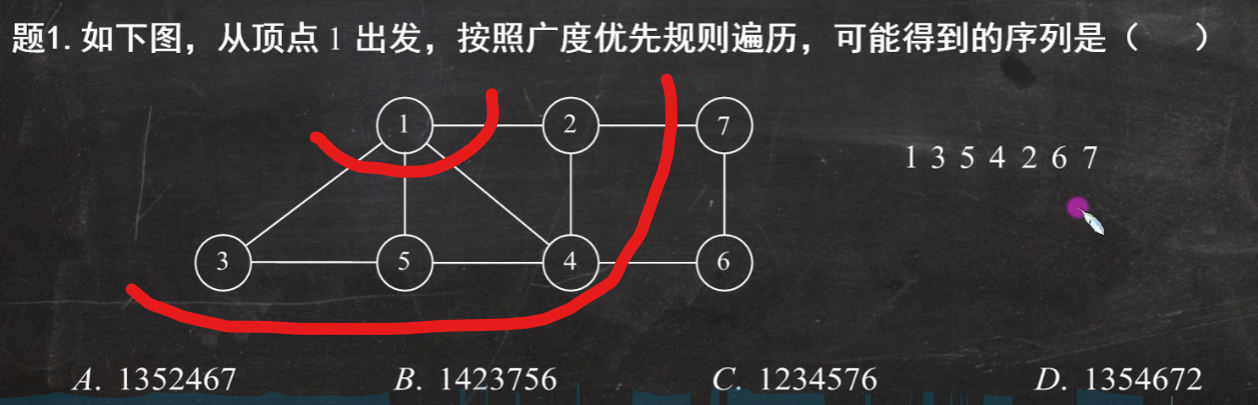
注意这里的顺序
先是1与2345相邻（12345）
然后再判断2与7相邻
然后3无
4与6相邻
所以选C

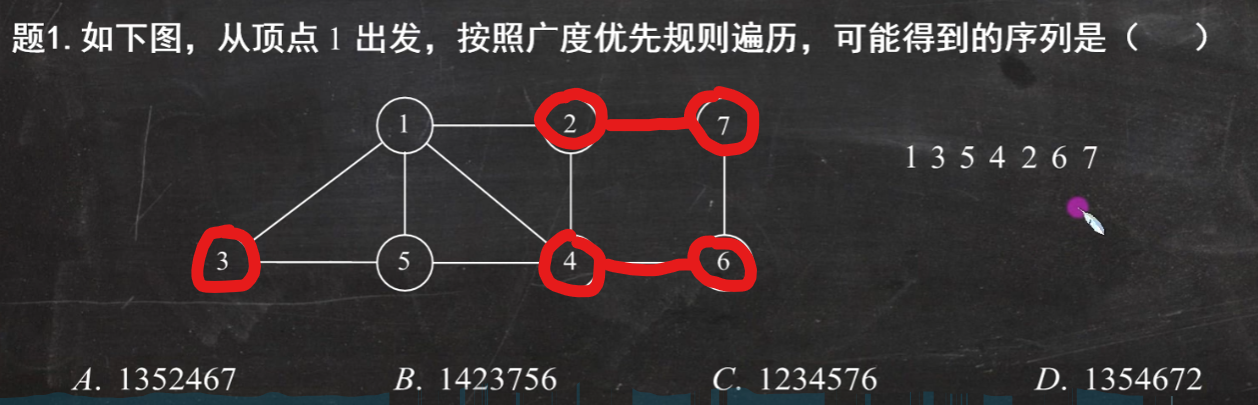
（2）深度优先搜索（dfs）

类似于树的先序遍历
题2.深度优先搜索遍历类似于树的（先序）遍历,广度优先搜索遍历类似于树的（层次）遍历，它们可以用（栈、队列）两种数据结构来实现。
题3. 若无向图 G 中的边的集合E={(a,b),(a,e),(a,c),(b,e),(e,d),(d,f),(f,c)},则
从顶点a出发进行深度优先遍历,可以得到的一种顶点序列为()
A. aedfcb
B. acfebd
C. aebcfd
D. aedfbc
注意：下一个点任意，找不到未访问点就返回上一步（回溯），直到遍历完为止
答案：A

图的应用

最小生成树

带权连通无向图中所有生成树中权值最小的生成树

Prim算法:

1、任取一顶点,去掉所有边
2、选择一个与当前顶点集合距离最近（权值最小）的顶点,并将该顶点和相应的边加入进来,同时不能形成回路
3、重复2,直至图中所有顶点都并入

Kruskal 算法:

1、去掉所有边
2、选边(权最小,且不构成回路)
3、重复2,直至图中所有顶点都并入

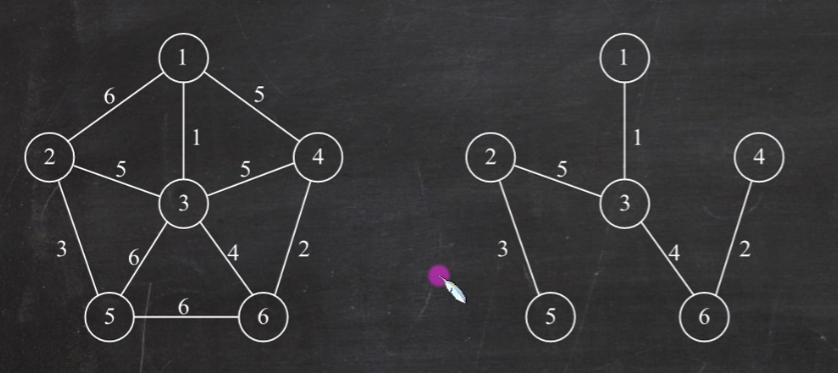
Prim：(1,3),(3,6),(6,4),(3,2),(2,5)
Kruskal：(1,3),(4,6),(2,5),(3,6),(2,3)

最短路径

dijkstra算法
d(u,u)=0
当u和v不相邻时d(u,v)=+无穷
先求v1，因为是起点，所以不管，加入表
然后接着填表

发现3最小，所以最短路径是v2，把v2加入表中，不需要计算后续步骤
第三步从v1到v2到v3权值是5，比7要小，所以加入表格
v1到v2到v5为9，比正无穷小，加入

这里选v3加入
每次下一步都是上一步的最小值相加

拓扑排序

AOV网:顶点表示活动<Vi,Vj>
拓扑排序：
1、每个顶点出现且只出现一次
2、若存在一条从顶点A到顶点B的路径,则在排序中顶点B出现在顶点A的后面
拓扑排序的算法的步骤:
1从AOV网中选择一个没有前驱的顶点并输出
2从网中删除该顶点和所有以它为起点的有向边
3重复1和2直到当前的AOV网为空或当前网中不存在无前驱的顶点为止

8.查找

（1）查找 在数据集合中，寻找满足某种条件的数据元素的过程
（2）查找表（查找结构） 用于查找的数据集合
（3）关键字 数据元素中某个数据项的值，用它可以标识一个数据元素 - 主关键字：关键字可以唯一地标识一个记录
（4）平均查找长度 所有查找过程中进行关键字的比较次数的平均值 $ASL = \sum_{i = 1}^{n} P_i C_i$

顺序查找

从头开始一个一个找，找到就返回，没找到就返回失败
题1.采用顺序查找方法查找长度为n的顺序表时,查找成功的平均查找长度为()
A. n
B. n/2
C. (n+1)/2
D. (n-1)/2
答案：C
拓展：不成功平均是n+1

实训

题目：

本关任务：编写程序，实现顺序表上的顺序查找。
相关知识
实训中的类型定义及子函数的作用如下：
（1）定义顺序表中数据元素类型;
typedef int ElemType;
typedef int KeyType;
typedef struct
{ KeyType key;    //存放关键字
  ElemType data;    //其他数据
} SqType;
（2）子函数Create_SSTable(SqType R[]) ，实现查找表的创建，从键盘上依次输入整型数据元素，创建查找表;
（3）子函数SqSearch(SqType R[],int n,KeyType k)，实现顺序查找;
（4）子函数Show_End(int result,int testkey)，输出查找的结果；
（5）主函数，在主函数中调用上述子函数，输出相应的结果。

答案：

#include<iostream>
using namespace std;
#define MAXSIZE 8
#define OK 1;
typedef int ElemType;
typedef int KeyType;
typedef struct
{ KeyType key;  //存放关键字
    ElemType data;  //其他数据
} SqType;
  
int Create_SSTable(SqType R[])
{
    for(int i=0;i<MAXSIZE;i++)  
    { cin>>R[i].key;}
    return 1;
}
  
int SqSearch(SqType R[],int n,KeyType k)
{  //请在这里补充代码，完成顺序查找。
    for(int i=0;i<MAXSIZE;i++)
    {
        if(R[i].key==k)return i+1;
    }
    return 0;
}

  
void Show_End(int result,int testkey)
{
    if(result==0)
        cout<<"未找到"<<testkey<<endl;
    else
        cout<<"找到"<<testkey<<"位置为"<<result<<endl;
}
  
int main()
{
    SqType R[MAXSIZE];
    Create_SSTable(R);
    int n=sizeof(R)/sizeof(R[0]);
    int testkey1,testkey2,result;
    cin>>testkey1;
    result=SqSearch(R,n,testkey1);
    Show_End(result,testkey1);
    cin>>testkey2;
    result=SqSearch(R,n,testkey2);
    Show_End(result,testkey2);
    return 0;
}

折半查找（二分查找）

仅适用于有序的顺序表
先给数据排序(例如按升序排好),形成有序表。
取中间记录R[mid].key与给定值key作比较,
若R[mid].key == key,则查找成功,返回mid;
若key<R[mid].key,则在中间记录的前半区继续查找;
若key>R[mid].key,则在中间记录的后半区继续查找。
重复上述过程,直到查找成功,或表中无此记录,查找失败。
是不是很像高中学的二分法hhh
注意：填空题大家可以转成树做更简单（二叉排序树）

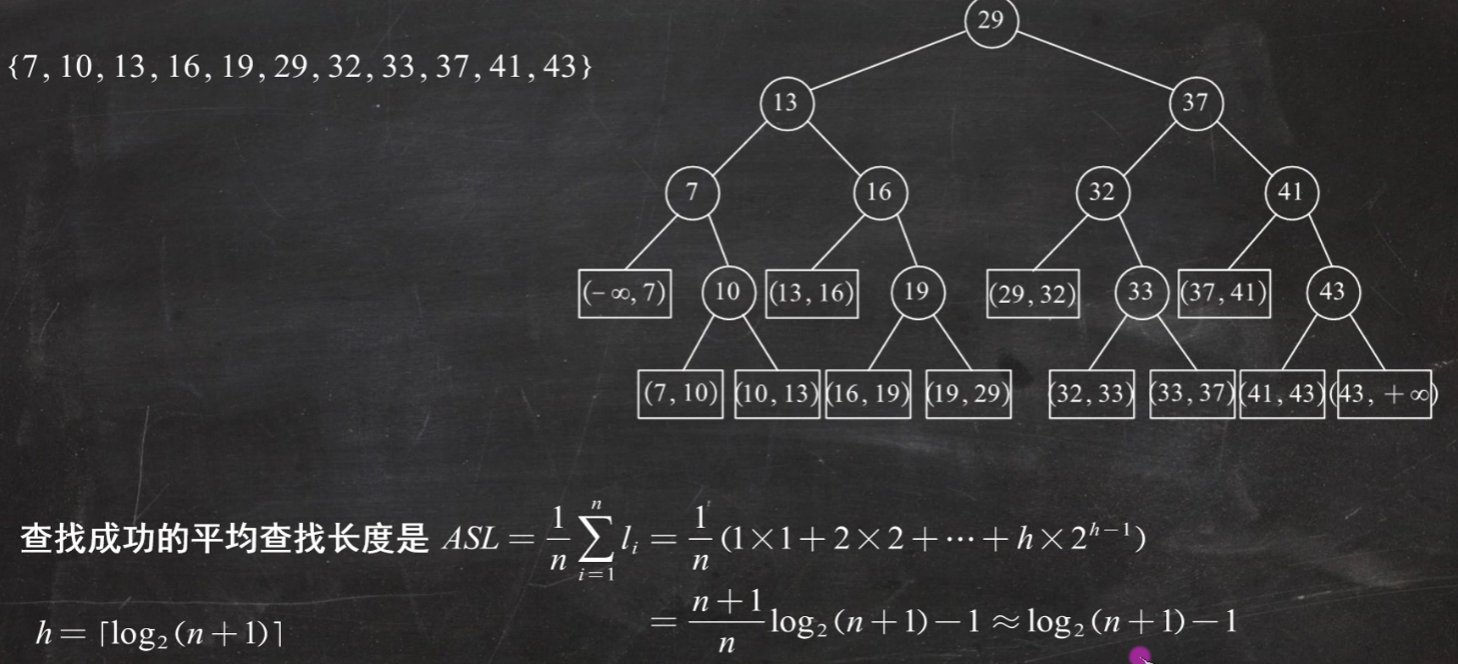
题1.二分查找要求结点（）
A. 有序、顺序存储
B. 有序、链式存储
C. 无序、顺序存储
D. 无序、链式存储
答案：A
题2.采用对分查找序列数据(6,15,30,37,65,78,89,90,97),若查找元素89时比较次数为（）

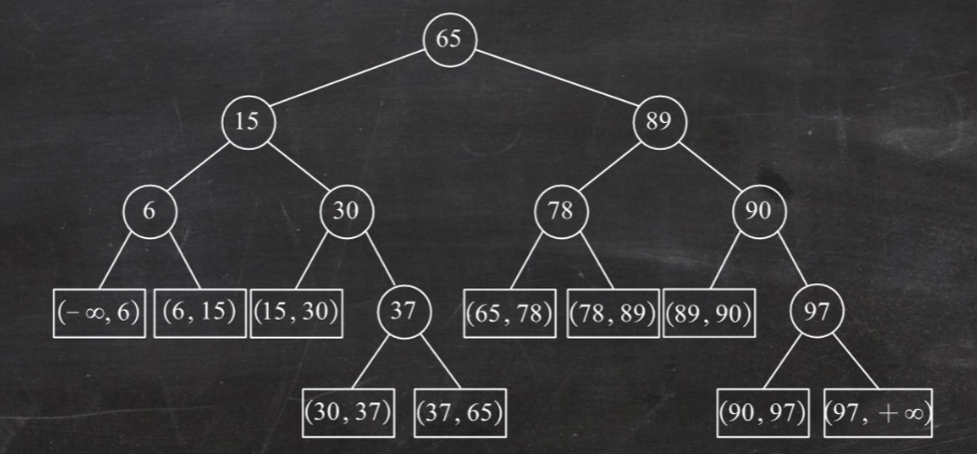
答案：2

实训

题目：

本关任务：编写程序，实现有序顺序表上的折半查找。
相关知识
实训中的类型定义及子函数的作用如下：
（1）定义顺序表中数据元素类型;
typedef int ElemType;
typedef int KeyType;
typedef struct
{ KeyType key;    //存放关键字
  ElemType data;    //其他数据
} SqType;
（2）子函数Create_SSTable(SqType R[]) ，实现查找表的创建，从键盘上依次输入有序的整型数据元素，创建查找表;
（3）子函数BinSearch(SqType R[],int n,KeyType k)，实现折半查找;
（4）子函数Show_End(int result,int testkey)，输出查找的结果；
（5）主函数，在主函数中调用上述子函数，输出相应的结果。

答案：

#include<iostream>
using namespace std;
#define MAXSIZE 8
#define OK 1;
typedef int ElemType;
typedef int KeyType;
typedef struct
{ KeyType key;  //存放关键字
    ElemType data;  //其他数据
} SqType;
  
int Create_SSTable(SqType R[])
{
    for(int i=0;i<MAXSIZE;i++)
    {cin>>R[i].key; }
    return 1;
}
  
int BinSearch(SqType R[],int n,KeyType k)
{ //请在这里补充代码，完成折半查找。
    int low=0,high=n-1,mid;
    while(low<=high)
    {
        mid=(low+high)/2;
        if(R[mid].key==k)return mid+1;
        else if(R[mid].key>k)high=mid-1;
        else low=mid+1;
    }
    return 0;
}
  
void Show_End(int result,int testkey)
{
    if(result==0)
        cout<<"未找到"<<testkey<<endl;
    else
        cout<<"找到"<<testkey<<"位置为"<<result<<endl;
}
int main()
{
    SqType R[MAXSIZE];
    Create_SSTable(R);
    int n=sizeof(R)/sizeof(R[0]);
    int testkey1,testkey2,result;
    cin>>testkey1;
    result=BinSearch(R,n,testkey1);
    Show_End(result,testkey1);
    cin>>testkey2;
    result=BinSearch(R,n,testkey2);
    Show_End(result,testkey2);
    return 0;
}

散列表

散列函数： $Hash(key) = Addr$
同义词： 散列函数可能会把两个或两个以上的不同关键字映射到同一地址
（1）直接定址法： $H(key) = key$ $H(key) = a \times key + b$
（2）除留余数法： 取一个不大于但最接近或等于 $m$ 的质数 $p$ 公式：$H(key) = key % p$
（3）数字分析法
（4）平方取中法

例题：

线性探测就是往后一个一个挪

注意不成功：地址个数就是取模的后面那个数，前面的是对应空的比较次数（0就是1次，1相距最近的空位置距离为13，2为12，依次类推）
存放方式：拉链法，用线性链表存储

二次探测法：

by 梁家诺