svm(support vector machine)之svr(support vector regression)学习笔记(?)

1.SVR和SVC的区分：
　　SVR：构建函数拟合数据；SVC：二向数据点的划分(分类)
　　注：SVR的是输入时给出的实际值 $y_{i}$，SVC的 $y_{i}$是输入时给出的类别，即+1，-1。
2.SVR的目的：
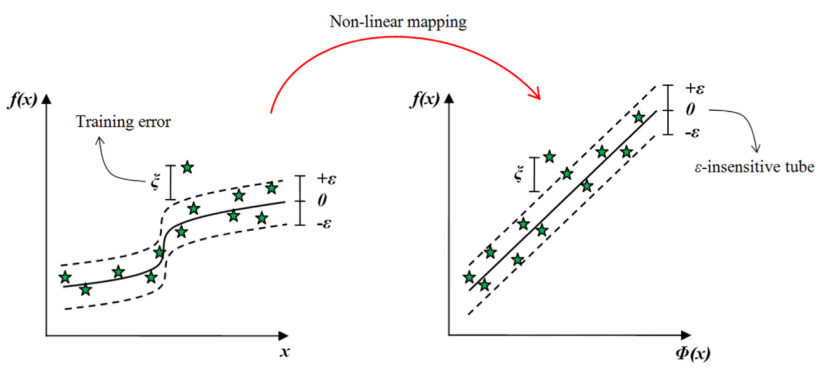
　　找到一个函数$f(x)$，使之与训练数据给出的实际目标$y_{i}$ 的偏差几乎不超过$ε$，同时尽可能平坦。

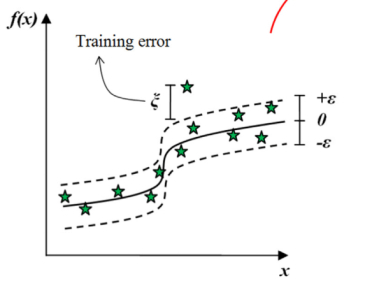
　　如图，形成了$ε－$不敏感区间。
3.间隔：
　　分为软间隔和硬间隔。
　　对于SVR来说，硬间隔是点全部落在$ε－$不敏感区间；软间隔是允许少量点落在区间外，编号为$i$的点的误差$\xi _{i}$ 定义式为：
　　$\xi _{i}＝ \left\{ \begin{aligned} %\nonumber &0&&y_{i} \in[f(x_{i})-\varepsilon ,f(x_{i})+\varepsilon],&\\ &f(x_{i})-\varepsilon-y_{i}&&y_{i} \in(-\infty ,f(x_{i})-\varepsilon),&\\ &y_{i}-f(x_{i})-\varepsilon&&y_{i} \in(f(x_{i})+\varepsilon ,+\infty).&\\ \end{aligned} \right.$
　　即点落在区间外面误差才有值。
　　为了统一定义，咱们设两个误差变量$\xi _{i}^{+}$ 和 $\xi _{i}^{-}$ ,
　　将定义改为：
$\xi _{i}^{+}＝\left\{ \begin{aligned} &0&&y_{i} \in(-\infty ,f(x_{i})+\varepsilon],&\\ &y_{i}-f(x_{i})-\varepsilon&&y_{i} \in(f(x_{i})+\varepsilon ,+\infty).&\\ \end{aligned} \right.\\$

$\xi _{i}^{-}＝ \left\{ \begin{aligned} &f(x_{i})-\varepsilon-y_{i}&&y_{i} \in(-\infty ,f(x_{i})-\varepsilon),&\\ &0&&y_{i} \in[f(x_{i})-\varepsilon ,+\infty).&\\ \end{aligned} \right.$

4.逼近函数的表示方法：
　　高维：
　　

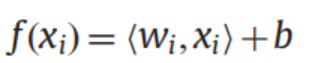
　　用核函数在低维空间表示内积：
　　

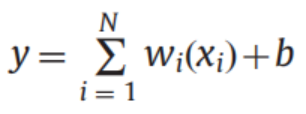
　　注：<,>是求内积的符号；超平面的一般方程为：$\overrightarrow{w^{T}} \overrightarrow{x_{i}} +b=0$,其中$\overrightarrow{w^{T}}$和$\overrightarrow{x_{i}}$都为向量，$\overrightarrow{x_{i}}$为输入的一个数据$i$的ｎ个特征汇总成的ｎ维特征向量。(后面的向量符号可能省略，但还是指同样的东西)
５.损失函数：$ε－$不敏感损失函数
　　
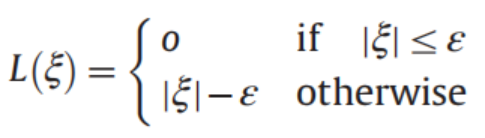
　　将我们定义的$\xi _{i}^{+}$ 和 $\xi _{i}^{-}$代入，发现：
　　$L(y _{i})=\xi_{i}^{+} /\xi_{i}^{-}$
　　将其引申，我们可以得出正则化风险的式子：
６.正则化风险最小化公式：
　　
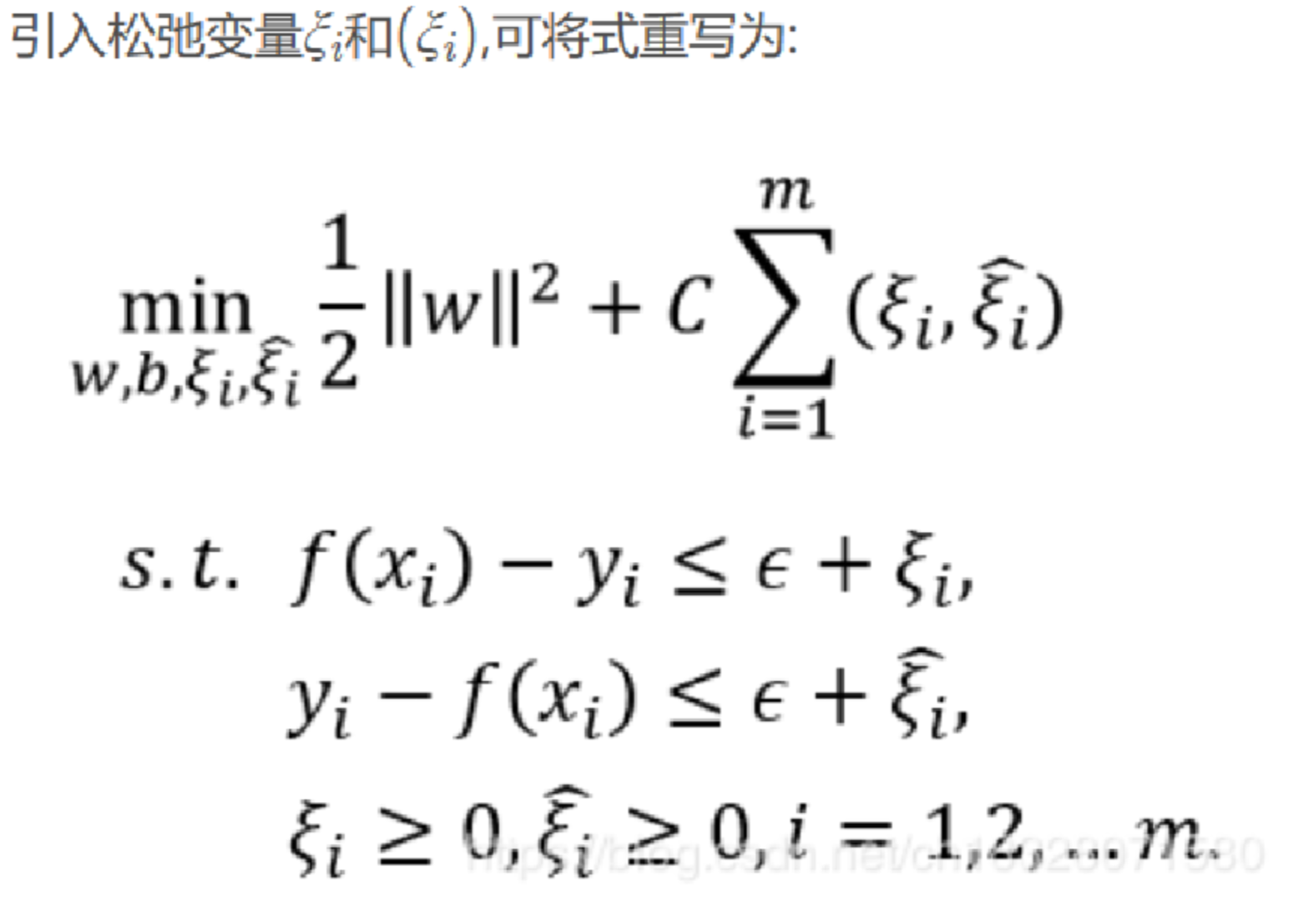
　　注：这里的$\xi_{i}$和$\widehat{\xi_{i}}$对应的是$\xi _{i}^{-}$ 和 $\xi _{i}^{+}$。
　　第一项为结构风险(正则化风险)，第二项为经验风险。
　　数据点满足“落在包含误差的区间”。
　　注：“|| ||”为向量的模
　　理解：$ε$是纵坐标的宽度，即超平面上方$ε$的点到同一横坐标的点的距离，
　　实际的垂直宽度$d=\frac{|\overrightarrow{w^{T}} \overrightarrow{x} +b|}{\left \|\overrightarrow{w} \right \|}=\frac{\varepsilon }{\left \|\overrightarrow{w} \right \|}$;
　　SVR要在最大化宽度的同时最小化风险，故要最小化$\left |\overrightarrow{w} \right |^{2}$。
　　 $\xi _{i}^{+}$ 和 $\xi _{i}^{-}$是超出不敏感区域的大小，惩罚系数为C
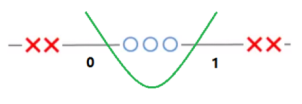
7.核技巧：通过将低维线性不可分数据转换到高维空间，使之线性可分。
　　
　　
　　
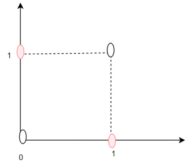
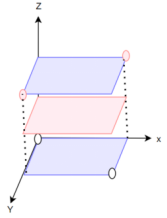
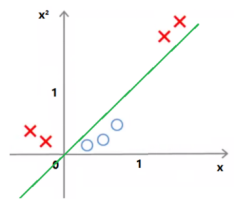
8.核函数的作用：
　　在希尔伯特空间中，核表示类似于内积，因此可以用低维的核函数表示高维空间的内积，
　　即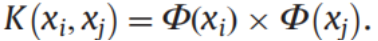
9.RBF/径向基函数/高斯核函数：
　　
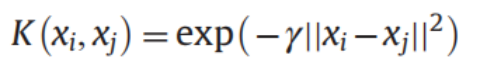
　　需要注意的是：按我的理解，对于每个$x_{i}$都会与其他所有的$x$进行核函数的内积操作，使得第ｉ个数据从　ｎ个ｍ维向量　变为　$n\times n$个值
10.KKT/拉格朗日函数的构建：
　　具体的条件和证明就不复述，之前写过KKT的学习笔记。
　　引入拉格朗日乘子：$\mu _{i}$和$\alpha _{i}$，将不等式约束条件转化相加，得到：
　　
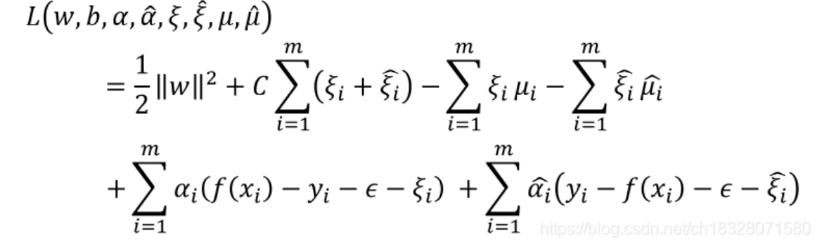
　　注：这里的$\xi_{i}$和$\widehat{\xi_{i}}$对应的是$\xi _{i}^{-}$ 和 $\xi _{i}^{+}$。
　　于是任务就变为：寻找合适的$\overrightarrow{w}$和$b$，使得式子的值最小。
　　
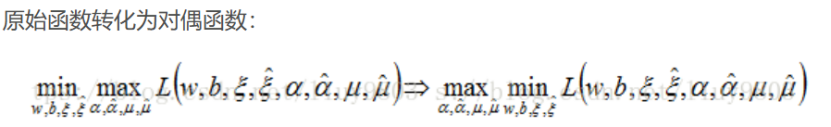
　　P.　max怎么插入的？：
　　Q.　$+\mu _{i}g(x)$中$\mu _{i}\ge 0,g(x)\le 0$,故　原式=max ［原式$+\mu _{i}g(x)$］。
　　注：$g(x)$指不等式约束条件。
　　然后，这里引入对偶的概念：
　　对偶分为强对偶性和弱对偶性。
　　弱对偶性是指：所有这样的式子都有的，对所有这样的式子的生效的，凤尾恒大于鸡头的性质。
　　即：$min max \ge max min$
　　而强对偶性是指：部分式子拥有的性质，即两边取等于号，可互相转换。
　　此处式子有强对偶性。（具体为什么有去看别人的证明吧……）
　　
　　$\sum_{i=1}^{n} \alpha _{i}=\sum_{i=1}^{n} \widehat{\alpha _{i}}$
　　$C=\mu _{i}+\alpha _{i}=\widehat{\mu _{i}} +\widehat{\alpha _{i}}$
　　

　　其中第一个，第二个，第四个都为互补松弛性条件。
　　第三个是分情况讨论得来的(后面有证)。
　　至于约束条件就是约束的不等式，站点条件就是求偏导等于０，
　　还需要满足对偶可行性条件：
　　即：$\widehat{\alpha _{i}} \ge 0,\alpha _{i} \ge 0,\widehat{\mu _{i}} \ge 0,\mu _{i}\ge 0$
　　
　　
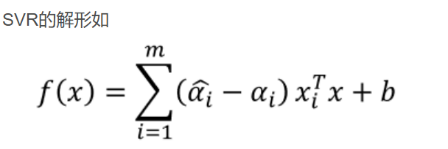
　　最后将求得的等式反代回去：
　　
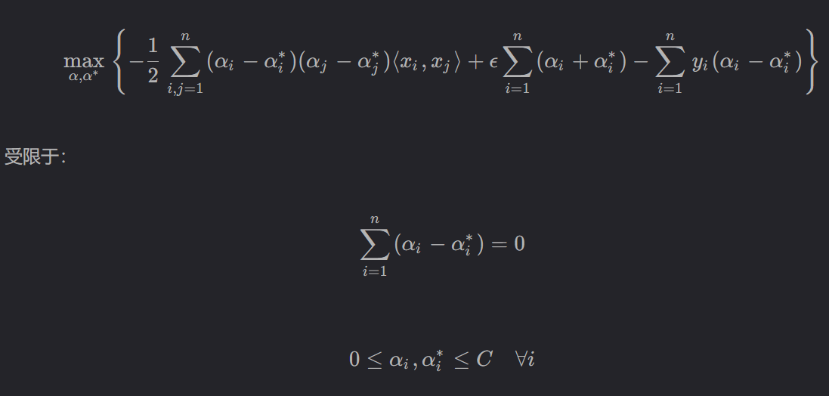
　　这个问题需要SMO来解，可能会在SMO的学习笔记再写。
11.关于支持向量的判别：
　　由于：
　　
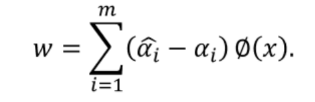
　　故$\widehat{\alpha _{i}} －\alpha _{i}\ne ０$的对$w$有贡献，为支持向量。
　　分类讨论：(不妨假设点一直在偏下方)
　　(1)点在不敏感区域内：
　　　此时$\xi_{i}=0,f(x)-y_{i}-\varepsilon -\xi_{i}=0$,
　　　故$\alpha _{i}=0$。
　　　同理：$\widehat{\alpha _{i}}=0$。
　　　$\widehat{\alpha _{i}} －\alpha _{i}=0$。
(2)点在不敏感区域边界上：
　　　此时$\xi_{i}=0,f(x)-y_{i}-\varepsilon -\xi_{i}=0,\alpha _{i}\ne0$。
　　　$\widehat{\xi_{i}}=0,y_{i}-f(x)-\varepsilon -\widehat{\xi_{i}}<0,\widehat{\alpha _{i}}=0$。
　　　$\widehat{\alpha _{i}} －\alpha _{i}\ne 0$。
　　　同时：$\xi_{i}=0,\mu_{i}>0,0<\alpha_{i}=C-\mu_{i}<C$。
(3)点在不敏感区域外：
　　　此时$\xi_{i}\ne0,f(x)-y_{i}-\varepsilon -\xi_{i}=0,\alpha _{i}\ne0$。
　　　$\widehat{\xi_{i}}=0,y_{i}-f(x)-\varepsilon -\widehat{\xi_{i}}<0,\widehat{\alpha _{i}}=0$。
　　　$\widehat{\alpha _{i}} －\alpha _{i}\ne 0$。
　　　同时：$\xi_{i}\ne0,\mu_{i}=0,\alpha_{i}=C-\mu_{i}=C$。
　　注：可以看出$\alpha _{i}\widehat{\alpha _{i}}=0,\xi _{i}\widehat{\xi _{i}}=0$。
　　这体现了：问题的复杂性独立于输入空间的维度，而仅取决于支持向量的数量。
12.$\alpha _{i}$的取值：
　　一般用SMO算法确定(SMO中说)。
13.$b$的取值：
　　可以用：

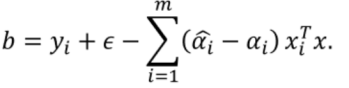
　　也可以：

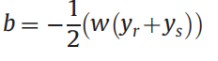
　　其中$y_{r}$和$y_{s}$是支持向量$x$，选择求取平均值。
　　后者更具鲁棒性。
14.训练SVR模型时需要的三个参数：
　　损失函数参数ε、惩罚项C和高斯核参数γ。
　　C被称为正则化常数，它决定了经验风险和正则化项之间的权衡，增加C的值将导致经验风险的相对重要性增加。
　　参数γ表示高斯核的方差，控制核函数的敏感性。可以理解为：γ越大，核函数值就越分立，差距越大，就会越倾向于凹凸不平，弯弯曲曲的分界线，对错误的容忍度更低；γ越小，核函数值就越接近，差距越小，就会越倾向于平坦，笔直的分界线，对错误的容忍度更高，甚至会出现分类错误的情况。
　　只要误差小于损失函数参数ε，就不关心误差，但任何大于此的偏差都不会被接受。