实验4
任务一:在任务一的程序中,一元二次方程的根无法设计成以函数数返回值的方式返回给主调函数。首先,教科书中提到“函数中允许有多个return语句,但每次只能有一个return语句被执行,即只能返回一个函数值”,这段话的意思就是我们可以通过条件语句出现多个return,但是函数的返回值只有一个,所有的return只有一个被执行。而一元二次方程的根有两个,与这条规则相违背。所以仅通过一个函数调用是无法实现的。但与此同时,我认为,对于这种需要输出多个结果,同时不同输出数据又与输入数据存在关联,可以设置两个函数调用,例如:此题可以用一个函数返回大根,另一个函数返回小根。
任务二:
#include <stdio.h>
long long fac(int n); // 函数声明
int main() {
int i,n;
printf("Enter n: ");
scanf("%d", &n);
for(i=1; i<=n; ++i)
printf("%d! = %lld\n", i, fac(i));
return 0;
}
// 函数定义
long long fac(int n) {
static long long p = 1;
p = p*n;
return p;
}
#include<stdio.h>
int func(int, int);
int main() {
int k=4,m=1,p1,p2;
p1 = func(k,m) ;
p2 = func(k,m) ;
printf("%d,%d\n",p1,p2) ;
return 0;
}
int func(int a,int b) {
static int m=0,i=2;
i += m+1;
m = i+a+b;
return (m);
}
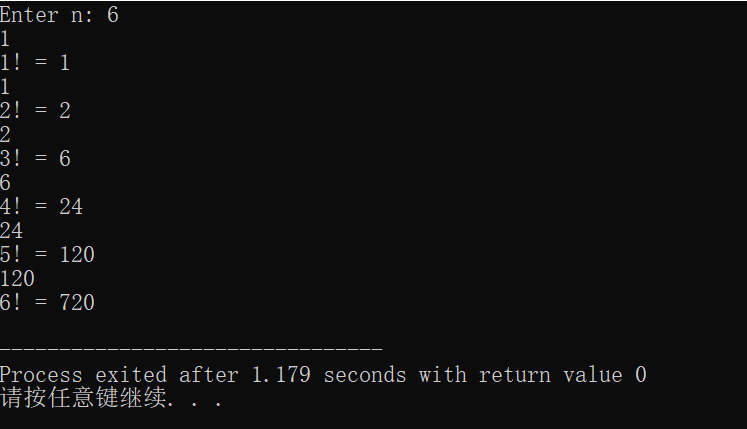
从理论分析,p1=(2+0+1)+4+1=8;p2=(3+8+1)+4+1=17。而运行结果也确实是8 17,与分析结果一致。关于局部static变量的特性:我认为相比于一般的局部变量,静态局部变量主要能在循环中或多次函数调用中保留每次变化后的值。另外一点,编译器会默认先对静态局部变量进行一次初始化,若在无赋值的情况下,所有静态局部变量初始化后的值为0。究其本质,一般的局部变量,往往在函数调用时可分配存储空间,而调用结束后即被释放,第二次再调用则要重新赋值。而局部static变量可被存储在静态存储区,从而保留上次的结果。
任务三:
#include <stdio.h>
#define N 1000
int fun(int n,int m,int bb[N]) {
int i,j,k=0,flag;
for(j=n;j<=m;j++) {
flag=1;
for(i=2;i<j;i++)
if(j%i==0) {
flag=0;
break;
}
if(flag!=0)
bb[k++]=j;
}
return k;
}
int main(){
int n=0,m=0,i,k,bb[N];
scanf("%d",&n);
scanf("%d",&m);
for(i=0;i<m-n;i++)
bb[i]=0;
k=fun(n,m,bb);
for(i=0;i<k;i++)
printf("%4d",bb[i]);
return 0;
}
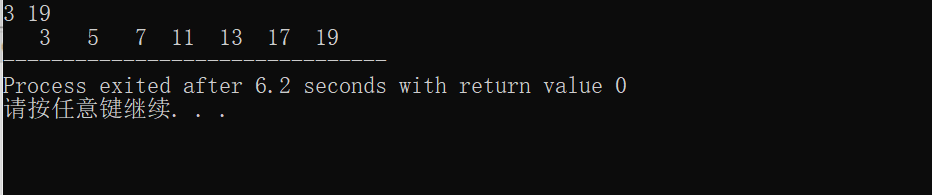
任务四:
#include <stdio.h>
long long fun(int n); // 函数声明
int main() {
int n;
long long f;
while(scanf("%d", &n) != EOF) {
f = fun(n); // 函数调用
printf("n = %d, f = %lld\n", n, f);
}
return 0;
}
// 函数定义
long long fun(int n)
{
long long f;
if(n==1)
{
f=1;
}
else
{
f=2*fun(n-1)+1;
}
return f ;
}
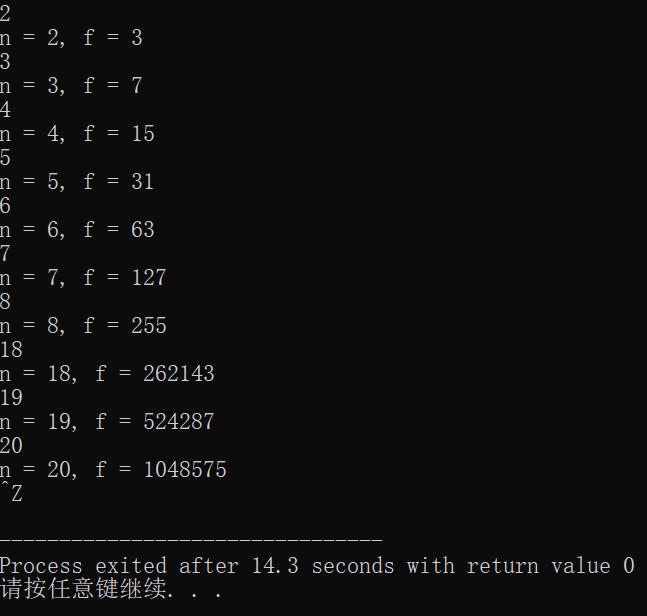
任务五:
#include <stdio.h>
void draw(int n, char symbol); // 函数声明
#include <stdio.h>
int main() {
int n, symbol;
while(scanf("%d %c", &n, &symbol) != EOF) {
draw(n, symbol); // 函数调用
printf("\n");
}
return 0;
}
// 函数定义
// 补足代码。。。
void draw (int n,char symbol)
{
int i,j;
for(i=1;i<=n;i++)
{
for(j=n-i;j>0;j--)
{
printf(" ");
}
for(j=1;j<=2*i-1;j++)
{
printf("%c",symbol);
}
printf("\n");
}
}
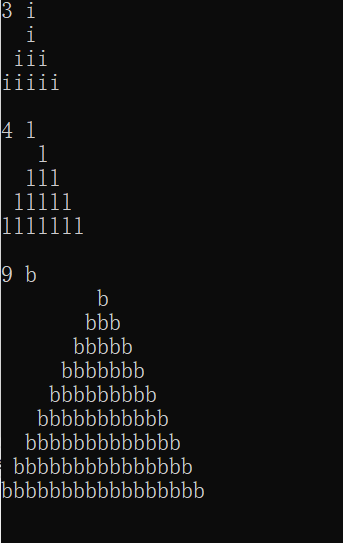
选做:
#include <stdio.h>
#define maxn 32
void jie (int n)
{
int i,k=0,j=0,WS=1;
int a[10000]={0};
a[0]=1;
for(i=0; i<n; i++)//进行n次与2乘法
{
int flag=0,count=0;
for(j=0;j<=WS;j++)//进行当前位数+1次乘法(如果有新进位便于进位)
{
a[j]=a[j]*2+flag;//该位数乘2,计算次数加一
flag=0;
if(a[j] >= 10)
{
flag=a[j]/10;
a[j]=a[j]%10;
}
if(a[WS]&&a[WS+1]==0) count=1;//当预留进位a[WS]发生进位并且前一位数是0时,进1位
else count =0;
}
WS+=count;
}
a[0]=a[0]-1;
for(i=WS-1; i>=0; i--)
{
printf("%d",a[i]);
}
printf("\n");
}
int main()
{
int n;
printf("enter a number:");
while(scanf("%d",&n)!=EOF)
{
jie(n);
printf("enter a number:");
}
return 0;
}
思路分析:(以上关于如何将超长数据赋给数组并进行各个位数的运算的代码来自网上的dl,我在此只进行思路的分析)
本算法的基本思路其实就是将一个很长的数据放在一个更长的数组当中,并通过循环嵌套实现各个位数的乘2运算以及相应的进位操作,当然里面还有许多小细节以确保循环的正常进行。
具体分析:首先设置一个很长的数组,例如:a[10000](注:此时数组的长度其实只要满足:10的长度次方比所求数据可能的最大值大即可)。关于位数的分配,本程序将个位分配给a[0],十位分配给a[1],依次类推。
然后是循环的嵌套:我们首先明确可能需要的循环:1,进行N次乘以2的运算 2,现有的所有位数乘以二的运算 3,按照顺序输出最后的数组结果
实际编译过程中,我们将 1循环(乘以二的运算)作为外圈的大循环,将 2循环嵌套在1循环中 。同时设置变量 ws 和 j 在数值增大的过程中实现位数的增加。变量flag用于存放进位的量,在次循环中普遍存放1(个位数乘以二的运算中结果不可能超过20)。
其中语句a[j]=a[j]*2+flag置于2循环的起首位置,实际上是应对现有最高位出现进位的情况,若无进位情况,默认也只是在更高位进行一次:0=0*2+0的运算而已。(实际循环中,这步的位置很关键,一般我们容易将进位的相关带入后续运算而导致错误),而flag=0的作用则是清除进位所存放的量。
另外if(a[j] >= 10) {flag=a[j]/10;a[j]=a[j]%10;}进行现有位数乘以二后的进位判断,即:判断是
否有哪个位数的值超过了9。
至于代码if(a[WS]&&a[WS+1]==0) count=1;else count =0;则用于进行现有最高位的判断,此时涉及到
位数的变换。当预留进位a[WS]发生进位并且前一位数是0时,进1位。、
最后配合循环1与循环2之间的累加语句,实现了每一次乘法运算中位数的变化。
而循环三独立于循环1和2,只是以逆序的方式输出数组,并以数组的形式表示数。
实验总结:
本次实验让我学会了用函数的形式完成前三章的许多代码,同时也理解了许多关于变量的新知识,
明确函数的使用,尤其是递归使用可以在一定程度上简化代码,甚至解决一些原先无法解决的问题
尤其是选做题目中,关于数组的应用,让我记忆尤深,网上的编程员运用了一些细节化的技巧就实
现了阻碍我许久的问题,让人惊叹!
踩的坑:并非所有问题都要巧用函数,也并非所有函数要使用递归。在有些题目中,刻意地使用
递归函数,却让我忽视了基本的循环语句的解决方法,在我看来,这是得不偿失的。
小问题:关于数组与函数的结合,在选做的题目中,如果要求循环输入数据,同时我将数组出现在主函数中
并以实参的形式赋值给另外的函数,在个别循环后,似乎数组的值被保存,导致输出结果的错误。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号