SSM

状态空间模型 (SSM)

状态空间模型（SSM），与Transformer和RNN一样，用于处理信息序列，例如文本和信号。

SSM 是用于描述这些状态表示并根据某些输入预测其下一个状态可能是什么的模型,然而，它不使用离散序列，而是将连续序列作为输入并预测输出序列

 

 

1.什么是状态空间？

状态空间是一组能够完整捕捉系统行为的最少变量集合。它是一种数学建模方法，通过定义系统的所有可能状态来表述问题。

 在语言模型中，我们经常使用嵌入或向量来描述输入序列的“状态”。

 在神经网络的语境中，“状态”通常指的是网络的隐藏状态。在大型语言模型的背景下，隐藏状态是生成新tokens的一个关键要素。

2.SSM公式来源

参考：https://www.bilibili.com/video/BV1n7421d7xG/?spm_id_from=333.337.search-card.all.click&vd_source=8e62d7fcd6fc4f51e61f64cd117a89c2

3.离散SSM和连续SSM对比

 4.离散化

 零阶保持技术：

 推导过程：

5.什么是状态空间模型？

状态空间模型（SSM）是用来描述这些状态表示，并根据给定的输入预测下一个可能状态的模型。

SSM是控制理论中常用的模型，在卡尔曼滤波、隐马尔可夫模型都有应用。它是利用了一个中间的状态变量，使得其他变量都与状态变量和输入线性相关，极大的简化问题。

状态空间模型（SSM）假定动态系统（比如在三维空间中移动的物体）的状态可以通过两个数学方程来预测，这两个方程描述了系统在时间t时的状态如何随时间演变。

 这两个方程构成了状态空间模型的核心。

A是存储着之前所有历史信息的浓缩精华(可以通过一系列系数组成的矩阵表示之)，以基于A更新下一个时刻的空间状态hidden state

注：“这里就是导数，是SSM 一阶微分方程 中的导数，这里还是连续型，不是离散型，毕竟只有在离散系统中才是t和t-1” 

总之，通过求解这些方程，可以根据观察到的数据：输入序列和先前状态，去预测系统的未来状态

SSM的关键是找到：状态表示(state representation)—— ，;以便结合「其与输入序列」预测输出序列；而这两个方程也是状态空间模型的核心( 一方面 ， A、B、C、D这4个矩阵是参数，是可以学习到的，二方面，学习好之后，在SSM中，矩阵A、B、C、D便固定不变了——即便是在不同的输入之下，但到了后续的改进版本mamba中则这4个矩阵可以随着输入不同而可变)

第一个方程：状态方程，

连续时间：用微分方程描述，对时间的导数。

离散时间：用差分方程描述，h(t-1)表示上一时刻状态。

状态方程展示了输入如何通过矩阵B影响状态，以及状态如何通过矩阵A随时间变化。

 h(t)指的是任何给定时间t的潜在状态表示，而x(t)指的是某个输入。

第二个方程：输出方程，描述了状态如何转换为输出(通过矩阵 )，

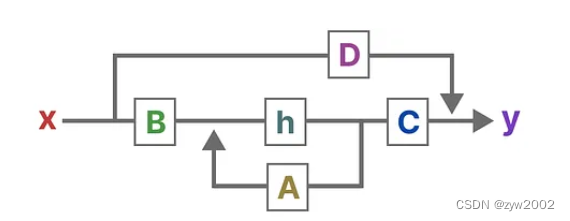
设想我们有一个输入信号x(t)，这个信号首先与矩阵B相乘，而矩阵B刻画了输入对系统的影响程度。更新后的状态（类似于神经网络的隐藏状态）是一个潜在空间，它包含了环境的核心“知识”。我们将这个状态与矩阵A相乘，矩阵A揭示了所有内部状态是如何相互连接的，因为它们代表了系统的基本动态。矩阵A在创建状态表示之前被应用，并在状态表示更新之后进行更新。利用矩阵C来定义状态如何转换为输出。</p><p>我们可以利用矩阵 D提供从输入到输出的直接信号。这通常也称为跳跃连接。

由于矩阵 D类似于跳跃连接，因此在没有跳跃连接的情况下，SSM 通常被视为如下,SSM通常被认为是不包含跳跃连接的部分。

 

简化视角

6.举例-离散SSM

7.时不变特性

之所以叫时不变（与时间无关），就是 ABCD参数是固定的，这当然是一种假设，而且是个强假设。D在许多实际系统中，它可以是零。很多人学 SSM渐渐就忘了这个强假设。Transformer本身是没有这样的假设的，也就是说可以用于时变系统和非线性系统。

牺牲通用性，换来特定场景下的更高性能，这就是所有SSM模型的最底层逻辑。

离散化：离散化主要是为了方便计算机处理。

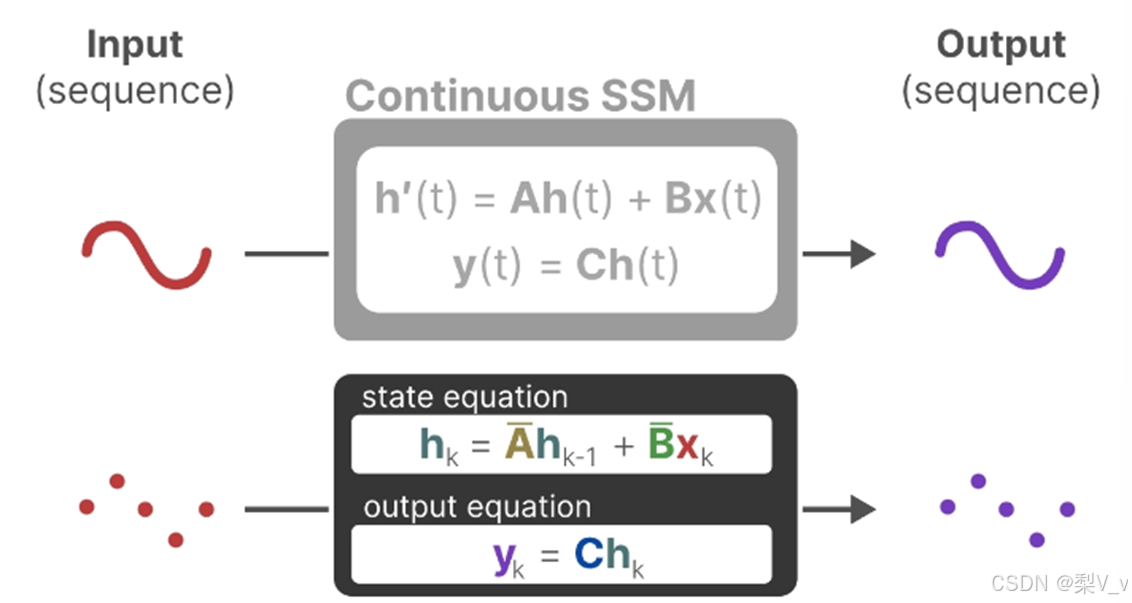
在实际应用SSM时，离散化是其核心思想。该架构的所有便利性都在于这一步，因为它使我们能够从SSM的连续视角传递到另外两个：递归视角以及卷积视角

 

 

 

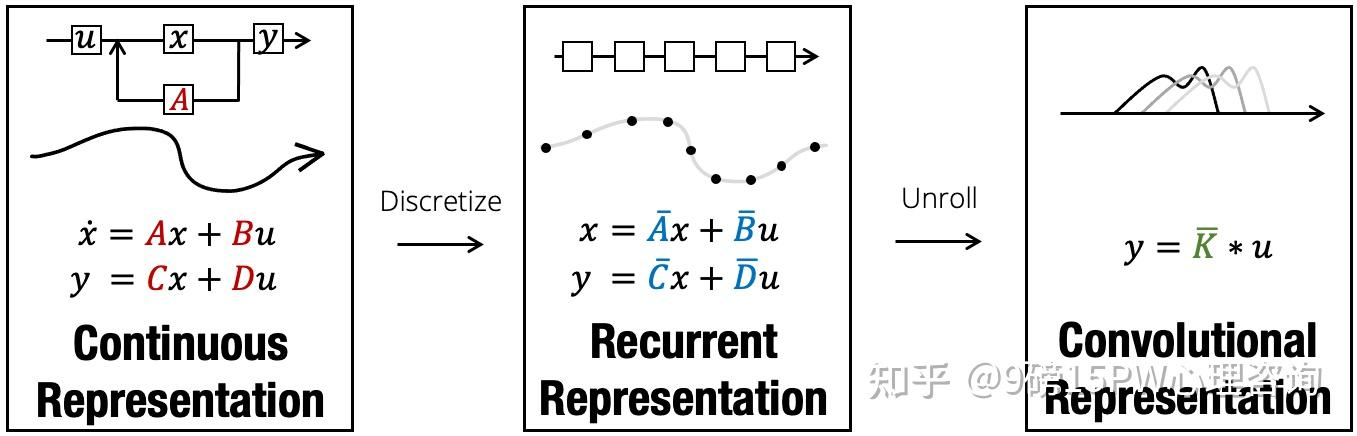
s4模型-structured state spaces for sequences

1.从SSM中获得启发，提出S4模型，将SSM引入深度学习领域

 

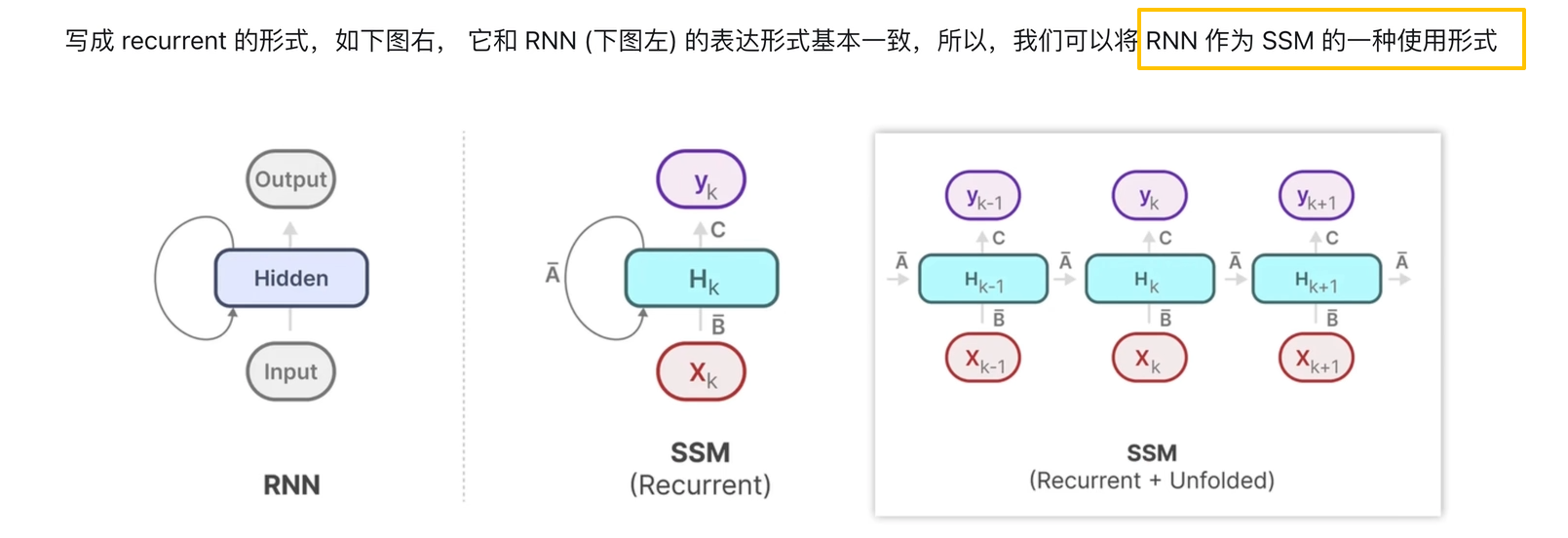
2.训练阶段使用SSM的卷积表示，推理阶段使用RNN的表示

 SSM的卷积表示

卷积知识：

 

 

 把SSM公式用卷积形式表示

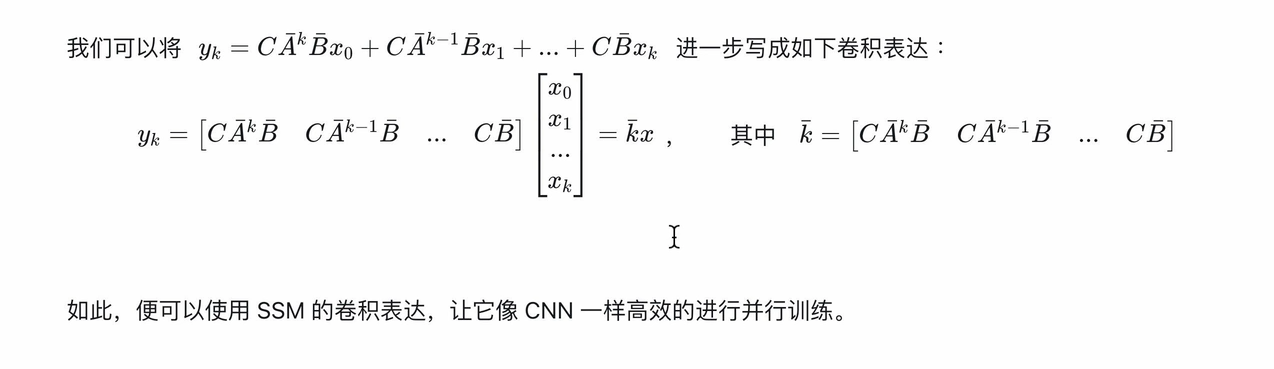
3.使用Hippo矩阵减小计算复杂度（即S4参数化），解决长距离依赖问题

A：

 

 

 

 

 

 LTI局限性

从循环的角度来看，它们的恒定动态，无法让它们从上下文中选择正确的信息，也无法以依赖于输入的方式影响沿序列传递的隐藏状态。

从卷积的角度来看，众所周知，全局卷积可以解决普通的复制任务 ，因为它只需要时间感知，但由于缺乏内容感知，它们难以完成选择性复制任务。更具体地说，输入到输出之间的间隔是变化的，无法用静态卷积核建模。

总而言之，序列模型的效率与有效性权衡取决于它们压缩状态的能力：高效的模型必须具有较小的状态，而有效的模型必须具有包含来自上下文的所有必要信息的状态。反过来，我们提出构建序列模型的一个基本原则是选择性：或者说，一种感知上下文的能力，能够聚焦或过滤掉序列状态中的输入。具体来说，选择机制控制着信息如何在序列维度上传播或交互

选择性SSM

 图的解释

把 5 个输入通道分别送进 5 个独立的 SSM，每个 SSM 内部只把「当前真正需要」的 4 维潜在状态 h 临时拉到 GPU 高速缓存（SRAM）里算一圈，算完就扔，绝不占主存（HBM），靠「选择机制」决定哪一段 h 才值得被实例化

 

通过“参数化SSM的输入”，让模型对信息有选择性处理，以便关注或忽略特定的输入。这样一来，模型能够过滤掉与问题无关的信息，并且可以长期记住与问题相关的信息

好比，Mamba每次参考前面所有内容的一个概括，越往后写对前面内容概括得越狠，丢掉细节、保留大意

SSM的循环表示创建了一个非常高效的小状态，因为它压缩了整个历史记录。然而，与不压缩历史记录（通过注意力矩阵）的Transformer模型相比，它的功能要弱得多。

Mamba的目标是实现两全其美：创建一个像Transformer一样强大的小状态。Mamba通过有选择地将数据压缩到状态中来实现这一目标。当输入一个句子时，通常会包含一些没有多大意义的信息，例如停用词。为了有选择地压缩信息，我们需要参数依赖于输入。为此，我们首先探讨训练期间SSM中输入和输出的维度。

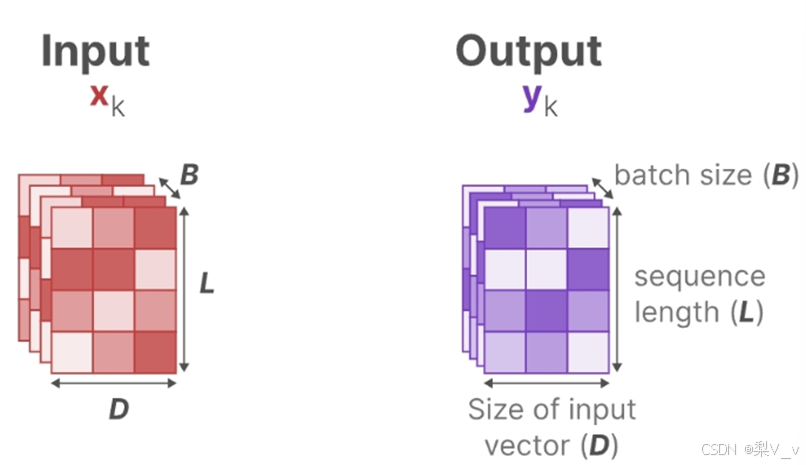
为了对批量大小为B，长度为L，具有D个通道的输入序列𝑥进行操作。总之，类似总计有B个序列，每个序列的长度为L，且每个序列中每个token的维度为D。

在结构化状态空间模型 (S4) 中，矩阵A、B和C独立于输入，因为它们的维度N和D是静态的并且不会改变。  A∈R^N×N,B∈R^N×1,C∈R^1×N矩阵都可以由𝑁个数字表示。

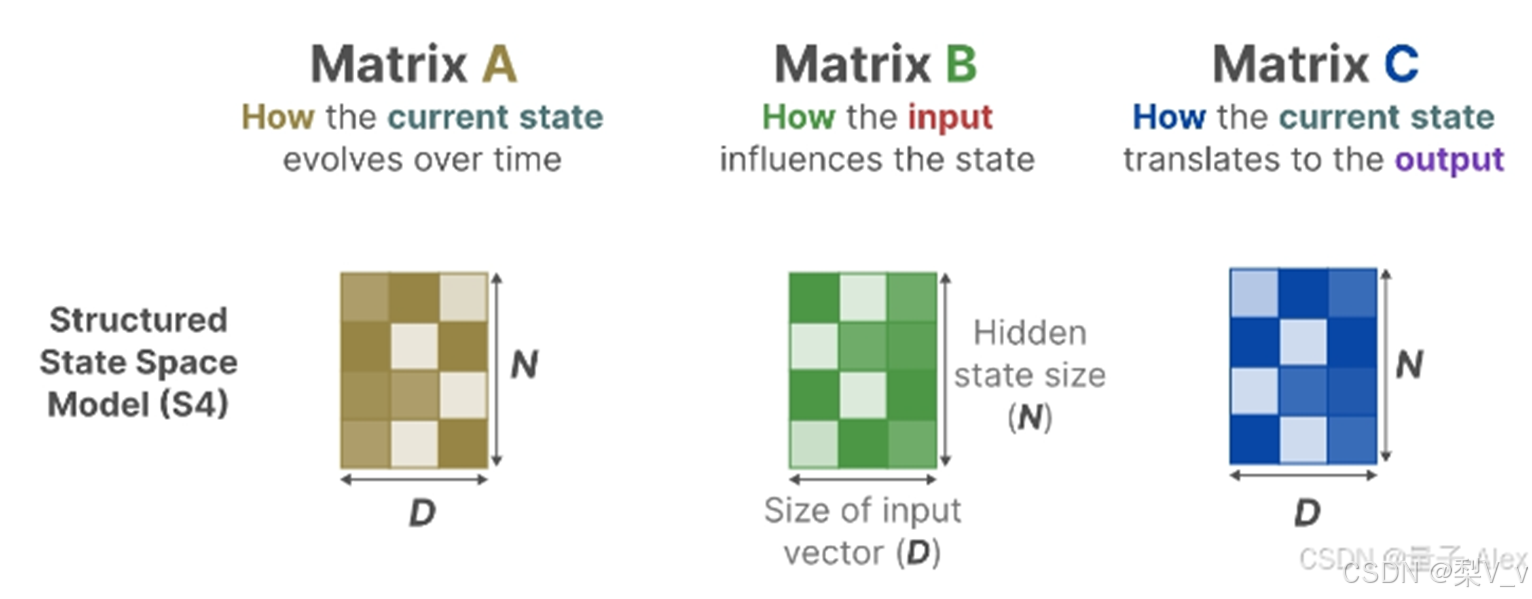
 从S4到S6的过程中 影响输入的𝐵矩阵、影响状态的𝐶矩阵的大小从原来的(D,N)变成了(B,L,N) batch size、sequence length、hidden state size

且Δ的大小由原来的D变成了(B,L,D)，意味着对于一个 batch 里的每个 token (总共有 BxL 个)都有一个独特的Δ

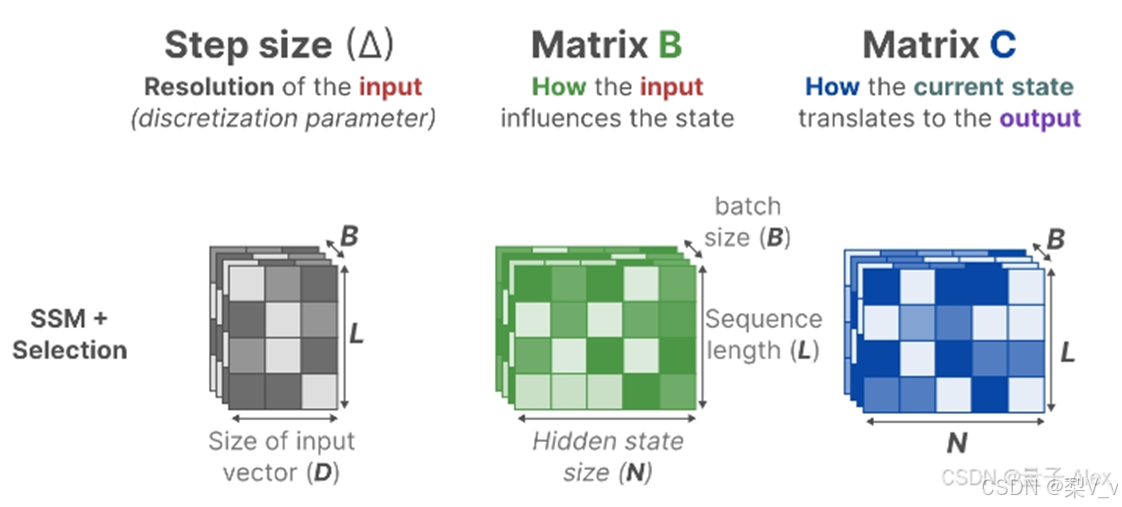
 Mamba通过合并输入的序列长度和批量大小，使得矩阵B和C以及步长Δ都取决于输入。这意味着对于每个输入标记，我们现在有不同的B和C矩阵，可以解决内容感知问题！

A没有变成依赖于输入，但是离散化之后也是可变的，因为diate可变