DP优化

优化DP笔记

P6040 「ACOI2020」课后期末考试滑溜滑溜补习班

设 \(f_i\) 表示老师解决到第 \(i\) 个学生需要最少的精力，答案显然是 \(f_n\)

边界 : 对于 \(i=1\) , \(f_1=a_1\)

对于其他的 \(i\) 号学生，我们假设老师是从第 \(j\) 位学生过来的，所以状态转移方程分为三项

1. \(f_j\) 表示之前的值
2. \((i-j-1)\times d+k\) 表示应对调侃和移动花费的精力
3. \(a_i\) 是解决当前学生问题花费的精力

整合起来方程就为

\[f_i=\min \{f_j+(i-j-1)\times d+k+a_i\} \]

当然 \(j\) 是有范围的 \(i-x≤j<i\) 当 \(j=i-1\) 时，实际上就是没有跳过

对于每个\(f_i\) ,只需要寻找最小的 \(f_j\) 转移过来就可以了，但这样要循环 \(i\) 和 \(j\) ，时间复杂度为 \(O(n^2)\)

然后对于 \([i-x,i-1]\) 的区间内寻找最小值，我们可以用单调队列可以维护求出来

把 \(f_j\) 提出来即可

\[f_i=a_i+k+(i-1)\times d+\min\{dp_j-j\times d\} \]

接下来我们维护 \(f_j-j \times d\)

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e7 + 10;
inline int read()
{
    int x = 0, f = 1;
    char s = getchar();
    while (s < '0' || s > '9')
    {
        if (s == '-')
            f = -f;
        s = getchar();
    }
    while (s >= '0' && s <= '9')
    {
        x = (x << 3) + (x << 1) + (s ^ 48);
        s = getchar();
    }
    return x * f;
}

LL n, k, d, x, tp, seed;
LL a[N], q[N], f[N];
inline LL rnd()
{
    static const int MOD = 1e9;
    return seed = (1LL) * (seed * 0x66CCFF % MOD + 20120712) % MOD;
}

int main()
{
    cin >> n >> k >> d >> x >> tp;
    if (tp)
    {
        seed = read();
        for (int i = 1; i <= n; i++)
            a[i] = rnd();
    }
    else
    {
        for (int i = 1; i <= n; i++)
            a[i] = read();
    }
    f[1] = a[1];
    int head = 1, tail = 1;
    q[1] = 1;
    for (int i = 2; i <= n; i++)
    {
        while (head <= tail && q[head] < i - x)
            head++;
        f[i] = f[q[head]] + a[i] + k + (i - q[head] - 1) * d;
        while (head <= tail && f[q[tail]] - q[tail] * d >= f[i] - i * d)
            tail--;
        q[++tail] = i;
    }
    cout << f[n] << endl;
    return 0;
}

P2168 [NOI2015] 荷马史诗

这道题的本体为哈夫曼数。

以二叉哈夫曼树为例，给 \(n\) 个点，构造一棵哈夫曼树，每次选剩下的两棵权值最小的树合并成一棵新树，新树的根权值等于前两棵合并的树的根权值和

例如下图

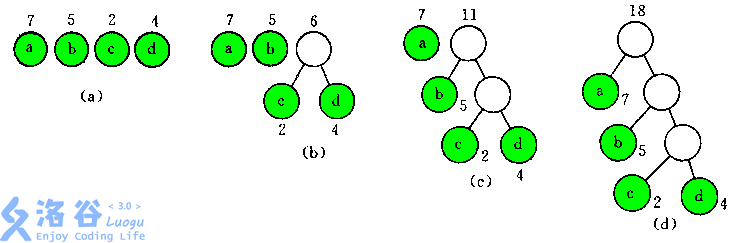
(a图):四个点 \(a,b,c,d\),权值分别为\(7,5,2,4\)

(b图):先把 \(2(c)\) 和 \(4(d)\) 合并，新的根节点值为 \(6\)

(c图):再把 \(5(b)\) 和 \(6(c+d)\) 合并，新的根节点为 \(11\)

(d图):最后把 \(7(a)\) 和 \(11(b+c+d)\) 合并，新的根节点为 \(18\)

那么这道题便是 \(k\) 叉哈夫曼树，但如果真正去写就会发现一种情况：

当最后一次合并之后，可能树上只剩下 \(m\) 个节点，且 \(1<m<k\) 无法再合并

所以我们可以用补点的方法这个方法：

首先，我们每次合并用掉 \(k\) 个值又合并出来一个值，那么按每次合并来算，我们每次用掉了 \(k-1\) 个值，然后，我们最终需要只剩 \(1\) 个值，也就是需要合并 \(n-1\) 个值，所以我们只要判断 这个东西\((n-1)\mod (k-1)=0\) 成立，我们还需要补 \((k-1)-((n-1)\mod (k-1)\) 个点

接下来我们看一个例子

原文为:\(AMCADEDDMCCAD\)

我们发现只有五个字母 \(E,M,C,A,D\) ,使用频率为 \(\{1,2,3,3,4\}\)

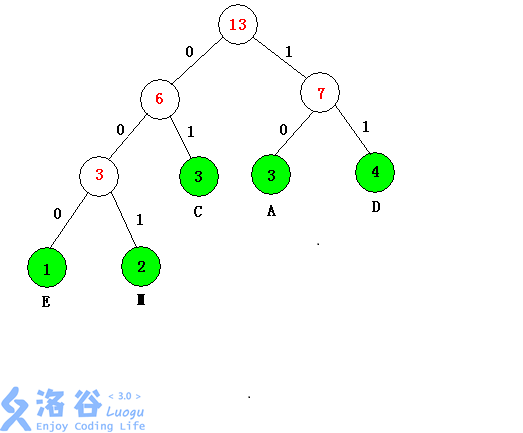
绿色为原来的点，白色为补点，\(0\)，\(1\) 表示左右儿子

哈夫曼编码为

\(E=000,I=001,C=01,A=10,D=11\)

答案为树的所有叶子节点的带权路径长度之和与树的最大深度

因为Huffman每次合并都要排序，所以使用堆（直接用priority_queue更方便）。

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

struct node
{
    LL w, h; //表示权值和高度
    bool operator<(const node &x) const
    {                 //重载运算符
        if (w != x.w) //优先考虑权值
            return w > x.w;
        return h > x.h;
    }
};
priority_queue<node> haff;

LL n, k, ans1, ans2, x; //单词数量、进制
//重新编码以后的最短长度、最长字符串s[i]的最短长度

int main()
{
    cin >> n >> k;
    for (int i = 1; i <= n; i++)
    {
        cin >> x;
        haff.push(node{x, 1}); //默认高度为1
    }
    if ((n - 1) % (k - 1)) //判断是否需要补点
    {
        x = k - 1 - (n - 1) % (k - 1); //要补的点数
        for (int i = 1; i <= x; i++)
            haff.push((node){0, 1}); //补点
    }
    LL sum, maxx;            //临时答案
    while (haff.size() != 1) //因为不可以是负数，所以大于1个点就跑
    {
        sum = 0, maxx = -2147483646;
        for (int i = 1; i <= k; i++) //每次选出k个数
        {
            sum += haff.top().w;            //加上队首
            maxx = max(haff.top().h, maxx); //找最小长度
            haff.pop();                     //队头出队
        }
        haff.push((node){sum, maxx + 1}); //加上合并的值
        ans1 += sum;
        ans2 = max(ans2, maxx);
    }
    cout << ans1 << endl << ans2;
    return 0;
}

「DPOI-1」道路规划

[USACO04DEC] Dividing the Path G