LCA 最近公共祖先

题目传送门

LCA和我们昨天讲的ST表一样采用了倍增思想，所以预处理时间复杂度为 \(O(n \log n)\) ,查询时间复杂度\(O(\log n)\) 。

1.预处理

首先我们得预处理出两个数组

1. \(fa\) 数组, \(fa_{i,k}\) 表示的是从 \(i\) 这个结点出发，向上走 \(2^k\) 步所能走到的节点。
2. \(depth\) 数组，\(depth_i\) 表示深度和层数。

来看一颗树

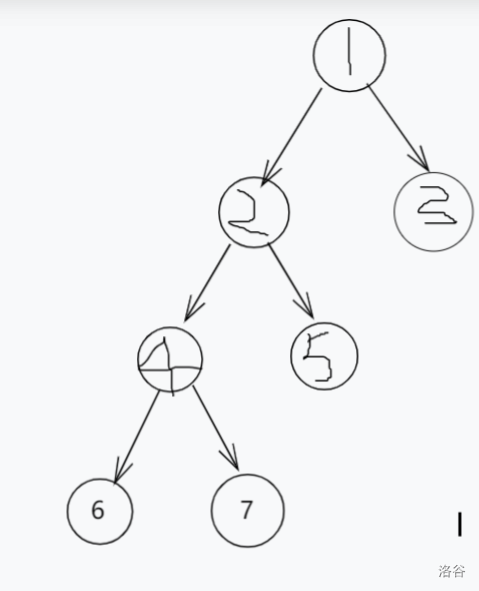
那对于叶子节点 \(6\), \(fa\) 数组为

\(fa_{6,0} = 4\)

\(fa_{6,1}=2\)

\(fa_{6,2}=NULL\)

我们如何初始化？很简单,我们分两种情况讨论

1. \(j=0\) 这时候 \(fa_{i,j}=\)i的父节点
2. 这时候我们先跳到上一次跳到的地方 \(fa_{i,j-1}\) ,再跳 \(j-1\) 步就到了，则 \(fa_{i,j}=fa_{fa_{i,j-1},j-1}\)

这是 \(fa\) 数组的初始化

再来看看 \(depth\) 的初始化，首先我们设置哨兵，然后层数就等于上一层加上一个 \(1\)

2.查询

为方便处理 当 \(a\) 在 \(b\)上面时 把 \(a,b\) 互换

步骤一，把深度更深的 \(a\) 跳到 \(b\) ,我们这里判断 \(depth_{fa_{a,k}}>depth_b\)的时候就继续跳

步骤二, \(a,b\) 两个一起跳，最后再跳一步，(越界怎么办？假如a,b都跳出根节点,\(fa_{a,k}==fa_{b,k}==0\) 不符合更新条件)

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 1e4 * 4 + 10, M = N * 2;
int n,m;
int h[N], e[M], ne[M], idx;
int depth[N];//深度
int fa[N][16];//表示从i开始,向上走2^j步所能走到的结点
int q[N];

void add(int a, int b)  // 添加一条边a->b
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void bfs(int root)//预处理
{
    memset(depth, 0x3f, sizeof depth);
    depth[0] = 0, depth[root] = 1;
    int hh = 0, tt = 0;
    q[0] = root;
    while(hh <= tt)
    {
        int t = q[hh ++ ];
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(depth[j] > depth[t] + 1)//没有搜索过
            {
                depth[j] = depth[t] + 1;
                q[ ++ tt] = j;
                fa[j][0] = t;
                for (int k = 1; k <= 15; k ++ )
                    fa[j][k] = fa[fa[j][k - 1]][k - 1];//fa[j][k - 1] 先跳到上一个跳的位置，但这只是一半，所以再条k-1
            }
        }
    }
}

int lca(int a, int b)
{
    if(depth[a] < depth[b]) swap(a, b);
    for (int k = 15; k >= 0; k -- )
    {
        if(depth[fa[a][k]] >= depth[b])
            a = fa[a][k];
    }
    if(a == b) return a;
    for(int k = 15; k >= 0; k --)
    {
        if(fa[a][k] != fa[b][k])
        {
            a = fa[a][k];
            b = fa[b][k];
        }
    }
    return fa[a][0];
}

int main()
{
    scanf("%d", &n);
    memset(h, -1, sizeof h);
    int root = 0;
    for (int i = 0; i < n; i ++ )
    {
        int a,b;
        cin >> a >> b;
        if(b == -1)
            root = a;
        else add(a, b), add(b, a);
    }
    bfs(root);
    scanf("%d", &m);
    while(m -- )
    {
        int a,b;
        scanf("%d%d", &a, &b);
        int p = lca(a, b);
        if(p == a) puts("1");
        else if(p == b) puts("2");
        else puts("0");
    }
    return 0;
}