ST 表学习笔记

ST 表，可以用来做区间最值问题， 我们这里用来做区间的最大值，时间复杂度可以达到\(O(n \log n)\)预处理，\(O(1)\)查询答案。

基本思路

我们首先会想到的是设

\(maxx_{i,j}\) 为左端点为 \(i\) ,右端点为 \(j\) 的区间内的最大值，状态转移方程为\(maxx_{i,j} = \max(maxx_{i,j-1},a_j)\)

然后我们可以使用 ST 表来解决

首先我们会发现一个规律:\(\max(x,y,z)=\max(\max(x,y),\max(y,z))\)

那我们就可以采用一个倍增的思想：设 \(f_{i,j}\) 为左端点为 \(i\) ,长度为 \(2^j\) 的区间最大值，我们可以根据刚才的结论将刚刚的区间进行二分操作，就可以得到状态转移方程

\[f_{i,j}=\max(f_{i,j-1},f_{i+2^{j-1},j-1}) \]

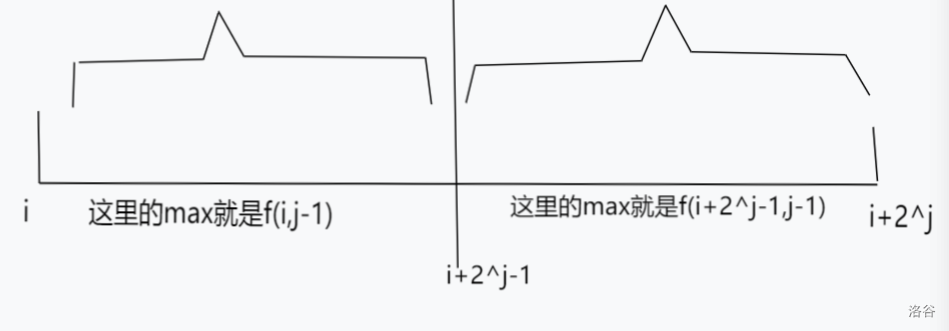
注意，右端点( \(i+2^j\) )不能越界,那这样的话以每一个起点开始就会拆分成 \(\log(n)\) 个区间,每个区间的话也能够用 \(O(1)\) 查询。

那么如何查询？

很简单，我们设做右端点为 \(l,r\) ,长度为 \(len\) ，易得 \(len=r-l+1\)

从左往右弄个\(2^{\log_2(len)}\)的区间，再从右往左弄一个即可。

代码：

P3865 【模板】ST表

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;

const int N = 2e5 + 10, M = 20;
int n,m;
int f[N][M];
int w[N];

void init()
{
    for(int j = 0; j < M; j ++ )
        for (int i = 1; i + (1 << j) - 1 <= n; i ++ )//不能越界
            if(!j) f[i][j] = w[i];
            else f[i][j] = max(f[i][j - 1],f[i + (1 << j - 1)][j - 1]);
}

int query(int l,int r)
{
    int len = r - l + 1;
    int k = log(len) / log(2);
    return max(f[l][k],f[r - (1 << k) + 1][k]);
}

int main()
{
    scanf("%d%d", &n,&m);
    for (int i = 1; i <= n; i ++ )
        scanf("%d", &w[i]);
    init();    
    while(m -- )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n",query(l,r));
    }
    return 0;
}

习题

1.P2880 [USACO07JAN] Balanced Lineup G

求区间极差，先用 ST 表算出区间内的最小值 \(minn\) 和最大值 \(maxx\),然后将两数相减即可

2.P1890 gcd区间

直接套模板算出来每个区间的最大公约数就行，因为 \(\gcd\) 也具有同样的性质