NOIP经典基础模板总结
date: 20180820
spj: 距离NOIP还有81天
目录
STL模板:
priority_queue 的用法:重载<,struct cmp
queue 的用法
stack 的用法
vector的用法
map和set的用法
* 遍历容器中得所有元素
dequeue双端队列的用法
基础数论模板:
gcd
ex_gcd
求phi():筛选法、定义法
筛选法求质数
判断质数的一般方法
快速幂
矩阵快速幂
求逆元的方法(递推式、快速幂、ex_gcd)
卢卡斯定理的实现
组合数朴素公式
组合数递推式(杨辉三角)
组合数取模
二项式定理
n的正约数个数(唯一分解定理的推导)
ST表
裴蜀定理
高精度计算+-*
*二项式反演
*离散概率
图论模板:
floyd求最短路求最小环、图的传递闭包
spfa求最短路、dijkstra堆优化求最短路
kosaraju算法求强联通分量
tarjan求强联通分量
最小生成树
倍增LCA、tarjan LCA
并查集(启发式)
前向星存图
KM求最优匹配、匈牙利算法求最大匹配
FF算法求最大流
*最小费用最大流
树上Hash
数据结构模板:
树状数组模板(区间最大最小和)
线段树模板(区间最大最小和)
字典树(STL实现)
实数二分,整数二分答案
*线性基
字符串模板:
字符串哈希Hash(字符串必备)
*KMP算法初步
*AC自动机
说明:打*的模板未学习,历年NOIP范围内并未涉及,在本blog中不展开讲解(放代码)
正文
STL模板:
priority_queue 的用法:重载<,struct cmp
定义:
/*下面两种优先队列的定义是等价的*/ priority_queue<int> q; priority_queue<int,vector<int>,less<int> > q;//后面有一个空格 /*这一种写法与上面不等价,恰好相反*/ priority_queue<int,vectot<int>,greater<int> > q;
重载小于号:
struct rec{ int x,y; bool operator < (rec other){ if (x!=other.x) return x<other.x; else return y<other.y; } };
struct cmp
struct cmp{ bool operator () (rec a,b){ if (a.x!=b.x) return a.x<b.x; else return a.y<b.y; } }; priority_queue<rec,vector<rec>,cmp>q;
基本操作:
.top() 访问堆顶元素
.push() 插入一个新元素
.pop() 删除堆顶元素
.empty() 是否为空
.size() 堆中元素个数
queue 的用法
单端队列
.empty() 判断队列q是否为空
.size() 访问队列q中的元素个数
.push() 会将一个元素a置入队列q中
.front() 返回队列q内的第一个元素
.back() 会返回队列q中最后一个元素
.pop() 会从队列q中移除第一个元素。
stack 的用法
.empty() 堆栈为空则返回真
.pop() 移除栈顶元素(不会返回栈顶元素的值)
.push() 在栈顶增加元素
.size() 返回栈中元素数目
.top() 返回栈顶元素
vector的用法
定义:vector<int>a;
用法:
.back(); 返回a的最后一个元素 .front(); 返回a的第一个元素 .push_back(); 插入一个元素 a[i]; 返回a的第i个元素,当且仅当a[i]存在 .erase(a.begin()+1,a.begin()+3);
删除a中第1个(从第0个算起)到第2个元素也就是说删除的元素从a.begin()+1算起(包括它)一直到a.begin()+3(不包括它) .pop_back(); 删除a向量的最后一个元素 .clear(); 清空a中的元素 .empty(); 判断a是否为空,空则返回ture,不空则返回false .swap(b); b为向量,将a中的元素和b中的元素进行整体性交换 .find(a.begin(),a.end(),10);
在a中的从a.begin()(包括它)到a.end()(不包括它)的元素中查找10,若存在返回其在向量中的位置
遍历: for(vector<int>::iterator it=b.begin();it!=b.end();it++) *it就是元素值
map和set的用法
定义:
map<int,int>mp;//定义一个map set<int>stt;//定义一个set
用法:
map
begin() 返回指向map头部的迭代器 clear() 删除所有元素 count() 返回指定元素出现的次数 empty() 如果map为空则返回true end() 返回指向map末尾的迭代器 erase() 删除一个元素 find() 查找一个元素 insert() 插入元素 lower_bound() 返回键值>=给定元素的第一个位置
upper_bound() 返回键值>给定元素的第一个位置 size() 返回map中元素的个数
set
begin() 返回指向第一个元素的迭代器
clear() 清除所有元素
count() 返回某个值元素的个数
empty() 如果集合为空,返回true
end() 返回指向最后一个元素的迭代器
erase() 删除集合中的元素
find() 返回一个指向被查找到元素的迭代器
insert() 在集合中插入元素
lower_bound() 返回指向大于(或等于)某值的第一个元素的迭代器
upper_bound() 返回大于某个值元素的迭代器
size() 集合中元素的数目
* 遍历容器中得所有元素
//这里以vector为例 for (vector<int>::iterator it=a.begin();it!=a.end();it++)
printf("%d ",*it);
dequeue双端队列的用法
.size() 返回容器中实际数据的个数。
.pop_back() 删除最后一个数据。
.pop_front() 删除头部数据。
.erase(pos) 删除pos位置的数据,传回下一个数据的位置。
.erase(beg,end) 删除[beg,end)区间的数据,传回下一个数据的位置。
.front() 传回地一个数据。
.empty() 判断容器是否为空。
.end() 指向迭代器中的最后一个数据地址。
.back() 传回最后一个数据,不检查这个数据是否存在。
.begin() 传回迭代器重的可一个数据。
.clear() 移除容器中所有数据。
基础数论模板:
gcd
求a,b的最大公约数gcd(a,b) int simple_gcd(int a,int b) { if (b==0) return a; return simple_gcd(b,a%b); // 代码更短: return (!b)?a:simple_gcd(b,a%b); }
ex_gcd
/* 求ax+by=gcd(a,b)的正整数解一组 证明: 易证明 a-[a/b]*b=a%b 由朴素gcd定理可知: gcd(a,b)=gcd(b,a%b) ax1+by1=bx2+(a%b)y2=gcd(a,b) ax1+by1=bx2+( a-[a/b]*b)y2 解之得:x1=y2,y1=x2-[a/b]*y2; */ int ex_gcd(int a,int b,int &x,int &y) { if (b==0) { x=1;y=0; return a; } int r=ex_gcd(b,a%b,x,y); int t=x;x=y;y=t-a/b*y; return r; }
判断质数的一般方法
bool checkprime(int x) { for (int i=2;i<=ceil(sqrt(x));i++) if (!(x%i)) return false; return true; }
筛选法求质数
void getprime(int n) { bool prime[MAXN+1]; memset(prime,true,sizeof(prime)); vector<int>a;a.clear(); for (int i=2;i<=n;i++) { if (prime[i]==false) continue; a.push_back(i); for (int j=i+i;j<=n;j+=i) prime[j]=false; } for (int i=0;i<a.size();i++) printf("%d ",a[i]);//求出1-n所有质数 }
米勒罗宾判断质数:
int pow(int x,int n,int mo) { int ans=1; while (n) { if (n&1) ans=ans*x%mo; x=x*x%mo; n>>=1; } return ans; } int is_prime(int x) { if (x==0||x==1) return -1; if (x==2) return 1; for (int i=1;i<=MAXT;i++) { int m=rand()%(x-1)+1; if (pow(m,x-1,x)!=1) return 0; } return 1; }
求phi():筛选法、定义法
定义法:
void getprime(int n) { memset(prime,true,sizeof(prime));a.clear(); for (int i=2;i<=n;i++) { if (prime[i]==false) continue; a.push_back(i); for (int j=i+i;j<=n;j+=i) prime[j]=false; } } int phi(int x) { getprime(x); int p=0,ph=x; for (;;){ int nowprime=a[p]; if (nowprime>x||p==a.size()-1) break; if (x%nowprime==0) ph=ph*(nowprime-1)/nowprime; p++; } return ph; }
筛选法:
void getphi(int x) { memset(phi,0,sizeof(phi)); phi[1]=1; for (int i=2;i<=x;i++) if (phi[i]==0) { for (int j=i;j<=x;j+=i){ if (phi[j]==0) phi[j]=j; phi[j]=phi[j]/i*(i-1); } } }
快速幂
递归式写法
const int mo=100000007; int pow(int x,int n) { if (n==0) return 1; if (n==1) return x; int t=pow(x,n/2)%mo; t=t*t%mo; if (n%2) t=t*x%mo; return t; }
非递归式写法(加快乘)
//wrong code fixed by lukelin int mul(int x,int n,int p){ int ans=0; for (;n;n>>=1,x=(x<<1)%p) if (n&1) ans=(ans+x)%p; return ans; } int fpow(int x,int n,int p){ int ans=1; for (;n;n>>=1,x=x*x%p) if (n&1) ans=(ans*x)%p; return ans; }
矩阵快速幂
const int mo=1e9+7; const int MatixWide=2; struct Matix{ int m[MatixWide+1][MatixWide+1]; Matix operator * (const Matix &t) const { Matix ans; memset(ans.m,0,sizeof(ans.m)); for (int i=1;i<=MatixWide;i++) for (int j=1;j<=MatixWide;j++) { int sum=0; for (int k=1;k<=MatixWide;k++) sum=(sum+m[i][k]*t.m[k][j]%mo)%mo; ans.m[i][j]=sum; } return ans; } }; Matix pow(Matix x,int n) { Matix ans; memset(ans.m,0,sizeof(ans.m)); ans.m[1][1]=ans.m[2][1]=1;n--; while (n) { if (n&1) ans=ans*x; x=x*x; n>>=1; } return ans; }
求逆元的方法(递推式、快速幂、ex_gcd)
快速幂求逆元:
/* 基于费马小定理pow(a,p-2)%p 就是a在mod p意义下的逆元 */ int pow(int x,int n,int m) { if (n==0) return 1; if (n==1) return x; int t=pow(x,n/2,m)%m; t=t*t%m; if (n%2) t=t*x%m; return t; } int inv(int x,int m) { return pow(x,m-2,m)%m; }
扩展欧几里得求逆元
/* 求ax=1(mod p) 就是求ax%p=1,所以ax ax=kp+1,就是ax-kp=1, 当p为质数的时候gcd(a,-p)=1,求此时x的值就是逆元 注意模到正数就行 */ int ex_gcd(int a,int b,int &x,int &y) { if (b==0) { x=1;y=0; return a; } int r=ex_gcd(b,a%b,x,y); int t=x;x=y;y=t-a/b*y; return r; } int inv(int a,int m) { int x,y; int g=ex_gcd(a,m,x,y); return (x+m)%m; }
筛选法求逆元
/* inv[i]=(p-p/i)*inv[p%i]%p 证明: 设t=p/i,k=p%i 那么 t*i+k=0(mod p) 同时除以i*k得: -t/k=1/i 所以 1/i=-t*1/k=-p/i*inv[p%i] 所以 把1/i(inv[i])调成正数为 inv[i]=(p-p/i)*inv[p%i]%p */ void getinv(int x,int p) { memset(inv,0,sizeof(inv)); inv[1]=1; for (int i=2;i<=x;i++) inv[i]=(long long)(p-p/i)%p*inv[p%i]%p; }
组合数朴素公式
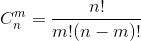
其中 n!=1*2*...*n,特别的,0!=1;
卢卡斯定理的实现
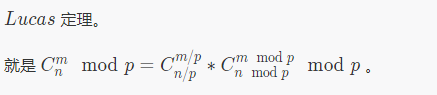
long long lucas(int m,int n) { if(n<m) return 0; else if(n<p) return s[n]*inv[m]*inv[n-m]%p; else return lucas(m/p,n/p)*lucas(m%p,n%p)%p; } void getready() { inv[0]=inv[1]=s[0]=s[1]=1; for(int i=2;i<=n;i++) { s[i]=s[i-1]*i%p; inv[i]=(p-p/i)*inv[p%i]%p; } for(int i=2;i<=n;i++) inv[i]=inv[i-1]*inv[i]%p; }
组合数递推式(杨辉三角)
for (int i=0;i<=n;i++) c[i][i]=c[i][0]=1; for (int i=1;i<=n;i++) for (int j=1;j<i;j++) c[i][j]=c[i-1][j-1]+c[i-1][j];
组合数取模
上至lucas定理或者暴力乘以inv(m!)和inv((n-m)!)公式法求解
二项式定理

n的正约数个数(唯一分解定理的推导)
/* 唯一分解定理:n=p1^a1+p2^a2+p3^a3+...+pk^ak 正约数个数为(a1+1)(a2+1)...(ak+1)个 如果是质数那么约数一定是2 特判1的约数为1 */ int getnum(int x) { getprime(x); if (x==0||x==1) return 1; //其实0的约数没有意义 if (prime[x]) return 2; int p=0,ans=1,cnt; for (;;){ int nowprime=a[p]; if (nowprime>x||p==a.size()-1) break; cnt=1; while (x%nowprime==0) cnt++,x/=nowprime; ans*=cnt; p++; } return ans; }
ST表
# include <bits/stdc++.h> /* ST表:倍增思想 MAX[i][j]第i个数后面2^j-1个数(含i是2^j)最大值 初始化:MAX[i][0]=a[i] dp:MAX[i][j]=max(MAX[i][j-1],MAX[i+2^(j-1)][j-1]) 求值令k=log2(r-l+1) ans=max(MAX[l][k],MAX[r+1-2^k][k]) */ using namespace std; const int MAXN=100005; int a[MAXN],MAX[MAXN][21],n,m; inline int read() { int X=0,w=0; char c=0; while(c<'0'||c>'9') {w|=c=='-';c=getchar();} while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar(); return w?-X:X; } void init() { memset(MAX,0,sizeof(MAX)); for (int i=1;i<=n;i++) MAX[i][0]=a[i]; for (int j=1;j<=21;j++) for (int i=1;i+(1<<j)-1<=n;i++) MAX[i][j]=max(MAX[i][j-1],MAX[i+(1<<(j-1))][j-1]); } int query(int l,int r) { int k=log2(r-l+1); return max(MAX[l][k],MAX[r-(1<<k)+1][k]); } int main() { n=read(),m=read(); for (int i=1;i<=n;i++) a[i]=read(); init(); int l,r; while (m) { l=read(),r=read(); printf("%d\n",query(l,r)); m--; } return 0; }
裴蜀定理
ax+by=c(x ∈N* ,y∈N*) 有正整数解的充要条件:gcd(a,b)∣c
设 s=gcd(a,b) ,显然s∣a ,并且s∣b
又因为x,y∈Z∗
所以s∣ax,s∣by
显然要使得之前的式子成立,则必须满足 c 是 a 和 b 的公约数的倍数
又因为 x 和 y 是正整数
所以 c 必然是 a,b 最大公约数的倍数。
因此,证得该定理成立
所以 对于给定a,b的f(x)=ax+by(x ∈N* ,y∈N*)最小值为c=gcd(a,b)
扩展到多元就是累计的gcd{ai} 就是最小值。
# include <bits/stdc++.h> using namespace std; int gcd(int a,int b) { return b==0?a:gcd(b,a%b); } int main() { int n,ans=0,a; scanf("%d",&n); while (n--) { scanf("%d",&a); a=(a>0)?a:-a; ans=gcd(ans,a); } printf("%d\n",ans); return 0; }
高精度计算
/* Hint:支持正大整数a,b加法,减法(a>b), 支持大整数除以long long范围的实数 支持long long 转化为大整数 大整数转化为 unsigned long long 比大小 < : a<b true : false; > : a>b true :false <=:a<=b true:false >=a>=b true :false != a!=b true :false == a==b true :false 类型是lint ,输入值为lint,输出值为lint 支持位数为L=100005 */ # include<bits/stdc++.h> # define LL long long # define Rint register int using namespace std; const int L=100005; char s[L]; struct lint{ int len,num[L]; inline lint operator + (const lint &t) const{ lint ans; memset(ans.num,0,sizeof(ans.num)); if (len>t.len) ans.len=len; else ans.len=t.len; for (Rint i=1;i<=ans.len;i++) { ans.num[i]+=num[i]+t.num[i]; ans.num[i+1]+=ans.num[i]/10; ans.num[i]%=10; } if (ans.num[ans.len+1]>0) ans.len++; return ans; } inline lint operator * (const lint &t) const{ lint ans; memset(ans.num,0,sizeof(ans.num)); for (Rint i=1;i<=len;i++) for (Rint j=1;j<=t.len;j++) ans.num[i+j-1]+=num[i]*t.num[j]; for (Rint i=1;i<=len+t.len;i++) { ans.num[i+1]+=ans.num[i]/10; ans.num[i]%=10; } if (ans.num[len+t.len]>0) ans.len=len+t.len; else ans.len=len+t.len-1; return ans; } inline lint operator - (const lint &t) const { int nm=0,rs=0; lint ans; for (Rint i=1;i<=len+1;i++) { nm=num[i]-t.num[i]-rs; rs=0; while (nm<0) rs++,nm+=10; ans.num[i]=nm; } int i; for (i=len;i>=2;i--) if (ans.num[i]>0) break; ans.len=i; return ans; } inline lint operator / (const int &x) { lint a; a.len=len; int rest=0; for (int i=len;i>=1;i--){ rest=rest*10+num[i]; a.num[i]=rest/x; rest%=x; } while (!a.num[a.len]&&a.len>1) a.len--; return a; } inline lint read() { lint a; memset(a.num,0,sizeof(a.num)); scanf("%s",s); a.len=strlen(s); for (Rint i=1;i<=a.len;i++) a.num[i]=s[a.len-i]-'0'; return a; } inline int cmp(lint a,lint b) { if (a.len<b.len) return 1; else if (a.len>b.len) return -1; for (Rint i=a.len;i>=1;i--) if (a.num[i]>b.num[i]) return -1; else if (a.num[i]<b.num[i]) return 1; return 0; } inline bool operator < (const lint &t) const{ if (len>t.len) return 0; else if (len<t.len) return 1; for (Rint i=len;i>=1;i--) if (num[i]<t.num[i]) return 1; else if (num[i]>t.num[i]) return 0; return 0; } inline bool operator <= (const lint &t) const{ if (len>t.len) return 0; else if (len<t.len) return 1; for (Rint i=len;i>=1;i--) if (num[i]<t.num[i]) return 1; else if (num[i]>t.num[i]) return 0; return 1; } inline bool operator > (const lint &t) const{ if (len>t.len) return 1; else if (len<t.len) return 0; for (Rint i=len;i>=1;i--) if (num[i]<t.num[i]) return 0; else if (num[i]>t.num[i]) return 1; return 0; } inline bool operator >= (const lint &t) const{ if (len>t.len) return 1; else if (len<t.len) return 0; for (Rint i=len;i>=1;i--) if (num[i]<t.num[i]) return 0; else if (num[i]>t.num[i]) return 1; return 1; } inline bool operator ==(const lint &t) const{ if (len>t.len||len<t.len) return 0; for (Rint i=len;i>=1;i--) if (num[i]!=t.num[i]) return 0; return 1; } inline bool operator !=(const lint &t) const{ if (len>t.len||len<t.len) return 1; for (Rint i=len;i>=1;i--) if (num[i]!=t.num[i]) return 1; return 0; } inline void swap(lint &a,lint &b) { lint t=a; a=b; b=t; } inline void print(lint x) { for (Rint i=x.len;i>=1;i--) printf("%d",x.num[i]); putchar('\n'); } inline lint change(LL x) { lint a; memset(a.num,0,sizeof(a.num)); if (x==0) { a.num[1]=0; a.len=1; return a;} a.len=0; while (x>0) a.num[++a.len]=x%10,x/=10; return a; } inline unsigned LL rechange(lint x) { unsigned LL a=0ll; for (Rint i=x.len;i>=1;i--) a=a*10+x.num[i]; return a; } }R; void work1() { lint a=R.read(),b=R.read(),c; printf("a-b="); if (a<b) { R.swap(a,b); printf("-");} R.print(a-b); c=a+b; printf("a+b="); R.print(c); c=a*b; printf("a*b="); R.print(c); printf("a<b = "); printf((a<b)?"Yes\n":"No\n"); printf("a<=b = "); printf((a<=b)?"Yes\n":"No\n"); printf("a>b = "); printf((a>b)?"Yes\n":"No\n"); printf("a>=b = "); printf((a>=b)?"Yes\n":"No\n"); printf("a==b = "); printf((a==b)?"Yes\n":"No\n"); printf("a!=b = "); printf((a!=b)?"Yes\n":"No\n"); } void work2() { unsigned LL a,b; scanf("%lld",&a); lint u=R.change(a); b=R.rechange(u); printf("%lld\n",b); } int main() { work1(); work2(); return 0; }
离散化:
void lisanhua(int *d,int len) { tmp.clear(); for (int i=1;i<=len;i++) tmp.push_back(d[i]); sort(tmp.begin(),tmp.end()); vector<int>::iterator it=unique(tmp.begin(),tmp.end()); for (int i=1;i<=len;i++) d[i]=lower_bound(tmp.begin(),it,d[i])-tmp.begin()+1; }
图论模板:
floyd求最短路求最小环、图的传递闭包
最短路:
# include <bits/stdc++.h> # define Rint register int using namespace std; const int MAXN=105; int mp[MAXN][MAXN]; int main() { int n,m,s; scanf("%d%d%d",&n,&m,&s); for (Rint i=1;i<=MAXN;i++) for (Rint j=1;j<=MAXN;j++) if (i!=j) mp[i][j]=INT_MAX/3; int INF=mp[1][2]; int u,v,w; for (Rint i=1;i<=m;i++) { scanf("%d%d%d",&u,&v,&w); mp[u][v]=min(w,mp[u][v]); } for (Rint k=1;k<=n;k++) for (Rint i=1;i<=n;i++) for (Rint j=1;j<=n;j++) if (k!=i&&i!=j&&j!=k) mp[i][j]=min(mp[i][j],mp[i][k]+mp[k][j]); for (Rint i=1;i<=n;i++) if (mp[s][i]==INF) printf("2147483647 "); else printf("%d ",mp[s][i]); printf("\n");return 0; }
最小环
# include <bits/stdc++.h> # define Rint register int using namespace std; const int MAXN=105; int mp[MAXN][MAXN],dist[MAXN][MAXN]; int main() { int n,m,s; scanf("%d%d%d",&n,&m,&s); for (Rint i=1;i<=MAXN;i++) for (Rint j=1;j<=MAXN;j++) if (i!=j) dist[i][j]=mp[i][j]=INT_MAX/3; int INF=mp[1][2]; int u,v,w; for (Rint i=1;i<=m;i++) { scanf("%d%d%d",&u,&v,&w); mp[u][v]=mp[v][u]=dist[u][v]=dist[v][u]=min(w,mp[u][v]); } int ans=INT_MAX; for (Rint k=1;k<=n;k++) { for (Rint i=1;i<=k-1;i++) for (Rint j=i+1;j<=k-1;j++) ans=min(ans,dist[i][j]+mp[k][i]+mp[j][k]); for (Rint i=1;i<=n;i++) for (Rint j=1;j<=n;j++) dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j]); } printf("%d\n",ans); return 0; }
传递闭包
# include <bits/stdc++.h> # define Rint register int using namespace std; bool mp[101][101]; int n,m; int main() { scanf("%d%d",&n,&m); memset(mp,false,sizeof(mp)); for (int i=1;i<=n;i++) mp[i][i]=true; int u,v; for (int i=1;i<=m;i++) scanf("%d%d",&u,&v),mp[u][v]=true; for (Rint k=1;k<=n;k++) for (Rint i=1;i<=n;i++) for (Rint j=1;j<=n;j++) mp[i][j]=mp[i][j]|(mp[i][k]&&mp[k][j]); for (Rint i=1;i<=n;i++) { for (Rint j=1;j<=n;j++) if (mp[i][j]) printf("Y "); else printf("N "); printf("\n"); } return 0; }
spfa求最短路、dijkstra堆优化求最短路
spfa求最短路
# include <bits/stdc++.h> using namespace std; queue<int>q; struct rec { int pre,to,w; }; const int MAXN=10005,MAXM=500005,inf=2147483647; int N,M,S,tot=0; int head[MAXN],d[MAXN]; rec a[MAXM]; void adde(int u,int v,int w) { a[++tot].pre=head[u]; a[tot].to=v; a[tot].w=w; head[u]=tot; } void spfa(int s) { for (int i=1;i<=N;i++) d[i]=inf; d[s]=0; q.push(s); while (!q.empty()) { int v0=q.front();q.pop(); for (int i=head[v0];i!=0;i=a[i].pre){ if (d[v0]<d[a[i].to]-a[i].w) { d[a[i].to]=d[v0]+a[i].w; q.push(a[i].to); } } } } int main() { scanf("%d%d%d",&N,&M,&S); int u,v,w; for (int i=1;i<=M;i++){ scanf("%d%d%d",&u,&v,&w); adde(u,v,w); } spfa(S); for (int i=1;i<=N;i++) printf("%d ",d[i]); printf("\n"); return 0; }
dijktra求最短路
/* 思想是每次找与当前便利点u最近的元素用它来更新子节点 */ #include <bits/stdc++.h> using namespace std; const int MAXM=500005,MAXN=10005; int head[MAXN],d[MAXN],n,m,s,tot=0,INF; bool vis[MAXN]; struct record{ int pre,to,w; }a[MAXM]; void adde(int u,int v,int w) { a[++tot].pre=head[u]; a[tot].to=v; a[tot].w=w; head[u]=tot; } struct rec{ int id,lenth; bool operator < (const rec a)const{ if (lenth!=a.lenth) return lenth>a.lenth; else return id>a.id; } }; priority_queue<rec>q; void dijkstra(int s) { memset(vis,false,sizeof(vis)); memset(d,127,sizeof(d));INF=d[0];d[s]=0; rec Node; Node.id=s; Node.lenth=0; q.push(Node); while (! q.empty()){ rec Node=q.top(); q.pop(); int u=Node.id; if (vis[u]==true) continue; vis[u]=true; for (int i=head[u];i!=0;i=a[i].pre){ int v=a[i].to; if (d[v]-a[i].w>d[u]) { d[v]=a[i].w+d[u]; rec N; N.id=v;N.lenth=d[v]; q.push(N); } } } } int main() { scanf("%d%d%d",&n,&m,&s); for (int i=1;i<=m;i++) { int u,v,w; scanf("%d%d%d",&u,&v,&w); adde(u,v,w); } dijkstra(s); for (int i=1;i<=n;i++) if (d[i]==INF) printf("2147483647 "); else printf("%d ",d[i]); return 0; }
求次短路
# include <iostream> # include <cstdio> # include <queue> # include <algorithm> # define int long long using namespace std; const int MAXN=5005; const int MAXM=2*100005; struct A{ int pre,to,w;}a[MAXM]; struct B{ int u,v,w;}; vector<B>E; int head[MAXN],d1[MAXN],d2[MAXN],tot=0,n,m; bool vis[MAXN]; inline int read() { int X=0,w=0;char c=0; while (!(c>='0'&&c<='9')) w|=c=='-',c=getchar(); while (c>='0'&&c<='9') X=(X<<1)+(X<<3)+(c^48),c=getchar(); return w?-X:X; } inline void write(int x) { if (x<0) { putchar('-');x=-x;} if (x>9) write(x/10); putchar(x%10+'0'); } inline void writeln(int x){write(x);putchar('\n');} inline void adde(int u,int v,int w) { a[++tot].pre=head[u]; a[tot].to=v; a[tot].w=w; head[u]=tot; } struct node{ int id,val;}; struct cmp{ bool operator () (node a,node b) const{ return a.val>b.val; } }; priority_queue<node,vector<node>,cmp>q; void dijkstra(int s,int *dist) { for(int i=1;i<=n;i++) dist[i]=0x7f7f7f7f7f,vis[i]=false; dist[s]=0; node Tmp; Tmp.id=s,Tmp.val=0; q.push(Tmp); while (!q.empty()) { node u=q.top();q.pop(); if (vis[u.id]) continue; vis[u.id]=true; for (int i=head[u.id];i;i=a[i].pre) { int v=a[i].to; if (dist[v]-a[i].w>dist[u.id]) { dist[v]=a[i].w+dist[u.id]; Tmp.id=v,Tmp.val=dist[v]; q.push(Tmp); } } } } signed main() { n=read();m=read(); for (int i=1;i<=m;i++) { int u=read(),v=read(),w=read(); B Tmp1,Tmp2; Tmp1.u=u;Tmp1.v=v;Tmp1.w=w; Tmp2.u=v;Tmp2.v=u;Tmp2.w=w; E.push_back(Tmp1); E.push_back(Tmp2); adde(u,v,w); adde(v,u,w); } dijkstra(1,d1); dijkstra(n,d2); int shortest=d1[n]; int Ans=0x7f7f7f7f7f; for (int i=0;i<E.size();i++) if (d1[E[i].u]+d2[E[i].v]+E[i].w!=shortest) Ans=min(Ans,d1[E[i].u]+d2[E[i].v]+E[i].w); writeln(Ans); return 0; }
kosaraju算法求强联通分量
/* https://www.cnblogs.com/ljc20020730/p/9359951.html 反图:设G为原图,F图为反图。 step1:对G遍历记录每个点的退出顺序dfn[] 对于下面这个图遍历序列为1 2 3 5 (5 3 2 )1 3(4 1) 括号括起来的是返回值 dfn=5 3 2 4 1 step2:对反图F 按照dfn的反序对反图进行dfs遍历 访问过程:1 4 (return)2 5 3 (return) F图如下: 得出两个强联通分量就是14 ; 2 5 3; 在最小环处理的问题上要注意两个问题 1.图的强联通问题:必须保证图的联通性如果不行,那么反复dfs知道找到所有点为止 2.单个的点不是环及dfs2中得出cnt=1的情况要舍去 */ # include <cstdio> # include <cstring> # include <iostream> using namespace std; struct rec{ int pre,to; }; const int MAXN=1000005; int n,m,tot1=0,tot2=0; int dfn[MAXN],head1[MAXN],head2[MAXN]; bool vis[MAXN]; rec a[MAXN],b[MAXN]; int adde1(int u,int v) //正图前向星 { tot1++; a[tot1].pre=head1[u]; a[tot1].to=v; head1[u]=tot1; } int adde2(int u,int v)//反图前向星 { tot2++; b[tot2].pre=head2[u]; b[tot2].to=v; head2[u]=tot2; } int dfs1(int u) //求dfn序 { vis[u]=true; for (int i=head1[u];i!=0;i=a[i].pre) { int v=a[i].to; if (vis[v]==true) continue; dfs1(v); } dfn[++dfn[0]]=u; } int dfs2(int u) //求环 { vis[u]=true; for (int i=head2[u];i!=0;i=b[i].pre) { int v=b[i].to; if (vis[v]==true) continue; dfs2(v); } printf("%d ",u); } int main() { scanf("%d%d",&n,&m); for (int i=1;i<=m;i++) { int u,v; scanf("%d%d",&u,&v); adde1(u,v); adde2(v,u);//正图A,反图B; } memset(dfn,0,sizeof(dfn)); memset(vis,false,sizeof(vis)); for (int i=1;i<=n;i++) if (vis[i]==false) dfs1(i); //得出dfn /* printf("*****************************************************\n"); printf("调试输出dfn[]: "); for (int i=1;i<=dfn[0];i++) printf("%d ",dfn[i]); for (int i=1;i<=first[0];i++) printf("%d ",first[i]); printf("\n"); printf("*****************************************************\n"); */ memset(vis,false,sizeof(vis)); int cnt=0; for (int i=dfn[0];i>0;i--) //反序搞一搞求强联通块 { if (vis[dfn[i]]==true) continue; cnt++; printf("强联通块# %d :",cnt); dfs2(dfn[i]); printf("\n"); } return 0; }
tarjan求强联通分量
# include <bits/stdc++.h> using namespace std; const int MAXN=1000005,MAXM=1000005; bool ins[MAXN]; int low[MAXN],dfn[MAXN],head[MAXN],tot=0,tt=0,n,m; struct rec{ int pre,to; }a[MAXM]; stack<int>s; void adde(int u,int v) { a[++tot].pre=head[u]; a[tot].to=v; head[u]=tot; } void trajan(int u) { tt++; low[u]=dfn[u]=tt; s.push(u); ins[u]=true; for (int i=head[u];i;i=a[i].pre) { int v=a[i].to; if (! dfn[v]) { trajan(v); low[u]=min(low[u],low[v]); } else if (ins[v]) low[u]=min(low[u],dfn[v]); } if (dfn[u]==low[u]) { while (true) { int v=s.top();s.pop();ins[v]=false; printf("%d ",v); if (u==v) break; } printf("\n"); } } int main() { scanf("%d%d",&n,&m); int u,v; for (int i=1;i<=m;i++) scanf("%d%d",&u,&v),adde(u,v); memset(ins,false,sizeof(ins)); memset(dfn,0,sizeof(dfn)); for (int i=1;i<=n;i++) if (!dfn[i]) trajan(i); return 0; }
最小生成树
# include<bits/stdc++.h> using namespace std; const int MAXN=5005,MAXM=2000005; struct rec{ int u,v,w; }; int tot=0; rec a[MAXM]; int f[MAXN]; int n,m; bool cmp(rec x,rec y) { return x.w<y.w; } int father(int x) { if (f[x]==x) return x; f[x]=father(f[x]); return f[x]; } void kruskal() { sort(a+1,a+1+tot,cmp); for (int i=1;i<=n;i++) f[i]=i; int cnt=0,ans=0; for (int i=1;i<=m;i++){ int fx=father(a[i].u); int fy=father(a[i].v); if (fx==fy) continue; f[fx]=fy; cnt++; ans+=a[i].w; if (cnt==n-1) break; } if (cnt==n-1) printf("%d\n",ans); else printf("无解"); } int main() { scanf("%d%d",&n,&m); tot=0; for (int i=1;i<=m;i++) { int u,v,w; scanf("%d%d%d",&u,&v,&w); a[++tot].u=u; a[tot].v=v; a[tot].w=w; } kruskal(); return 0; }
倍增LCA、tarjan LCA
倍增lca
# include <iostream> # include <cstdio> # include <cstring> using namespace std; struct rec{ int pre,to; }; int tot,H,n,m,s; const int MAXN=2*500005; int head[MAXN],dep[MAXN],g[MAXN][30]; bool vis[MAXN]; rec a[MAXN]; inline int read() { int X=0,w=0; char c=0; while(c<'0'||c>'9') {w|=c=='-';c=getchar();} while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar(); return w?-X:X; } inline void adde(int u,int v) { a[++tot].pre=head[u]; a[tot].to=v; head[u]=tot; } inline void dfs(int u,int depth) { vis[u]=true; dep[u]=depth; for (register int i=head[u];i!=0;i=a[i].pre) { int v=a[i].to; if (vis[v]) continue; g[v][0]=u;dfs(v,depth+1); } } inline void init() { memset(g,0,sizeof(g)); memset(vis,false,sizeof(vis)); dfs(s,1); g[s][0]=s; for (register int j=1;j<=21;j++) for (register int i=1;i<=n;i++) g[i][j]=g[g[i][j-1]][j-1]; } inline int LCA(int u,int v) { if (dep[u]<dep[v]) swap(u,v); for (register int i=21;i>=0;i--) if (dep[g[u][i]]>=dep[v]) u=g[u][i]; if (u==v) return u; for (register int i=21;i>=0;i--) if (g[u][i]!=g[v][i]) u=g[u][i],v=g[v][i]; return g[u][0]; } int main() { n=read();m=read();s=read(); int u,v; for (register int i=1;i<=n-1;i++) {u=read();v=read(); adde(u,v);adde(v,u);} init(); while (m--){ u=read();v=read(); printf("%d\n",LCA(u,v)); } return 0; }
tarjanLCA
/* 1.任选一个点为根节点,从根节点开始。 2.遍历该点u所有子节点v,并标记这些子节点v已被访问过。 3.若是v还有子节点,返回2,否则下一步。 4.合并v到u上。 5.寻找与当前点u有询问关系的点v。 6.若是v已经被访问过了,则可以确认u和v的最近公共祖先为v被合并到的父亲节点a。 */ # include <iostream> # include <cstdio> # include <cstring> # include <algorithm> using namespace std; const int MAXN=1000005,MAXM=1000005; struct rec{ int pre,to,ans; }; int head[MAXN],qhead[MAXN],f[MAXN]; bool vis[MAXN]; rec a[MAXM],qes[MAXM]; int n,m,q,tot=0; void adde(int u,int v) { tot++; a[tot].to=v; a[tot].pre=head[u]; head[u]=tot; } void qadde(int u,int v,int x) { qes[x].to=v; qes[x].pre=qhead[u]; qhead[u]=x; } int father(int x) { if (f[x]==x) return x; f[x]=father(f[x]); return f[x]; } void calc(int x,int y) { int fx=father(x); int fy=father(y); f[fy]=fx; } void tarjan(int u) { vis[u]=true; for(int i=head[u];i!=0;i=a[i].pre) { int v=a[i].to; if (vis[v]==false) { tarjan(v); calc(u,v); } } for (int i=qhead[u];i!=0;i=qes[i].pre) { int v=qes[i].to; if (vis[v]==false) continue; qes[i].ans=father(v); if (i%2==0) qes[i-1].ans=qes[i].ans; else qes[i+1].ans=qes[i].ans; } } int main() { int n,m,s; scanf("%d%d%d",&n,&m,&s); memset(f,0,sizeof(f)); memset(a,0,sizeof(a)); for (int i=1;i<=n-1;i++) { int u,v; scanf("%d%d",&u,&v); adde(u,v);adde(v,u); f[i]=i; } f[n]=n; for (int i=1;i<=m;i++){ int u,v; scanf("%d%d",&u,&v); qadde(u,v,2*i-1);qadde(v,u,2*i); } memset(vis,false,sizeof(vis)); tarjan(s); for (int i=1;i<=m;i++) printf("%d\n",qes[2*i].ans); return 0; }
并查集(启发式)
# include <bits/stdc++.h> using namespace std; const int MAXN=10005; int fa[MAXN]; int n,m; int father(int x) { if (fa[x]==x) return x; fa[x]=father(fa[x]); return fa[x]; } void calc(int x,int y) { int fx=father(x),fy=father(y); fa[fx]=fy; } bool check(int x,int y) { int fx=father(x),fy=father(y); if (fx==fy) return true; else return false; } int main() { scanf("%d%d",&n,&m); for (int i=1;i<=n;i++) fa[i]=i; int u,v,ch; for (int i=1;i<=m;i++) { scanf("%d%d%d",&ch,&u,&v); if (ch==1) calc(u,v); else { if (check(u,v)) printf("Y\n"); else printf("N\n"); } } return 0; }
前向星存图
/* 加边操作 */ void adde(int u,int v,int w) { a[++tot].pre=head[u]; a[tot].to=v; a[tot].w=w; head[u]=tot; } /* 遍历操作 */ for (int i=head[u];i;i=a[i].pre) { int v=a[i].to; }
KM求最优匹配、匈牙利算法求最大匹配
匈牙利算法求最大匹配
# include <iostream> # include <algorithm> # include <cstdio> # include <cstring> # include <cmath> using namespace std; const int MAXN=1005; int pre[MAXN],n,m,k,ans=0; bool vis[MAXN],mp[MAXN][MAXN]; bool find(int u) { for (int i=1;i<=m;i++) if ((!vis[i])&&(mp[u][i])) { vis[i]=true; if (pre[i]==-1||find(pre[i])){ pre[i]=u; return true; } } return false; } void solve() { memset(pre,-1,sizeof(pre)); for (int i=1;i<=n;i++){ memset(vis,false,sizeof(vis)); if (find(i)) ans++; } } int main() { scanf("%d%d%d",&n,&m,&k); memset(mp,false,sizeof(mp)); int u,v; for (int i=1;i<=k;i++) scanf("%d%d",&u,&v),mp[u][v]=true; solve(); printf("%d\n",ans); return 0; }
KM算法求最优匹配
# include <bits/stdc++.h> using namespace std; const int N=105,M=105; bool X[N],Y[N]; int mp[N][M],pre[N],lx[N],ly[M],n,m,k; bool find(int u) { X[u]=true; for (int v=1;v<=m;v++) if ((!Y[v])&&(lx[u]+ly[v]==mp[u][v])){ Y[v]=true; if (pre[v]==-1||find(pre[v])) { pre[v]=u; return true; } } return false; } int solve() { memset(pre,-1,sizeof(pre)); memset(lx,0,sizeof(lx)); memset(ly,0,sizeof(lx)); for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) lx[i]=max(lx[i],mp[i][j]); for (int w=1;w<=n;w++){ while (true) { memset(X,false,sizeof(X)); memset(Y,false,sizeof(Y)); int d=INT_MAX; if (find(w)) break; for (int i=1;i<=n;i++) if (X[i]) for (int j=1;j<=m;j++) if (!Y[j]) d=min(d,lx[i]+ly[j]-mp[i][j]); for (int i=1;i<=n;i++) if (X[i]) lx[i]-=d; for (int i=1;i<=m;i++) if (Y[i]) ly[i]+=d; } } int sum=0; for (int i=1;i<=n;i++) sum+=lx[i]; for (int i=1;i<=m;i++) sum+=ly[i]; return sum; } int main() { scanf("%d%d%d",&n,&m,&k); int u,v,w; memset(mp,-1,sizeof(mp)); while (k--) scanf("%d%d%d",&u,&v,&w),mp[u][v]=w; printf("%d\n",solve()); return 0; }
FF算法求最大流
// luogu-judger-enable-o2 # include <bits/stdc++.h> # define Rint register int using namespace std; const int MAXN=10005,MAXM=100005; struct rec{ int pre,to,w; }a[2*MAXM]; int head[MAXN],n,m,s,t,ans=0,tot=0; bool vis[MAXN]; inline int read() { int X=0,w=0; char c=0; while(c<'0'||c>'9') {w|=c=='-';c=getchar();} while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar(); return w?-X:X; } inline void adde(int u,int v,int w) { a[++tot].pre=head[u]; a[tot].to=v; a[tot].w=w; head[u]=tot; } inline int dfs(int u,int f) { if (u==t||f==0) return f; vis[u]=true; for (Rint i=head[u];i;i=a[i].pre){ int v=a[i].to,d; if (vis[v]) continue; if ((a[i].w>0)&&(d=dfs(v,min(f,a[i].w)))>0){ a[i].w-=d; if (i%2) a[i+1].w+=d; else a[i-1].w+=d; return d; } } return 0; } inline void FF() { while (true) { memset(vis,false,sizeof(vis)); int f=dfs(s,INT_MAX); if (f==0) break; ans+=f; } } int main() { n=read();m=read();s=read();t=read(); int u,v,w; for (Rint i=1;i<=m;i++){ u=read();v=read();w=read(); adde(u,v,w); adde(v,u,0); } ans=0; FF(); printf("%d\n",ans); return 0; }
qwq
*最小费用最大流
树上Hash
https://www.cnblogs.com/AseanA/p/7633174.html
如何进行树上hash,设f[i]为以i为节点的hash值,则
f[i]=sigma(f[j]*prime[j]) j为son[i]
其中prime为预处理出来的素数表···注意f[j]需要进行排序····
然后对于两颗待判定的树,将两颗树分别以树上每一个节点为根节点求hash值··将根节点的hash值储存起来排序然后两颗树一一比对··如果完全一样则两棵树就一样
数据结构模板:
树状数组模板(区间最大最小和)
单点修改区间求和:
# include <bits/stdc++.h> using namespace std; const int MAXN=500005; int c[MAXN],n,m; int lowbit(int x) { return x&(-x); } void update(int x,int y) { while (x<=n) { c[x]+=y; x+=lowbit(x); } } int query(int x) { int ret=0; while (x>0) { ret+=c[x]; x-=lowbit(x); } return ret; } int main() { scanf("%d%d",&n,&m); memset(c,0,sizeof(c)); for (int i=1;i<=n;i++) { int t; scanf("%d",&t); update(i,t); } for (int i=1;i<=m;i++) { int ch,x,y; scanf("%d%d%d",&ch,&x,&y); if (ch==1) update(x,y); else printf("%d\n",query(y)-query(x-1)); } return 0; }
区间修改,单点求值
# include <bits/stdc++.h> using namespace std; const int MAXN=500005; int c[MAXN],n,m; int lowbit(int x) { return x&(-x); } void update(int x,int y) { while (x<=n) { c[x]+=y; x+=lowbit(x); } } int query(int x) { int ret=0; while (x>0) { ret+=c[x]; x-=lowbit(x); } return ret; } int main() { scanf("%d%d",&n,&m); memset(c,0,sizeof(c)); int last=0; for (int i=1;i<=n;i++) { int t; scanf("%d",&t); update(i,t-last); last=t; } for (int i=1;i<=m;i++) { int ch,l,r,opx; scanf("%d",&ch); if (ch==1) { scanf("%d%d%d",&l,&r,&opx); update(l,opx); update(r+1,-opx); } else if (ch==2) { scanf("%d",&l); printf("%d\n",query(l)); } } return 0; }
区间修改区间求值
/* c1[i]表示维护原序列a[i]的差分数列 c2[i]表示维护(i-1)*c1[i] 显然a[i]=c1[1]+c1[2]+...+c1[i]; a[1]+a[2]+a[3]+..a[i]=(c1[1])+(c1[1]+c1[2])+...+(c1[1]+c1[2]+...+c1[i]) =i*(c1[1]+c1[2]+c1[3]+...+c1[i])-(0*c1[1]+1*c1[2]+2*c1[3]+...+(i-1)*c1[i]) 维护数组(i-1)*c1[i]的前缀和 a[1]+a[2]+a[3]+..a[i]=i*c1.query(i)-c2.query(i) a[1]+a[2]+a[3]+..a[r]=r*c1.query(r)-c2.query(r) a[1]+a[2]+a[3]+..a[l-1]=(l-1)*c1.query(l-1)-c2.query(l-1) a[l]+a[l+1]+...+a[r-1]+a[r]=(a[1]+a[2]+...+a[r])-(a[1]+a[2]+...+a[l-1]) = r*c1.query(r)-c2.query(r)-((l-1)*c1.query(l-1)-c2.query(l-1)) */ # include <bits/stdc++.h> using namespace std; typedef long long ll; const ll MAXN=500005; ll n,m; struct qwq{ ll c[MAXN]; ll lowbit(ll x) { return x&(-x); } void update(ll x,ll y) { while (x<=n) { c[x]+=y; x+=lowbit(x); } } ll query(ll x) { ll ret=0; while (x>0) { ret+=c[x]; x-=lowbit(x); } return ret; } }c1,c2; int main() { scanf("%lld%lld",&n,&m); ll last=0; for (ll i=1;i<=n;i++) { ll t; scanf("%lld",&t); c1.update(i,t-last); c2.update(i,(i-1)*(t-last)); last=t; } for (ll i=1;i<=m;i++) { ll ch,l,r,opx; scanf("%lld",&ch); if (ch==1) { scanf("%lld%lld%lld",&l,&r,&opx); c1.update(l,opx); c1.update(r+1,-opx); c2.update(l,(l-1)*opx); c2.update(r+1,-r*opx); } else if (ch==2) { scanf("%lld%lld",&l,&r); ll sum1=(l-1)*c1.query(l-1)-c2.query(l-1); ll sum2=r*c1.query(r)-c2.query(r); printf("%lld\n",sum2-sum1); } } return 0; }
线段树模板(区间最大最小和)
区间修改(加)区间求和(lazy标记)
# include <bits/stdc++.h> using namespace std; typedef long long ll; const int MAXN=100005; int n,m,opl,opr,opx; ll f[MAXN*3],a[MAXN],s[MAXN*3],ans; void build (int x,int l,int r) { if (l==r) { f[x]=a[l]; return; } int mid=(l+r)/2; build (2*x,l,mid); build (2*x+1,mid+1,r); f[x]=f[2*x]+f[2*x+1]; } void down(int x,int l,int r) { int mid=(l+r)/2; f[2*x]+=s[x]*(mid-l+1); f[2*x+1]+=s[x]*(r-mid); s[2*x]+=s[x]; s[2*x+1]+=s[x]; s[x]=0; } void update(int x,int l,int r) { if (opl<=l&&r<=opr) { f[x]+=(r-l+1)*opx; s[x]+=opx; return; } if (s[x]>0) down(x,l,r); int mid=(l+r)/2; if (opl<=mid) update(2*x,l,mid); if (opr>mid) update(2*x+1,mid+1,r); f[x]=f[2*x]+f[2*x+1]; } void query(int x,int l,int r) { if (opl<=l&&r<=opr) { ans+=f[x]; return; } int mid=(l+r)/2; if (s[x]>0) down(x,l,r); if (opl<=mid) query(2*x,l,mid); if (opr>mid) query(2*x+1,mid+1,r); } int main() { scanf("%d%d",&n,&m); for (int i=1;i<=n;i++) scanf("%d",&a[i]); build(1,1,n); int ch; for (int i=1;i<=m;i++) { scanf("%d",&ch); if (ch==1) scanf("%d%d%d",&opl,&opr,&opx),update(1,1,n); else if (ch==2) scanf("%d%d",&opl,&opr),ans=0,query(1,1,n),printf("%lld\n",ans); } return 0; }
LCT之树链剖分
/* 如题,已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作: 操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z 操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和 操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z 操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和 */ # include <bits/stdc++.h> # define MAXN 100005 using namespace std; typedef long long ll; int n,m,r,p,val[MAXN],b[MAXN]; struct Tree{ ll c[MAXN]; int lowbit(int x){ return x&(-x);} void update(int x,int y){ while (x<=n){ c[x]+=y; x+=lowbit(x); } } ll query(int x){ ll ret=0; while (x>0){ ret+=c[x]; x-=lowbit(x); } return ret; } }c1,c2; struct Edge{ int pre,to; }a[2*MAXN]; int head[MAXN],tot=0; void adde(int u,int v) { a[++tot].pre=head[u]; a[tot].to=v; head[u]=tot; } ll getsum(int l,int r) { return (ll) c1.query(r)*r-c2.query(r)-(l-1)*c1.query(l-1)+c2.query(l-1); } int f[MAXN],dep[MAXN],son[MAXN],size[MAXN]; void dfs1(int u,int fa,int depth)//f[],dep[],son[],size[] { f[u]=fa;dep[u]=depth;size[u]=1; for (int i=head[u];i;i=a[i].pre) { int v=a[i].to; if (v==fa) continue; dfs1(v,u,depth+1); size[u]+=size[v]; if (size[son[u]]<size[v]) son[u]=v; } } int w[MAXN],cntw=0,top[MAXN],old[MAXN]; void dfs2(int u,int tp) //w[],top[],old[] { w[u]=++cntw;top[u]=tp; old[cntw]=u; if (son[u]!=0) dfs2(son[u],tp); for (int i=head[u];i;i=a[i].pre) { int v=a[i].to; if (v==f[u]||v==son[u]) continue; dfs2(v,v); } } void change(int u,int v,int d) //此处u,v都为老编号 { int f1=top[u],f2=top[v]; while (f1!=f2){ if (dep[f1]<dep[f2]) swap(f1,f2),swap(u,v); c1.update(w[f1],d); c1.update(w[u]+1,-d); c2.update(w[f1],d*(w[f1]-1)); c2.update(w[u]+1,-d*w[u]); u=f[f1]; f1=top[u]; } if (dep[u]<dep[v]) swap(u,v); c1.update(w[v],d); c1.update(w[u]+1,-d); c2.update(w[v],d*(w[v]-1)); c2.update(w[u]+1,-d*w[u]); } ll lca(int u,int v) { int f1=top[u],f2=top[v]; ll ret=0ll; while (f1!=f2){ if (dep[f1]<dep[f2]) swap(f1,f2),swap(u,v); //w[f1]~w[u] ret=ret+getsum(w[f1],w[u]); u=f[f1]; f1=top[u]; } if (dep[u]<dep[v]) swap(u,v); //w[v]~w[u] ret=ret+getsum(w[v],w[u]); return ret%p; } int main() { scanf("%d%d%d%d",&n,&m,&r,&p); for (int i=1;i<=n;i++) scanf("%d",&val[i]); int u,v; for (int i=1;i<=n-1;i++) { scanf("%d%d",&u,&v); adde(u,v); adde(v,u); } dfs1(r,0,0); dfs2(r,0); for (int i=1;i<=n;i++) b[i]=val[old[i]]; for (int i=1;i<=n;i++) c1.update(i,b[i]-b[i-1]),c2.update(i,(b[i]-b[i-1])*(i-1)); int ch,x,y,z; for (int i=1;i<=m;i++) { scanf("%d%d",&ch,&x); if (ch==1) scanf("%d%d",&y,&z),change(x,y,z); else if (ch==2) scanf("%d",&y),printf("%lld\n",lca(x,y)%p); else if (ch==3) { scanf("%d",&z); int l=w[x],r=w[x]+size[x]-1; c1.update(l,z); c1.update(r+1,-z); c2.update(l,z*(l-1)); c2.update(r+1,-z*r); }else if (ch==4) { int l=w[x],r=w[x]+size[x]-1; ll ret=getsum(l,r); printf("%lld\n",ret%p); } } return 0; }
字典树(STL实现)
实数二分,整数二分答案
*线性基


 浙公网安备 33010602011771号
浙公网安备 33010602011771号