十大基础有用算法之深度优先搜索和广度优先搜索
深度优先搜索算法(Depth-First-Search),是搜索算法的一种。它沿着树的深度遍历树的节点。尽可能深的搜索树的分支。
当节点v的全部边都己被探寻过。搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的全部节点为止。假设还存在未被发现的节点,则选择当中一个作为源节点并重复以上过程。整个进程重复进行直到全部节点都被訪问为止。DFS属于盲目搜索。
深度优先搜索是图论中的经典算法,利用深度优先搜索算法能够产生目标图的对应拓扑排序表,利用拓扑排序表能够方便的解决非常多相关的图论问题。如最大路径问题等等。一般用堆数据结构来辅助实现DFS算法。
深度优先遍历图算法步骤:
1. 訪问顶点v;
2. 依次从v的未被訪问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被訪问;
3. 若此时图中尚有顶点未被訪问。则从一个未被訪问的顶点出发,又一次进行深度优先遍历,直到图中全部顶点均被訪问过为止。
上述描写叙述可能比較抽象。举个实例:
DFS 在訪问图中某一起始顶点 v 后,由 v 出发,訪问它的任一邻接顶点 w1;再从 w1 出发,訪问与 w1邻 接但还没有訪问过的顶点 w2。然后再从 w2 出发,进行类似的訪问,… 如此进行下去,直至到达全部的邻接顶点都被訪问过的顶点 u 为止。
接着。退回一步。退到前一次刚訪问过的顶点。看是否还有其他没有被訪问的邻接顶点。假设有,则訪问此顶点,之后再从此顶点出发,进行与前述类似的訪问;假设没有,就再退回一步进行搜索。反复上述过程,直到连通图中全部顶点都被訪问过为止。
深度优先搜索的图文介绍
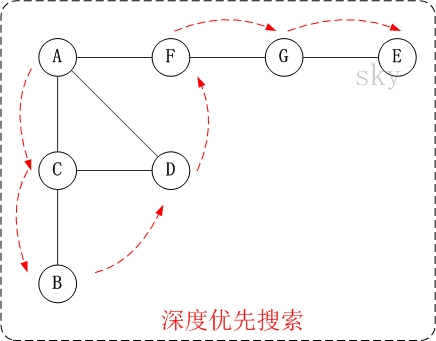
以下以"无向图"为例,来对深度优先搜索进行演示。
对上面的图G1进行深度优先遍历。从顶点A開始。
第1步:訪问A。
第2步:訪问(A的邻接点)C。
在第1步訪问A之后。接下来应该訪问的是A的邻接点。即"C,D,F"中的一个。
但在本文的实现中。顶点ABCDEFG是依照顺序存储,C在"D和F"的前面,因此,先訪问C。
第3步:訪问(C的邻接点)B。
在第2步訪问C之后。接下来应该訪问C的邻接点,即"B和D"中一个(A已经被訪问过。就不算在内)。
而因为B在D之前。先訪问B。
第4步:訪问(C的邻接点)D。
在第3步訪问了C的邻接点B之后,B没有未被訪问的邻接点;因此,返回到訪问C的还有一个邻接点D。
第5步:訪问(A的邻接点)F。
前面已经訪问了A,而且訪问完了"A的邻接点B的全部邻接点(包含递归的邻接点在内)"。因此。此时返回到訪问A的还有一个邻接点F。
第6步:訪问(F的邻接点)G。
第7步:訪问(G的邻接点)E。
因此訪问顺序是:A -> C -> B -> D -> F -> G -> E
以下以"有向图"为例,来对深度优先搜索进行演示。
对上面的图G2进行深度优先遍历。从顶点A開始。
第1步:訪问A。
第2步:訪问B。
在訪问了A之后。接下来应该訪问的是A的出边的还有一个顶点。即顶点B。
第3步:訪问C。
在訪问了B之后,接下来应该訪问的是B的出边的还有一个顶点。即顶点C,E,F。在本文实现的图中,顶点ABCDEFG依照顺序存储。因此先訪问C。
第4步:訪问E。
接下来訪问C的出边的还有一个顶点。即顶点E。
第5步:訪问D。
接下来訪问E的出边的还有一个顶点,即顶点B,D。
顶点B已经被訪问过,因此訪问顶点D。
第6步:訪问F。
接下应该回溯"訪问A的出边的还有一个顶点F"。
第7步:訪问G。
因此訪问顺序是:A -> B -> C -> E -> D -> F -> G
以下介绍广度优先搜索
广度优先搜索算法(Breadth-First-Search)。是一种图形搜索算法。
简单的说,BFS是从根节点開始,沿着树(图)的宽度遍历树(图)的节点。
假设全部节点均被訪问。则算法中止。BFS相同属于盲目搜索。一般用队列数据结构来辅助实现BFS算法。
算法步骤:
1. 首先将根节点放入队列中。
2. 从队列中取出第一个节点。并检验它是否为目标。
- 假设找到目标。则结束搜寻并回传结果。
- 否则将它全部尚未检验过的直接子节点增加队列中。
3. 若队列为空,表示整张图都检查过了——亦即图中没有欲搜寻的目标。
结束搜寻并回传“找不到目标”。
4. 反复步骤2。
广度优先搜索图文介绍
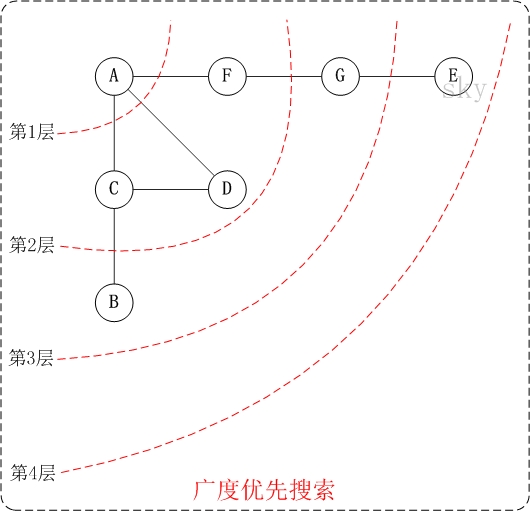
以下以"无向图"为例。来对广度优先搜索进行演示。还是以上面的图G1为例进行说明。
第1步:訪问A。
第2步:依次訪问C,D,F。
在訪问了A之后。接下来訪问A的邻接点。
前面已经说过,在本文实现中,顶点ABCDEFG依照顺序存储的,C在"D和F"的前面,因此。先訪问C。
再訪问完C之后。再依次訪问D,F。
第3步:依次訪问B,G。
在第2步訪问完C,D,F之后,再依次訪问它们的邻接点。首先訪问C的邻接点B,再訪问F的邻接点G。
第4步:訪问E。
在第3步訪问完B,G之后。再依次訪问它们的邻接点。仅仅有G有邻接点E,因此訪问G的邻接点E。
因此訪问顺序是:A -> C -> D -> F -> B -> G -> E
以下以"有向图"为例,来对广度优先搜索进行演示。还是以上面的图G2为例进行说明。
第1步:訪问A。
第2步:訪问B。
第3步:依次訪问C,E,F。
在訪问了B之后,接下来訪问B的出边的还有一个顶点。即C,E,F。前面已经说过,在本文实现中,顶点ABCDEFG依照顺序存储的,因此会先訪问C,再依次訪问E,F。
第4步:依次訪问D,G。
在訪问完C,E,F之后,再依次訪问它们的出边的还有一个顶点。还是依照C,E,F的顺序訪问,C的已经所有訪问过了,那么就仅仅剩下E,F;先訪问E的邻接点D,再訪问F的邻接点G。
因此訪问顺序是:A -> B -> C -> E -> F -> D -> G
借用知乎里的一句话,Talk is cheap,show me your code.邻接矩阵的无向图:(代码经过实验,可产生如上的訪问顺序)
#include <iostream>
using namespace std;
const int MAX = 100;
class MatrixUDG
{
public:
MatrixUDG();//创建图。自己输入数据
MatrixUDG(char vexs[],int vlen,char edges[][2],int elen);//使用已经存在的矩阵
~MatrixUDG();
void DFS();
void BFS();
void print();
private:
char mVexs[MAX];//顶点集合
int mVexNum; //顶点数
int mEdgNum; //边数
int mMatrix[MAX][MAX]; //邻接矩阵
char readChar();//读取一个输入字符串
int getPosition(char ch);//返回ch在mMatrix矩阵中的位置
int firstVertex(int v);//返回顶点v的第一个邻接顶点的索引。失败则返回-1
int nextVertex(int v,int w);//返回顶点v的相对于顶点w的下一个索引,失败则返回-1
void DFS(int i,int *visted);//深度优先搜索遍历图的递归实现
};
MatrixUDG::MatrixUDG()
{
char c1,c2;
int i,p1,p2;
//input vertex and edge number
cout<<"input vertex number:";
cin>>mVexNum;
cout<<"input edge number:";
cin>>mEdgNum;
if(mVexNum<1 || mEdgNum<1 || mEdgNum>mVexNum*(mVexNum - 1))
{
cout<<"input error:invalid parameters!";
return;
}
// init vertex
for(i = 0;i<mVexNum;i++)
{
cout<<"vertex("<<i<<")"<<endl;
mVexs[i] = readChar();
}
//init edge
for(i = 0;i<mEdgNum;i++)
{
cout<<"edge("<<i<<")";
c1 = readChar();
c2 = readChar();
p1 = getPosition(c1);
p2 = getPosition(c2);
if(p1 == -1 || p2 == -1)
{
cout<<"input error:invalid parameters."<<endl;
return;
}
mMatrix[p1][p2] = 1;
mMatrix[p2][p1] = 1;
}
}
MatrixUDG::MatrixUDG(char vexs[], int vlen, char edges[][2], int elen)
{
int i, p1, p2;
// 初始化"顶点数"和"边数"
mVexNum = vlen;
mEdgNum = elen;
// 初始化"顶点"
for (i = 0; i < mVexNum; i++)
mVexs[i] = vexs[i];
// 初始化"边"
for (i = 0; i < mEdgNum; i++)
{
// 读取边的起始顶点和结束顶点
p1 = getPosition(edges[i][0]);
p2 = getPosition(edges[i][1]);
mMatrix[p1][p2] = 1;
mMatrix[p2][p1] = 1;
}
}
MatrixUDG::~MatrixUDG()
{}
int MatrixUDG::getPosition(char ch)
{
int i;
for(i = 0;i<mVexNum;i++)
if(mVexs[i] == ch)
return i;
return -1;
}
char MatrixUDG::readChar()
{
char ch;
do
{
cin>>ch;
}while(!((ch>='a' && ch<='z') || (ch>='A' && ch<='Z')));
return ch;
}
int MatrixUDG::firstVertex(int v)
{
int i;
if(v<0 || v>(mVexNum - 1))
return -1;
for(i = 0;i<mVexNum;i++)
{
if(mMatrix[v][i] == 1)
return i;
}
return -1;
}
int MatrixUDG::nextVertex(int v,int w)
{
int i;
if(v<0 || v>(mVexNum - 1) || w<0 || w>(mVexNum - 1))
return -1;
for(i = w+1;i<mVexNum;i++)
{
if(mMatrix[v][i] == 1)
return i;
}
return -1;
}
void MatrixUDG::DFS(int i,int *visted)
{
int w;
visted[i] = 1;
cout<<mVexs[i]<<' ';
for(w = firstVertex(i);w>=0;w = nextVertex(i,w))
{
if(!visted[w])
DFS(w,visted);
}
}
void MatrixUDG::DFS()
{
int i;
int visted[MAX];
for(i = 0;i<mVexNum;i++)
visted[i] = 0;
cout<<"DFS:";
for(i = 0;i<mVexNum;i++)
{
if(!visted[i])
DFS(i,visted);
}
cout<<endl;
}
void MatrixUDG::BFS()
{
int head = 0;
int rear = 0;
int queue[MAX];
int visted[MAX];
int i,j,k;
for(i = 0;i<mVexNum;i++)
visted[i] = 0;
cout<<"BFS:";
for(i = 0;i<mVexNum;i++)
{
if(!visted[i])
{
visted[i] = 1;
cout<<mVexs[i]<<' ';
queue[rear++] = i;//in queue
}
while(head != rear)
{
j = queue[head++];
for(k = firstVertex(j);k >= 0;k = nextVertex(j,k))
{
if(!visted[k])
{
visted[k] = 1;
cout<<mVexs[k]<<" ";
queue[rear++] = k;
}
}
}
}
cout<<endl;
}
void MatrixUDG::print()
{
int i,j;
cout<<"Matrix Graph:"<<endl;
cout<<" A B C D E F G"<<endl;
for(i = 0;i<mVexNum;i++)
{
cout<<mVexs[i]<<" ";
for(j = 0;j<mVexNum;j++)
cout<<(mMatrix[i][j] == 1?1:0)<<" ";
cout<<endl;
}
}
int main()
{
char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
char edges[][2] = {
{'A', 'C'},
{'A', 'D'},
{'A', 'F'},
{'B', 'C'},
{'C', 'D'},
{'E', 'G'},
{'F', 'G'}};
int vlen = sizeof(vexs)/sizeof(vexs[0]);
int elen = sizeof(edges)/sizeof(edges[0]);
MatrixUDG* pG;
// 自己定义"图"(输入矩阵队列)
//pG = new MatrixUDG();
// 採用已有的"图"
pG = new MatrixUDG(vexs, vlen, edges, elen);
pG->print(); // 打印图
pG->DFS(); // 深度优先遍历
pG->BFS(); // 广度优先遍历
return 0;
}
没有经过检验。
当中有向图的修改较小。仅仅须要在加入边的时候加入一条边就可以。不再显示代码。
下面是邻接表的实现,关键的是节点定义和訪问方法的改变。
#include <iomanip>
#include <iostream>
#include <vector>
using namespace std;
#define MAX 100
// 邻接表
class ListUDG
{
private: // 内部类
// 邻接表中表相应的链表的顶点
class ENode
{
public:
int ivex; // 该边所指向的顶点的位置
ENode *nextEdge; // 指向下一条弧的指针
};
// 邻接表中表的顶点
class VNode
{
public:
char data; // 顶点信息
ENode *firstEdge; // 指向第一条依附该顶点的弧
};
private: // 私有成员
int mVexNum; // 图的顶点的数目
int mEdgNum; // 图的边的数目
VNode mVexs[MAX];
public:
// 创建邻接表相应的图(自己输入)
ListUDG();
// 创建邻接表相应的图(用已提供的数据)
ListUDG(char vexs[], int vlen, char edges[][2], int elen);
~ListUDG();
// 深度优先搜索遍历图
void DFS();
// 广度优先搜索(相似于树的层次遍历)
void BFS();
// 打印邻接表图
void print();
private:
// 读取一个输入字符
char readChar();
// 返回ch的位置
int getPosition(char ch);
// 深度优先搜索遍历图的递归实现
void DFS(int i, int *visited);
// 将node节点链接到list的最后
void linkLast(ENode *list, ENode *node);
};
/*
* 创建邻接表相应的图(自己输入)
*/
ListUDG::ListUDG()
{
char c1, c2;
int v, e;
int i, p1, p2;
ENode *node1, *node2;
// 输入"顶点数"和"边数"
cout << "input vertex number: ";
cin >> mVexNum;
cout << "input edge number: ";
cin >> mEdgNum;
if ( mVexNum < 1 || mEdgNum < 1 || (mEdgNum > (mVexNum * (mVexNum-1))))
{
cout << "input error: invalid parameters!" << endl;
return ;
}
// 初始化"邻接表"的顶点
for(i=0; i<mVexNum; i++)
{
cout << "vertex(" << i << "): ";
mVexs[i].data = readChar();
mVexs[i].firstEdge = NULL;
}
// 初始化"邻接表"的边
for(i=0; i<mEdgNum; i++)
{
// 读取边的起始顶点和结束顶点
cout << "edge(" << i << "): ";
c1 = readChar();
c2 = readChar();
p1 = getPosition(c1);
p2 = getPosition(c2);
// 初始化node1
node1 = new ENode();
node1->ivex = p2;
// 将node1链接到"p1所在链表的末尾"
if(mVexs[p1].firstEdge == NULL)
mVexs[p1].firstEdge = node1;
else
linkLast(mVexs[p1].firstEdge, node1);
// 初始化node2
node2 = new ENode();
node2->ivex = p1;
// 将node2链接到"p2所在链表的末尾"
if(mVexs[p2].firstEdge == NULL)
mVexs[p2].firstEdge = node2;
else
linkLast(mVexs[p2].firstEdge, node2);
}
}
/*
* 创建邻接表相应的图(用已提供的数据)
*/
ListUDG::ListUDG(char vexs[], int vlen, char edges[][2], int elen)
{
char c1, c2;
int i, p1, p2;
ENode *node1, *node2;
// 初始化"顶点数"和"边数"
mVexNum = vlen;
mEdgNum = elen;
// 初始化"邻接表"的顶点
for(i=0; i<mVexNum; i++)
{
mVexs[i].data = vexs[i];
mVexs[i].firstEdge = NULL;
}
// 初始化"邻接表"的边
for(i=0; i<mEdgNum; i++)
{
// 读取边的起始顶点和结束顶点
c1 = edges[i][0];
c2 = edges[i][1];
p1 = getPosition(c1);
p2 = getPosition(c2);
// 初始化node1
node1 = new ENode();
node1->ivex = p2;
// 将node1链接到"p1所在链表的末尾"
if(mVexs[p1].firstEdge == NULL)
mVexs[p1].firstEdge = node1;
else
linkLast(mVexs[p1].firstEdge, node1);
// 初始化node2
node2 = new ENode();
node2->ivex = p1;
// 将node2链接到"p2所在链表的末尾"
if(mVexs[p2].firstEdge == NULL)
mVexs[p2].firstEdge = node2;
else
linkLast(mVexs[p2].firstEdge, node2);
}
}
/*
* 析构函数
*/
ListUDG::~ListUDG()
{
}
/*
* 将node节点链接到list的最后
*/
void ListUDG::linkLast(ENode *list, ENode *node)
{
ENode *p = list;
while(p->nextEdge)
p = p->nextEdge;
p->nextEdge = node;
}
/*
* 返回ch的位置
*/
int ListUDG::getPosition(char ch)
{
int i;
for(i=0; i<mVexNum; i++)
if(mVexs[i].data==ch)
return i;
return -1;
}
/*
* 读取一个输入字符
*/
char ListUDG::readChar()
{
char ch;
do {
cin >> ch;
} while(!((ch>='a'&&ch<='z') || (ch>='A'&&ch<='Z')));
return ch;
}
/*
* 深度优先搜索遍历图的递归实现
*/
void ListUDG::DFS(int i, int *visited)
{
ENode *node;
visited[i] = 1;
cout << mVexs[i].data << " ";
node = mVexs[i].firstEdge;
while (node != NULL)
{
if (!visited[node->ivex])
DFS(node->ivex, visited);
node = node->nextEdge;
}
}
/*
* 深度优先搜索遍历图
*/
void ListUDG::DFS()
{
int i;
int visited[MAX]; // 顶点訪问标记
// 初始化全部顶点都没有被訪问
for (i = 0; i < mVexNum; i++)
visited[i] = 0;
cout << "DFS: ";
for (i = 0; i < mVexNum; i++)
{
if (!visited[i])
DFS(i, visited);
}
cout << endl;
}
/*
* 广度优先搜索(相似于树的层次遍历)
*/
void ListUDG::BFS()
{
int head = 0;
int rear = 0;
int queue[MAX]; // 辅组队列
int visited[MAX]; // 顶点訪问标记
int i, j, k;
ENode *node;
for (i = 0; i < mVexNum; i++)
visited[i] = 0;
cout << "BFS: ";
for (i = 0; i < mVexNum; i++)
{
if (!visited[i])
{
visited[i] = 1;
cout << mVexs[i].data << " ";
queue[rear++] = i; // 入队列
}
while (head != rear)
{
j = queue[head++]; // 出队列
node = mVexs[j].firstEdge;
while (node != NULL)
{
k = node->ivex;
if (!visited[k])
{
visited[k] = 1;
cout << mVexs[k].data << " ";
queue[rear++] = k;
}
node = node->nextEdge;
}
}
}
cout << endl;
}
/*
* 打印邻接表图
*/
void ListUDG::print()
{
int i,j;
ENode *node;
cout << "List Graph:" << endl;
for (i = 0; i < mVexNum; i++)
{
cout << i << "(" << mVexs[i].data << "): ";
node = mVexs[i].firstEdge;
while (node != NULL)
{
cout << node->ivex << "(" << mVexs[node->ivex].data << ") ";
node = node->nextEdge;
}
cout << endl;
}
}
int main()
{
char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
char edges[][2] = {
{'A', 'C'},
{'A', 'D'},
{'A', 'F'},
{'B', 'C'},
{'C', 'D'},
{'E', 'G'},
{'F', 'G'}};
int vlen = sizeof(vexs)/sizeof(vexs[0]);
int elen = sizeof(edges)/sizeof(edges[0]);
ListUDG* pG;
// 自己定义"图"(输入矩阵队列)
//pG = new ListUDG();
// 採用已有的"图"
pG = new ListUDG(vexs, vlen, edges, elen);
pG->print(); // 打印图
pG->DFS(); // 深度优先遍历
pG->BFS(); // 广度优先遍历
return 0;
}







 浙公网安备 33010602011771号
浙公网安备 33010602011771号