完整教程:图解向量的加减
图解向量的加减
二维空间(R2\mathbb{R}^2R2)里的向量
R\mathbb{R}R 代表 全体实数的集合(Set of Real Numbers),Real 是“实数的”形容词形式,取首字母 R 作为缩写。
Rn\mathbb{R}^nRn 就是 nnn维实数空间实数包括所有有理数(整数、分数)和无理数(如π\piπ、2\sqrt{2}2)。
平面中的向量v\mathbf{v}v表示为列向量v=(a1a2)\mathbf{v} = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}v=(a1a2),其中a1a_1a1是向量在xxx轴方向的分量,a2a_2a2是yyy轴方向的分量。
向量的长度(也叫“模长”)用符号∥v∥\|\mathbf{v}\|∥v∥表示,计算方法基于勾股定理,公式为:
∥v∥=a12+a22
\|\mathbf{v}\| = \sqrt{a_1^2 + a_2^2}∥v∥=a12+a22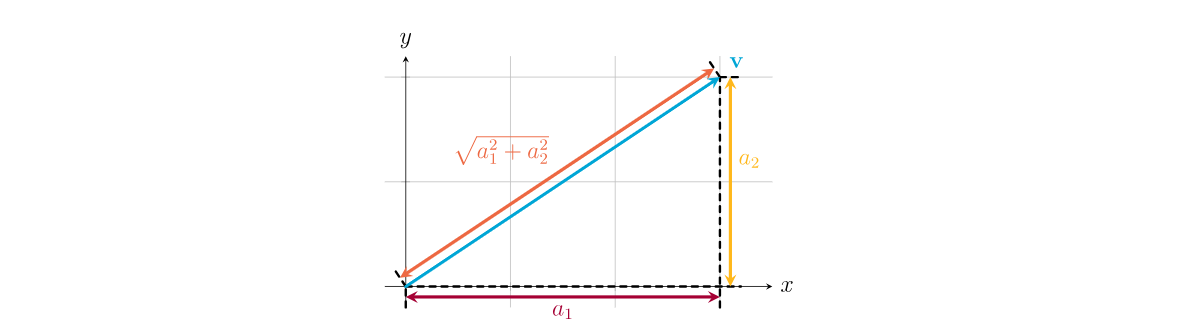
向量v\mathbf{v}v从原点出发,a1a_1a1(红色水平段)、a2a_2a2(黄色垂直段)与v\mathbf{v}v本身构成直角三角形——直角边是a1a_1a1和a2a_2a2,斜边就是向量v\mathbf{v}v
三维空间(R3\mathbb{R}^3R3)里的向量
向量v\mathbf{v}v表示为列向量:
v=(a1a2a3)
\mathbf{v} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}v=a1a2a3
其中a1a_1a1、a2a_2a2、a3a_3a3向量在就是分别xxx轴、yyy轴、zzz轴方向的分量。
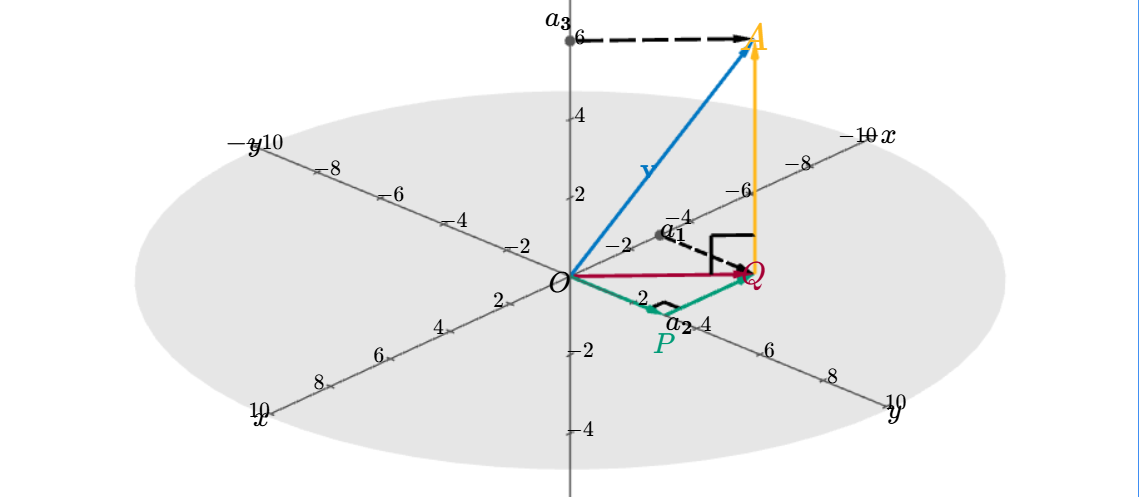
图里涵盖两个直角三角形
x-y平面内:在图的灰色平面(x-y平面)中,分量a1a_1a1、a2a_2a2构成直角三角形ΔOPQ\Delta OPQΔOPQ(直角在PPP),因此x-y平面内的向量长度满足:
OQ2=OP2+PQ2=a12+a22
OQ^2 = OP^2 + PQ^2 = a_1^2 + a_2^2OQ2=OP2+PQ2=a12+a22
空间中:x-y平面的向量长度OQOQOQ,与z轴分量a3a_3a3(对应线段QAQAQA)构成直角三角形ΔOQA\Delta OQAΔOQA(直角在QQQ),再次用勾股定理:
OA2=OQ2+QA2=a12+a22+a32
OA^2 = OQ^2 + QA^2 = a_1^2 + a_2^2 + a_3^2OA2=OQ2+QA2=a12+a22+a32
向量v\mathbf{v}v的长度(模长)∥v∥\|\mathbf{v}\|∥v∥就是线段OAOAOA的长度
∥v∥=a12+a22+a32
\|\mathbf{v}\| = \sqrt{a_1^2 + a_2^2 + a_3^2}∥v∥=a12+a22+a32
向量加法
把向量(箭头)看作简单的路线:
箭头方向= 行进方向;
箭头长度= 行进距离。
若要走同方向、两倍距离,就是把箭头(向量v1\mathbf{v}_1v1)拉伸2倍,对应向量数乘2v12\mathbf{v}_12v1。
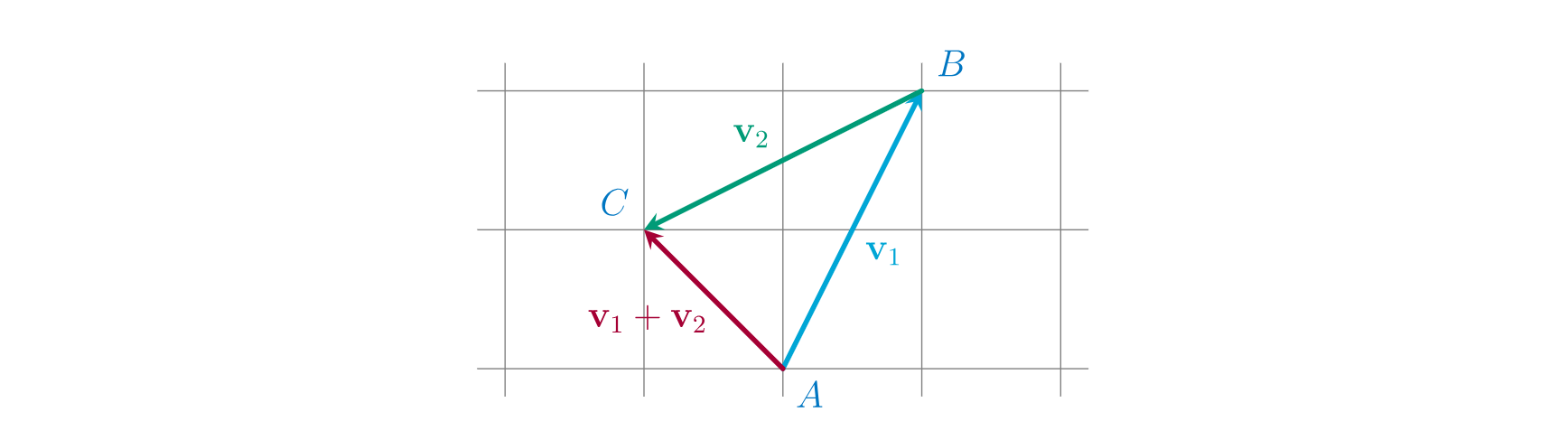
用三角形法则:
先沿向量v1\mathbf{v}_1v1从点AAA走到BBB;
再沿向量v2\mathbf{v}_2v2从点BBB走到CCC;
总路线(从AAA到CCC)对应的箭头,就是v1+v2\mathbf{v}_1 + \mathbf{v}_2v1+v2(图中红色箭头)。
代数表示(列向量)
向量用v=(xy)\mathbf{v} = \begin{pmatrix} x \\ y \end{pmatrix}v=(xy)表示:
xxx:水平方向(右为正、左为负);
yyy:垂直方向(上为正、下为负)。
比如例子里:v1=(12)\mathbf{v}_1 = \begin{pmatrix} 1 \\ 2 \end{pmatrix}v1=(12),v2=(−2−1)\mathbf{v}_2 = \begin{pmatrix} -2 \\ -1 \end{pmatrix}v2=(−2−1)。
分量对应相加
几何上的路线组合,对应代数里的分量相加:
v1+v2=(1+(−2)2+(−1))=(−11)
\mathbf{v}_1 + \mathbf{v}_2 = \begin{pmatrix} 1 + (-2) \\ 2 + (-1) \end{pmatrix} = \begin{pmatrix} -1 \\ 1 \end{pmatrix}v1+v2=(1+(−2)2+(−1))=(−11)
(v3=(−11)\mathbf{v}_3 = \begin{pmatrix} -1 \\ 1 \end{pmatrix}v3=(−11))和几何上从AAA到CCC的路线完全一致。
平行四边形法则(Parallelogram Law)
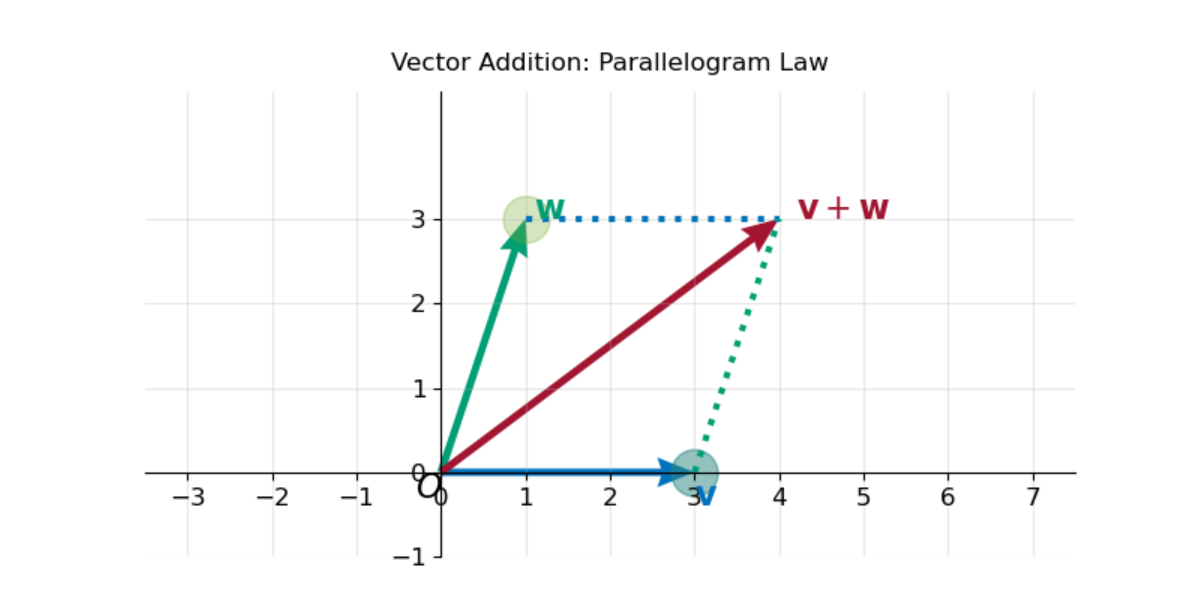
向量 v\mathbf{v}v (蓝色):在 x 轴上延伸 3 个单位。
v=[30]\mathbf{v} = \begin{bmatrix} 3 \\ 0 \end{bmatrix}v=[30]
向量 w\mathbf{w}w (绿色):x 轴方向 1 个单位,y 轴方向 3 个单位。
w=[13]\mathbf{w} = \begin{bmatrix} 1 \\ 3 \end{bmatrix}w=[13]
向量加法将对应分量相加:就是就
v+w=[3+10+3]=[43]\mathbf{v} + \mathbf{w} = \begin{bmatrix} 3 + 1 \\ 0 + 3 \end{bmatrix} = \begin{bmatrix} 4 \\ 3 \end{bmatrix}v+w=[3+10+3]=[43]
图中红色向量(合向量)指向的坐标就是这正(4,3)(4, 3)(4,3)
把底部的向量就是图中也隐含了三角形法则。看那条蓝色的虚线(在上方),它其实就v\mathbf{v}v 平移到了 w\mathbf{w}w的头部。这意味着:先走w\mathbf{w}w的路程,接着走v\mathbf{v}v的路程,最终到达的终点是一样的。
绘图源码在文末
垂直
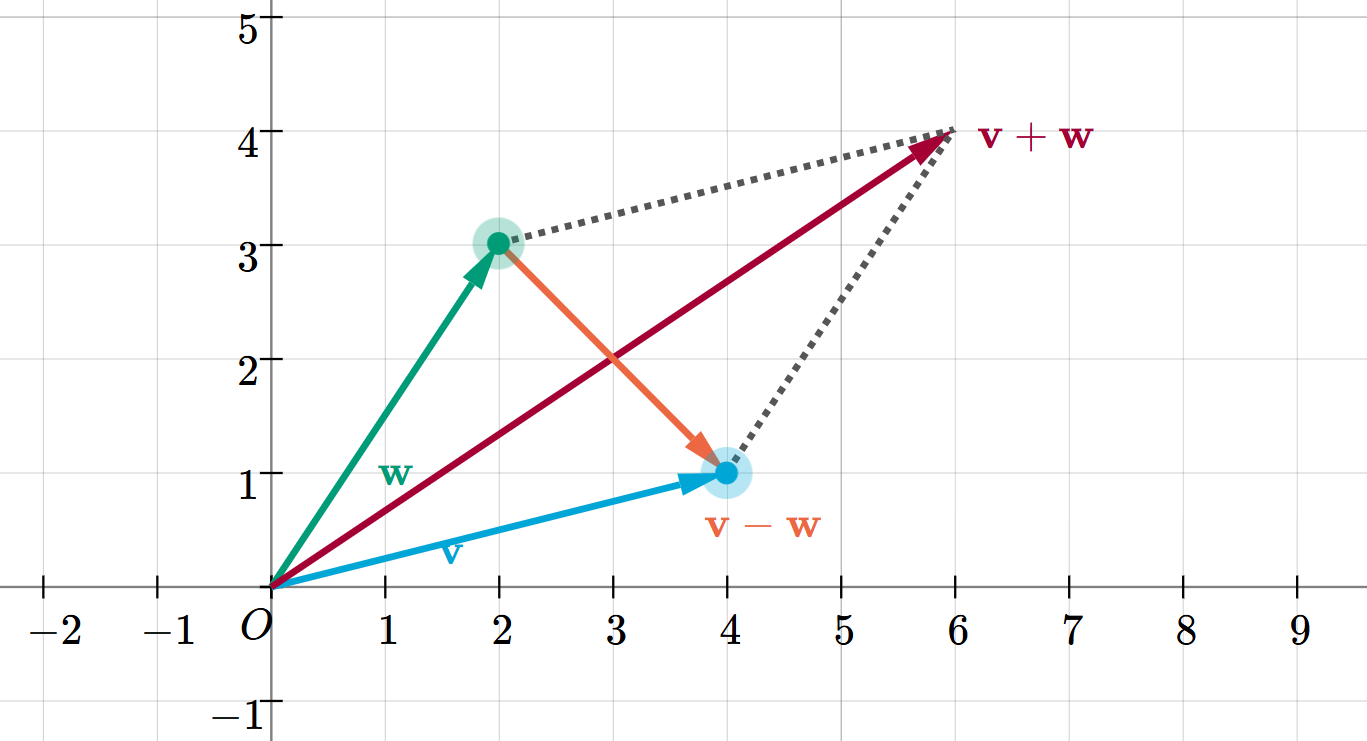
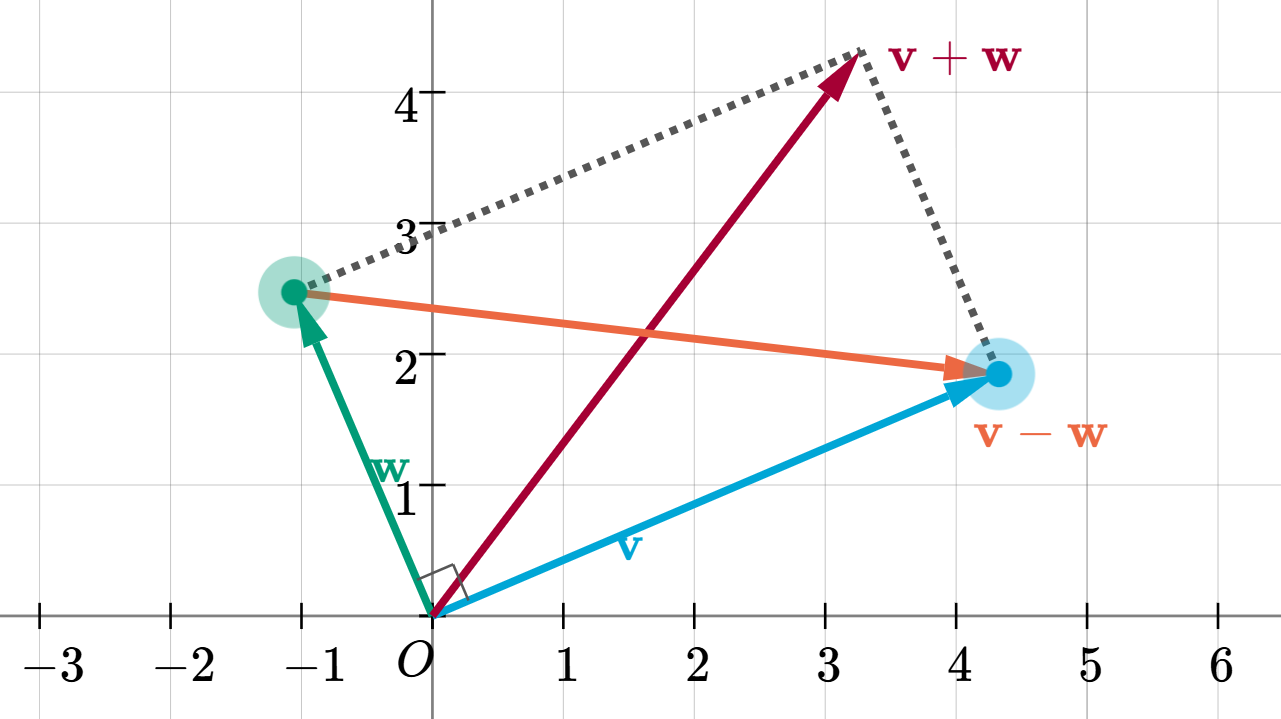
两个向量v\mathbf{v}v、w\mathbf{w}w可以张成一个平行四边形:
当且仅当v\mathbf{v}v和w\mathbf{w}w垂直时,这个平行四边形是矩形(矩形的邻边垂直)。
矩形的特征是“对角线长度相等”,对应到向量上:
矩形的两条对角线恰好是向量的和(v+w\mathbf{v}+\mathbf{w}v+w)与差(v−w\mathbf{v}-\mathbf{w}v−w),向量垂直等价于这两个对角线的模长相等,即:
∥v+w∥=∥v−w∥
\|\mathbf{v} + \mathbf{w}\| = \|\mathbf{v} - \mathbf{w}\|∥v+w∥=∥v−w∥
绘图源码
import matplotlib.pyplot as plt
import numpy as np
def draw_vector_addition():
# 1. 设置画布
fig, ax = plt.subplots(figsize=(8, 4.5))
# 定义向量坐标
# v: 起点(0,0), 终点(3,0)
# w: 起点(0,0), 终点(1,3)
v = np.array([3, 0])
w = np.array([1, 3])
resultant = v + w # 结果向量 (4, 3)
# 2. 绘制向量 (Quiver)
# 参数: x起点, y起点, x分量, y分量
# 蓝色向量 v
vector_line_width=0.008
ax.quiver(0, 0, v[0], v[1], angles='xy', scale_units='xy', scale=1,
color='#0072BD', width=vector_line_width, headwidth=4, headlength=5)
# 绿色向量 w
ax.quiver(0, 0, w[0], w[1], angles='xy', scale_units='xy', scale=1,
color='#009E73', width=vector_line_width, headwidth=4, headlength=5)
# 红色合向量 v + w
ax.quiver(0, 0, resultant[0], resultant[1], angles='xy', scale_units='xy', scale=1,
color='#A2142F', width=vector_line_width, headwidth=4, headlength=5)
# 3. 绘制平行四边形的虚线辅助线
# 上方的虚线 (平行于 v,从 w 的头部开始)
ax.plot([w[0], resultant[0]], [w[1], resultant[1]],
color='#0072BD', linestyle=':', linewidth=3)
# 右侧的虚线 (平行于 w,从 v 的头部开始)
ax.plot([v[0], resultant[0]], [v[1], resultant[1]],
color='#009E73', linestyle=':', linewidth=3)
# 4. 添加装饰性圆圈 (高光效果)
point_size = 500
ax.scatter([v[0], w[0]], [v[1], w[1]], s=point_size, color='#77AC30', alpha=0.3, zorder=1) # 绿色晕影
ax.scatter([v[0]], [v[1]], s=point_size, color='#0072BD', alpha=0.3, zorder=1) # 蓝色晕影
# 5. 添加文字标签
ax.text(v[0], v[1]-0.4, r'$\mathbf{v}$', color='#0072BD', fontsize=16, fontweight='bold')
ax.text(w[0]+0.1, w[1], r'$\mathbf{w}$', color='#009E73', fontsize=16, fontweight='bold')
ax.text(resultant[0]+0.2, resultant[1], r'$\mathbf{v} + \mathbf{w}$', color='#A2142F', fontsize=16, fontweight='bold')
ax.text(-0.3, -0.3, '$O$', fontsize=16, style='italic')
# 6. 配置坐标轴和网格
ax.set_xlim(-3.5, 7.5)
ax.set_ylim(-1, 4.5)
ax.set_aspect('equal') # 保证比例一致,看起来是正方形网格
ax.grid(True, linestyle='-', alpha=0.3)
# 移动坐标轴脊柱到中心 (0,0)
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
# 设置刻度
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
plt.xticks(np.arange(-3, 8, 1), fontsize=12)
plt.yticks(np.arange(-1, 4, 1), fontsize=12)
plt.title("Vector Addition: Parallelogram Law", y=1.02)
plt.show()
draw_vector_addition()


 浙公网安备 33010602011771号
浙公网安备 33010602011771号