【C++】并查集的原理与使用 - 教程

各位读者大佬好，我是落羽！一个坚持不断学习进步的学生。
如果您觉得我的文章还不错，欢迎多多互三分享交流，一起学习进步！
也欢迎关注我的blog主页:落羽的落羽

文章目录

• 一、并查集的概念
• 二、并查集的实现
• 三、算法题中的应用

一、并查集的概念

在一些场景中，需要将n个不同元素划分为一些不相交的集合。开始时，每个元素各成一个元素，然后按一定的规律将属于同一组的元素合并。这个过程中需要反复用到查询一个元素是否属于某个集合的算法。适合用于这种场景的数据结构是并查集（Union-Find Set）！

并查集的底层结构本质上是一片森林（多棵树的集合）

比如，我现在有九个数据元素，给他们编号0~8：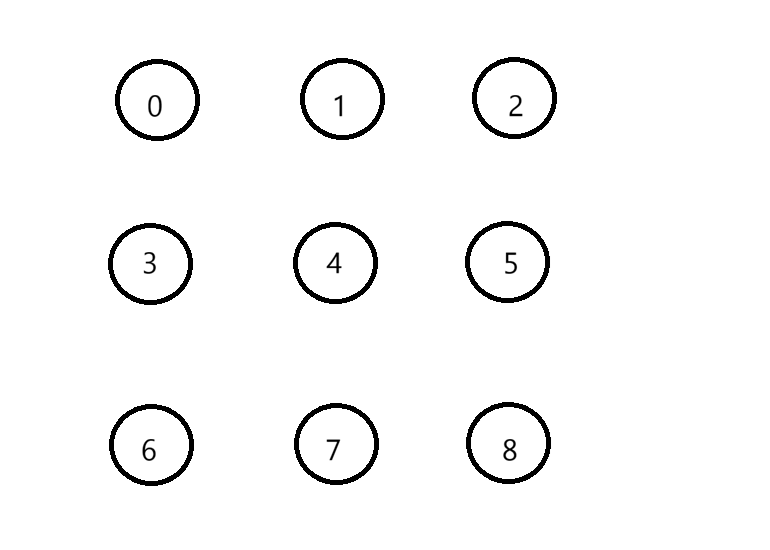

按照某种需求，这些数据被分组合并为：

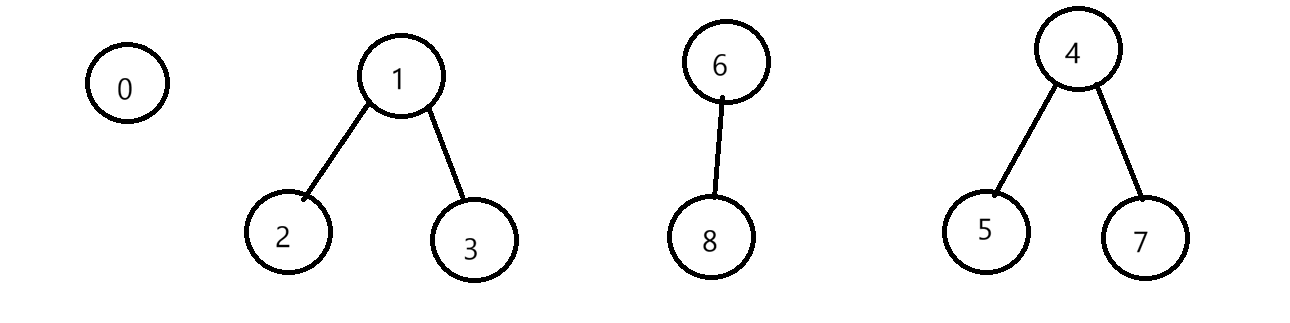
按照其他需求，这些树可以继续合并下去…

而这个森林，可以用一个数组记录下来元素的关系！
我们可以规定并查集用数组下标代表每个元素，数组内容代表元素之间的关系：

• 数组下标代表元素编号
• 如果数组内容为负整数，代表这个下标是根，绝对值表示它这棵树的元素个数
• 如果数组内容为非负整数，代表这个下标不是根，数组内容是它的父亲在数组中的下标

比如，上面的森林例子，用并查集数组表示，就是：

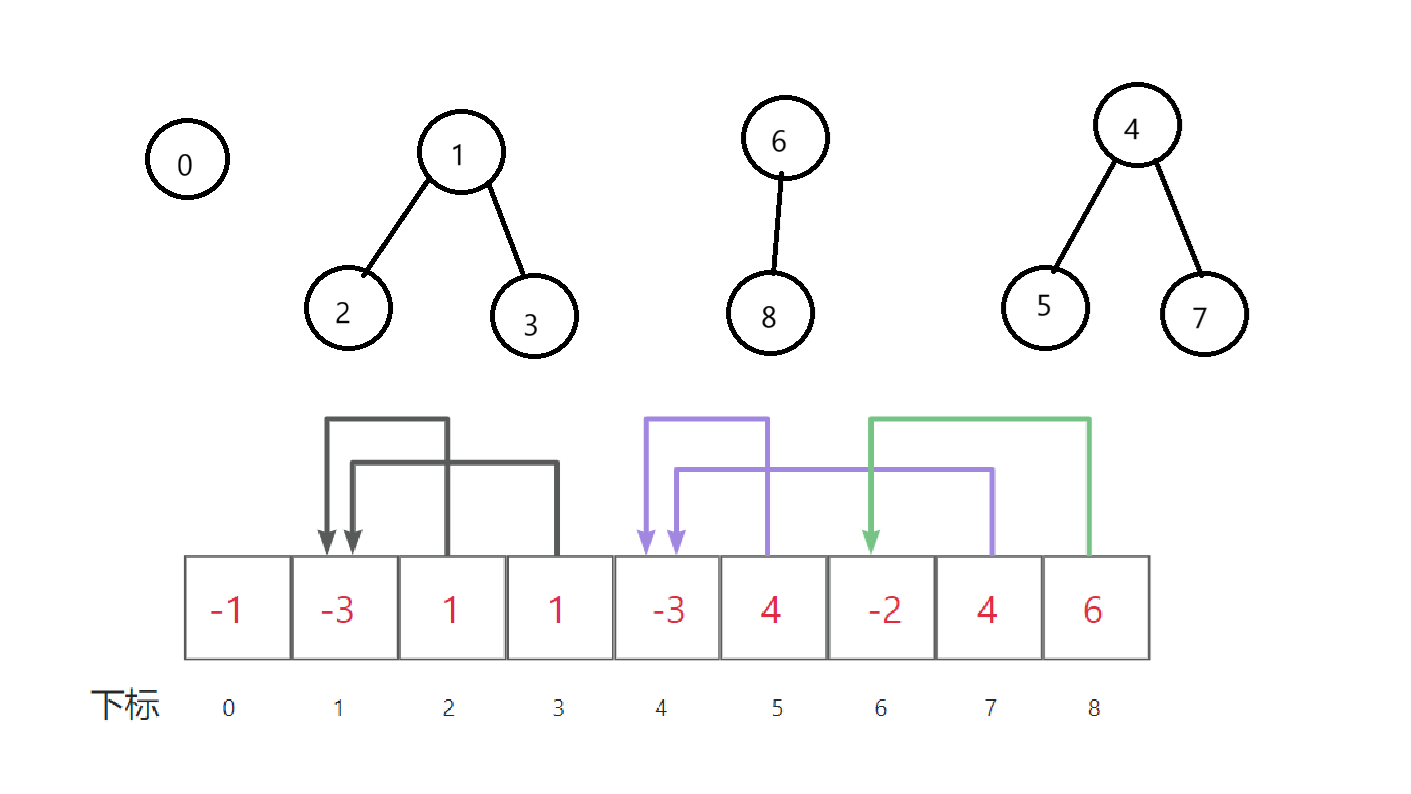
如果元素的数据类型不能直接作为数组下标，只要在实现中用std::map之类的结构，建立元素到下标的映射关系，就能解决了！

通过并查集的特点，可以看出并查集一般能解决：

• 查找元素属于哪个集合：沿着数组一直找到元素为负数，就是根
• 查看两个元素是否属于一个集合：看看这两个元素的根是否相同
• 将两个集合归并为一个集合：假如要将下标a的树合并到下标b的树中，arr[b] += arr[a]，arr[a] = b即可，即令1成为0的一个孩子
• 统计集合的个数：统计数组中元素为负数的个数

二、并查集的实现

#pragma once
#include<vector>
  #include<iostream>
    using namespace std;
    class UnionFindSet
    {
    public:
    UnionFindSet(int size)
    :_set(size, -1) // 初始时每个数据各是一棵树，元素均为-1
    { }
    // 查找一个数据属于哪个集合，找根元素的下标
    int FindRoot(int i)
    {
    while (_set[i] >= 0)
    {
    i = _set[i];
    }
    return i;
    }
    // 合并两个数据所在的集合
    void Union(int i1, int i2)
    {
    // 找这两个数据的根下标
    int root1 = FindRoot(i1);
    int root2 = FindRoot(i2);
    if (root1 != root2)
    {
    _set[root1] += _set[root2];
    _set[root2] = root1;
    }
    // 如果root1 == root2，说明这两个数据本就在一个集合，不用合并
    }
    // 判断两个数据是否在同一个集合
    bool IsSameSet(int i1, int i2)
    {
    return FindRoot(i1) == FindRoot(i2);
    }
    // 统计集合个数
    int SetCount()
    {
    int ret = 0;
    for (int n : _set)
    {
    if (n < 0)
    ret++;
    }
    return ret;
    }
    private:
    vector<int> _set;
      };

测试：

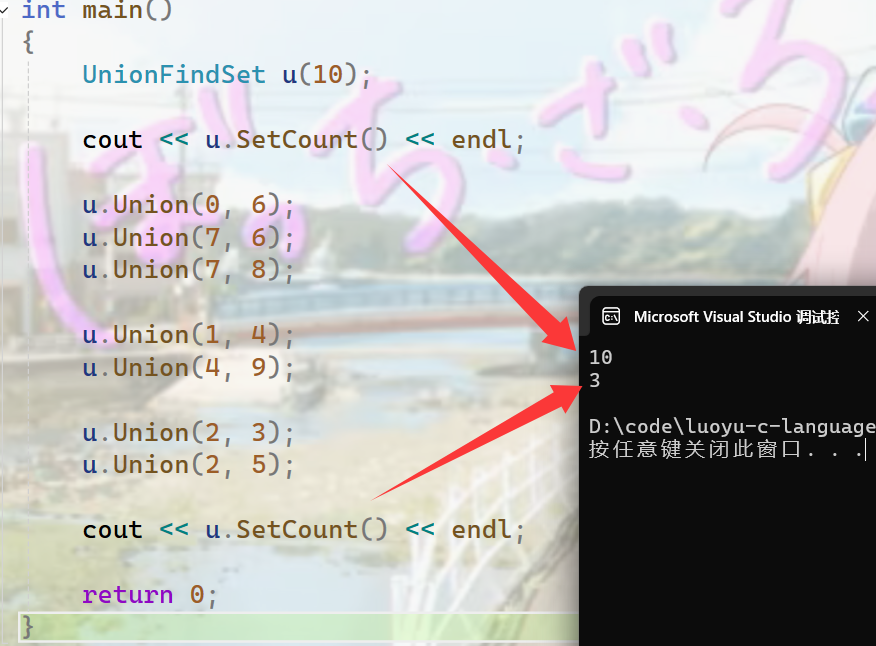
三、算法题中的应用

并查集的特点在某些算法题中很有用：

• 省份数量

class Solution {
public:
// 并查集, 统计集合数量
int findCircleNum(vector<vector<int>>& isConnected) {
  vector<int> ufs(isConnected.size(), -1);
    auto findRoot = [&ufs](int i)
    {
    while(ufs[i] >= 0)
    {
    i = ufs[i];
    }
    return i;
    };
    auto Union = [&ufs, &findRoot](int i1, int i2)
    {
    int root1 = findRoot(i1);
    int root2 = findRoot(i2);
    if(root1 != root2)
    {
    ufs[root1] += ufs[root2];
    ufs[root2] = root1;
    }
    };
    auto SetCount = [&ufs]()
    {
    int ret = 0;
    for(int n : ufs)
    {
    if(n < 0)
    ret++;
    }
    return ret;
    };
    for(int i = 0; i < isConnected.size(); i++)
    {
    for(int j = 0; j < isConnected[i].size(); j++)
    {
    if(isConnected[i][j] == 1)
    {
    Union(i, j);
    }
    }
    }
    return SetCount();
    }
    };

• 等式方程的可满足性

class Solution {
public:
// 并查集，数组大小26
// 遍历一次把所有==的两个字母放到一个集合，再遍历一次看!=的两个字符是否都在集合中出现过，出现过则false
bool equationsPossible(vector<string>& equations) {
  vector<int> ufs(26, -1);
    auto findRoot = [&ufs](int i)
    {
    while(ufs[i] >= 0)
    {
    i = ufs[i];
    }
    return i;
    };
    auto Union = [&ufs, &findRoot](int i1, int i2)
    {
    int root1 = findRoot(i1);
    int root2 = findRoot(i2);
    if(root1 != root2)
    {
    ufs[root1] += ufs[root2];
    ufs[root2] = root1;
    }
    };
    for(string& s : equations)
    {
    if(s[1] == '=')
    {
    Union(s[0]-'a', s[3]-'a');
    }
    }
    for(string& s : equations)
    {
    if(s[1] == '!')
    {
    int root1 = findRoot(s[0]-'a');
    int root2 = findRoot(s[3]-'a');
    if(root1 == root2)
    {
    return false;
    }
    }
    }
    return true;
    }
    };

本篇完，感谢阅读！