chns方程初了解（形式，求解内容，方式）

特性	不可压缩流	可压缩流
密度 (ρ)	常数(ρ = const)	变量(ρ = ρ(x, y, z, t))，随压力和温度变化
马赫数	Ma < 0.3 (约300 m/s以下，如水、低速空气)	Ma > 0.3 (如高速飞行、爆炸、内燃机)
能量方程	通常解耦，可先求解连续性+动量方程	强耦合，必须联立求解能量方程
物理现象	无激波、声波传播不是主要关注点	可能出现激波、膨胀波等复杂现象

2. ns方程形式

CHNS方程形式

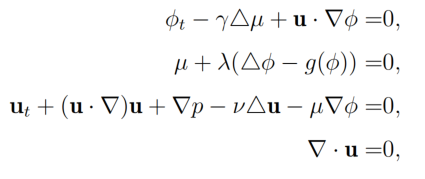
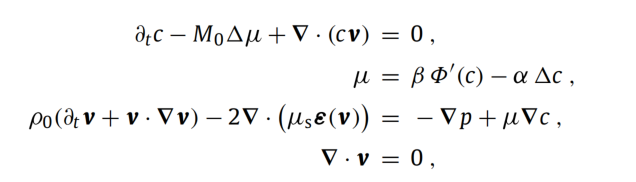
方程逐个对比分析

1. 第一个方程：演化方程

第一组 (1.1a):φ_t - γΔμ + u·∇φ = 0
第二组:∂_t c - M₀Δμ + ∇·(cv) = 0

差异原因：

变量不同：φ（相场）vs c（溶质浓度）
对流项形式不同：
- u·∇φ：相场被流体被动输运
- ∇·(cv)：溶质守恒输运（散度形式保证质量守恒）
物理意义：相场描述界面位置，浓度描述物质分布

2. 第二个方程：化学势定义

第一组 (1.1b):μ + λ(Δφ - g(φ)) = 0
第二组:μ = βΦ'(c) - αΔc

差异原因：

非线性程度不同：
- g(φ)：强非线性（如双阱势 φ³-φ）
- Φ'(c)：弱非线性（如二次函数）
梯度项系数不同：
- λΔφ：界面能项（抑制界面过薄）
- αΔc：扩散项（溶质的空间分布效应）
自由能泛函不同：相场用双阱势，溶质用混合自由能

3. 第三个方程：动量方程

第一组 (1.1c):u_t + (u·∇)u + ∇p - νΔu - μ∇φ = 0
第二组:ρ₀(∂_t v + v·∇v) - 2∇·(μₛε(v)) = -∇p + μ∇c

差异原因：

密度处理不同：
- 第一组：隐含ρ=1（无量纲化）
- 第二组：显式ρ₀（有量纲密度）
粘性项形式不同：
- νΔu：牛顿流体粘性（拉普拉斯形式）
- 2∇·(μₛε(v))：一般流体粘性（应变率张量形式）
驱动力不同：
- μ∇φ：表面张力驱动（界面力）
- μ∇c：浓度梯度驱动（溶质浮力）

4. 第四个方程：连续性方程

第一组 (1.1d):∇·u = 0
第二组:∇·v = 0

差异原因：

形式相同：都表示不可压缩条件
变量符号不同：u vs v（仅仅是符号选择）

形式差异的根本原因

1. 物理系统不同

复制

第一组：相分离系统
- 核心：界面演化
- 驱动力：表面张力最小化
第二组：溶质输运系统
- 核心：物质输运
- 驱动力：化学势梯度最小化

引用

2. 数学建模策略不同

方面	第一组	第二组
变量选择	相场φ	浓度c
自由能	双阱势	混合自由能
守恒律	界面守恒	质量守恒
耦合机制	界面-流体耦合	溶质-流体耦合

3. 数值处理需求不同

第一组需要处理：

界面锐化（保持界面厚度）
表面张力计算（曲率相关）

第二组需要处理：

浓度边界层
溶质守恒性

对研究的启示

方法选择：根据具体问题选择合适的CHNS形式
数值挑战：
- 相场CHNS：界面捕捉
- 溶质CHNS：浓度边界层处理
物理理解：不同形式反映不同的物理机制

此种形式差异体现了CHNS方程的灵活性和适应性——它可以根据具体物理问题调整数学形式，但保持核心的耦合思想。

CHNS求解多少个变量

最少需要求解 3 个核心变量，但完整的物理描述通常涉及5-7 个变量。

变量分层解析

第一层：核心求解变量（3个）

这些是必须通过求解PDE得到的未知函数：

变量	符号	物理意义	方程类型
相场	ϕϕ	相分布（0=流体A, 1=流体B）	Cahn-Hilliard方程
速度	u=(ux,uy,uz)u=(ux,uy,uz)	流体速度场	Navier-Stokes方程
压力	pp	压力场	连续性方程约束

注意：uu 是向量，在三维空间中涵盖3个分量，但通常被视为一个向量变量。

第二层：辅助变量（2个）

这些变量通常通过代数关系从核心变量导出，不直接求解PDE：

变量	符号	物理意义	定义方式
化学势	μμ	相变驱动力	μ=−λ(Δϕ−g(ϕ))μ=−λ(Δϕ−g(ϕ))
自由能密度	F(ϕ)F(ϕ)	热力学势	F(ϕ)=14ε2(1−ϕ2)2F(ϕ)=4ε21(1−ϕ2)2

第三层：物理参数（常量或已知函数）

这些是模型的输入参数，不是求解变量：

参数	符号	典型值/范围	物理意义
界面厚度	εε	10−8∼10−610−8∼10−6m	界面扩散尺度
混合能密度	λλ	材料相关	界面张力系数
运动粘度	νν	10−6∼10−310−6∼10−3m²/s	流体粘性
迁移率	γγ	10−12∼10−910−12∼10−9	相变动力学
密度	ρρ	103103 kg/m³	流体密度

CHNS方程数值手段全景图

我们可以将这些方法从三个维度进行分类：

时间离散策略(如何推进时间)
空间离散策略(如何处理空间)
体系耦合策略(如何处理变量间的耦合关系)

一、时间离散策略

这是决定格式精度和稳定性的核心。

1. 一阶格式

Euler 隐格式：
- 描述：最简单、最基础的隐式手段。
- 公式：un+1−unΔt=f(un+1)Δtun+1−un=f(un+1)
- 特点：无条件稳定（线性问题），但精度较低（O(Δt)O(Δt)）。
- 文献中出现：Feng [29], Diegel et al. [22]

2. 二阶格式

时间二阶格式：
- 描述精度与效率的平衡点。就是：精度更高（O(Δt2)O(Δt2)），
- 常见实现：Crank-Nicolson, BDF2等。
- 特点：计算成本适中，稳定性好，是工业和学术研究的主流选择。
- 文献中出现：Han & Wang [41], Diegel et al. [23]

二、空间离散策略

这首要指有限元方法中的具体技术。

1. 混合有限元方法

描述：使用多个不同的有限元空间来求解耦合问题。
核心应用：处理Navier-Stokes方程中的速度-压力耦合。
原因：速度和压力的有限元空间需要满足特定的inf-sup条件（或LBB条件），以避免数值不稳定（如压力振荡）。
文献中出现：几乎所有文献都隐含或明确采用了该手段，如Feng [29], Diegel et al. [22, 23]。

2. 稳定化方法

描述：依据添加小的稳定项，使得inf-sup条件不再被严格要求，允许使用更简单的、等阶的速度-压力有限元空间。
优点：增加了有限元空间选择的灵活性，简化了程序实现。
文献中出现：Shen & Yang [69, 70], Cai & Shen [14], Chen et al. [18]。

三、系统耦合策略

这是处理CHNS强非线性和复杂耦合的关键，也是算法创新最活跃的领域。

1. 全耦合格式

描述：将相场、化学势、速度、压力等所有变量放在一个大的非线性框架中，同时求解。
优点：物理上最忠实于原方程，耦合紧密。
缺点：系统规模巨大，求解困难，计算成本极高。
文献中出现：Grün [36], Shen & Yang [69]。

2. 解耦格式

研究的重点和难点，旨在将大系统拆分为若干个小环境，提高计算效率。就是这

a) 弱耦合格式

描述：系统被拆分，但各子系统的求解仍需在单个时间步内进行迭代，直至收敛。
特点：介于全耦合和完全解耦之间，计算量和耦合度居中。
文献中出现：Cai & Shen [14]。

b) 完全解耦格式

描述：将大体系拆分为多个独立的子系统，每个子系统可以顺序、独立地求解，无需迭代。
优点：计算效率最高，易于并行化。
缺点：设计难度大，需要巧妙地处理耦合项以保证稳定性和精度。
文献中出现：Shen & Yang [70], Xu et al. [76], Chen et al. [18]。

️ 四、核心构造手艺

为了达成上述的解耦和稳定性，研究者们发明了一些巧妙的技术。

1. 凸分裂方法

描述：将自由能泛函 F(ϕ)F(ϕ) 人为地分裂成一个凸的部分 Fc(ϕ)Fc(ϕ) 和一个凹的部分 Fe(ϕ)Fe(ϕ)，即 F(ϕ)=Fc(ϕ)+Fe(ϕ)F(ϕ)=Fc(ϕ)+Fe(ϕ)。
作用：对凸部分进行隐式处理，对凹部分进行显式处理，从而既能保证能量稳定性，又能避免完全隐式的非线性求解。
文献中出现：Shen & Yang [70], Han & Wang [41], Diegel et al. [22]。

2. 压力投影法

描述：一种经典的处理不可压缩流的方法，将速度和压力的求解分离开。
步骤：
1. 先求解一个不含压力梯度的“中间速度”。
2. 再依据求解一个压力泊松方程来修正中间速度，使其满足不可压缩条件。
优点：避免了直接求解速度-压力的鞍点问题。
文献中出现：Han & Wang [41], Chen et al. [18]。

五、分析目标

文献中反复提到的研究目标，反映了该领域的关注重点。

1. 能量稳定性

目标：证明数值格式的离散能量随时间单调不增，即 En+1≤EnEn+1≤En。
类型：
- 条件稳定：对时间步长 ΔtΔt 有要求。
- 无条件稳定：对 ΔtΔt 没有限制。
文献中出现：几乎所有文献都提到了这一点。

2. 误差估计

目标：从数学上严格证明数值解与精确解之间的误差，给出收敛阶。
难点：CHNS的强非线性和复杂耦合使得误差分析非常困难。
类型：
- 半离散误差估计：只分析空间离散误差。
- 全离散误差估计：同时分析空间和时间离散误差（更难，成果更少）。
文献中出现：Feng [29], Diegel et al. [22, 23], Cai & Shen [14], Xu et al. [76], Chen et al. [18]。

总结表格

方法类别	具体方法	主要特点	代表文献
时间离散	Euler隐格式	一阶，无条件稳定	Feng [29], Diegel [22]
	时间二阶格式	二阶，精度与效率平衡	Han & Wang [41], Diegel [23]
空间离散	混合有限元	处理速度-压力耦合	几乎所有
	稳定化方法	放宽inf-sup条件	Shen & Yang [70], Cai & Shen [14]
系统耦合	全耦合	精确，计算昂贵	Grün [36]
	弱耦合	迭代求解，折中方案	Cai & Shen [14]
	完全解耦	高效，线性求解	Shen & Yang [70], Xu [76]
构造技术	凸分裂	保证能量稳定性的关键	Shen & Yang [70], Han & Wang [41]
	压力投影法	分离速度和压力	Han & Wang [41], Chen [18]
分析目标	能量稳定性	保证物理合理性	几乎所有
	误差估计	验证数学收敛性	Feng [29], Diegel [23]

这段综述清晰地展示了CHNS数值方法从“能算”（建立格式、证明稳定）到“算好”（解耦、线性化、高效）再到“算准”（严格的误差分析）的发展历程。

posted on 2026-01-10 16:01 ljbguanli 阅读(13) 评论(0) 收藏举报