详细介绍：【机器学习】10 正则化 - 减小过拟合

10 Regularization to Reduce Overfitting

10.1 The Problem of Overfitting

通过过拟合 Overfitting，通常也能够描述为 High Variance （高方差）
欠拟合 Underfitting，通常也可以描述为 High Bias （但该词也有很多别的用法）

正则化 Regularization 是常用的缓解过拟合挑战的方法
泛化 Generalization 指模型在没见过的新的例子上也能表现良好的能力
过拟合的例子（泛化能力差）：

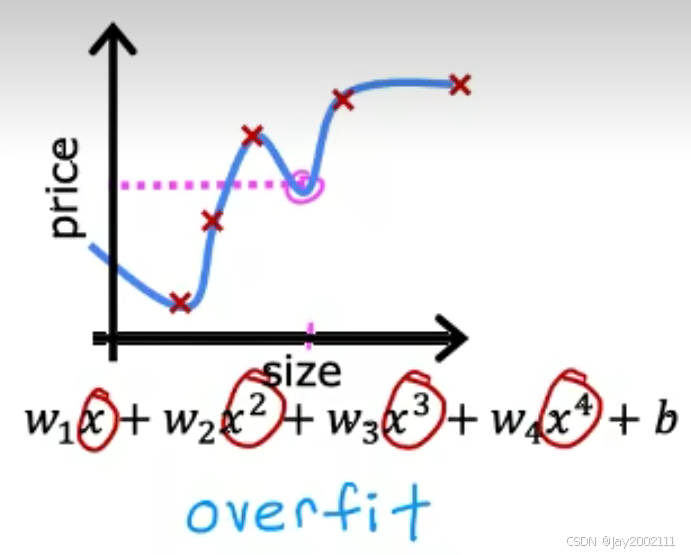
10.2 解决过拟合 Addressing Overfitting

1. 收集更多的训练数据
2. 考虑启用更少的特征，最合适的特征
   通常，特征数量少于合理值导致欠拟合，特征数量多于合理值导致过拟合
   要选择最合理的特征，泛化强的特征 -->Feature Selection
3. 正则化 Regularization
   减少过大的特征参数权重$w_j$，防止某一特征产生过大的影响
   与策略2去除特征类似，但是更温和，不是完全把$w_j$置0

注：一般只正则化w，而参数b是否正则化通常不会造成很大影响
总结一下：

10.3 Cost Function with Regularization

可以让成本函数加上若干倍想降低的$w_j$的平方：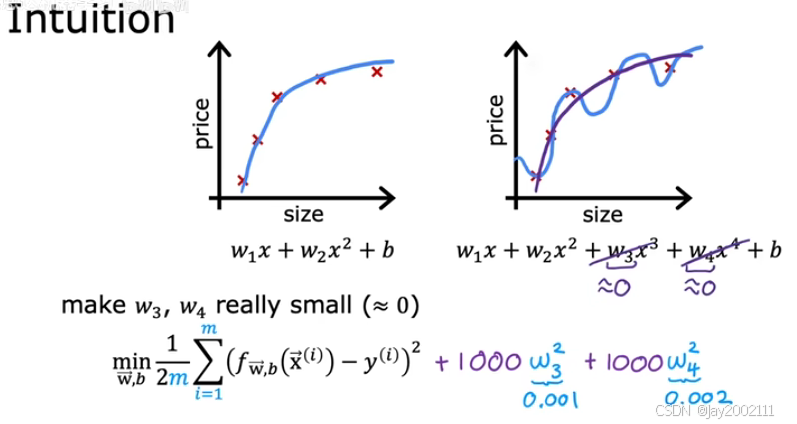

但大多数情况下，特征很多，我们也并不知道哪些特征要被弱化/惩罚
所以，对所有$w_j$都这样运行正则化，缩小所有$w_j$，行得到一个更平滑的函数，不容易过拟合

注：大多数情况下，参数b是否正则化影响并不大，所以一般不必对b进行正则化

现在，我们记m代表有m个训练样本，n代表有n个特征，那么，我们有：
$$J(\vec{w},b)=\frac{1}{2m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)}{)}^2+\lambda \sum _{j=1}^n{w}_j^2$$

但是通常我们会将$\lambda$也进行$\frac{1}{2m}$的缩放，事实证明这样管理的话，$\lambda$的取值在m增大，即训练集规模增大的同样表现良好：
$$J(\vec{w},b)=\frac{1}{2m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)}{)}^2+\frac{\lambda }{2m}\sum _{j=1}^n{w}_j^2$$

注：

1. 这里的$\lambda$称作 正则化参数（Regularization Parameter），类似学习率$\alpha$，也是一个需要确定的超参数
2. 现在我们的目标是最小化$J(\vec{w},b)$，它由两项组成，前者是均方误差（Mean Squared Error，MSE），后者是正则化项（Regularization Term），而$\lambda$描述了对两者之间的重要性的权衡，前者鼓励算法的预测值更贴近训练集的真实值，而后者鼓励算法减小w而减少过拟合
3. 极端情况：要是$\lambda$置0，那么完全没有正则化项，预测函数可能过拟合得非常严重；倘若$\lambda$置为一个极大的数，那么以线性回归为例，所有的w为了满足使正则化项变小，w将会变得趋于0，那么只剩下b，预测函数将会趋于直线b，严重欠拟合。所以，$\lambda$的值控制了模型过拟合和欠拟合的平衡

10.4 Regularized Linear Regression

回顾之前的线性回归梯度下降公式：
$$\begin{gathered} w_j=w_j-\alpha \frac{\partial }{\partial w_j}J(\vec{w},b) \\ b=b-\alpha \frac{\partial }{\partial b}J(\vec{w},b) \end{gathered}$$

添加正则化项的情况下不难发现，b的表达式并不会变化，因为我们没有对b正则化。w的表达式，正则化项会引入一个新的导数项，那么有：
$$\begin{gathered} \frac{\partial }{\partial w_j}J(\vec{w},b)=\frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda }{m}{w}_j \\ \frac{\partial }{\partial b}J(\vec{w},b)=\frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)}) \end{gathered}$$

完整地写出来：
$$\begin{gathered} w_j=w_j-\alpha [\frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda }{m}{w}_j] \\ b=b-\alpha \frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)}) \end{gathered}$$

我们把关于$w_j$的式子改写一下：
$$w_j=w_j(1-\alpha \frac{\lambda }{m})-\alpha \frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)})x_j^{(i)}$$

后一项与不带正则化项的梯度下降一致，唯一的区别在于$w_j$在更新中不断缩小（$1-\alpha \frac{\lambda }{m}$是一个略小于1的数值）

10.5 Regularized Logistic Regression

和不带正则化的逻辑回归类似，带正则化的逻辑回归的梯度下降也与线性回归的表达式看起来类似，但同样需要注意，里面的$f_{\vec{w},b}(\vec{x})$不一样。
$$\begin{gathered} w_j=w_j(1-\alpha \frac{\lambda }{m})-\alpha \frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}(x^{(i)})-y^{(i)})x_j^{(i)} \\ b=b-\alpha \frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}(x^{(i)})-y^{(i)}) \end{gathered}$$