实用指南：【论文阅读】Gradient-free Decoder Inversion in Latent Diffusion Models

NeurIPS 2024paper：https://proceedings.neurips.cc/paper_files/paper/2024/file/970f59b22f4c72aec75174aae63c7459-Paper-Conference.pdf

code：https://smhongok.github.io/dec-inv.html

abstract

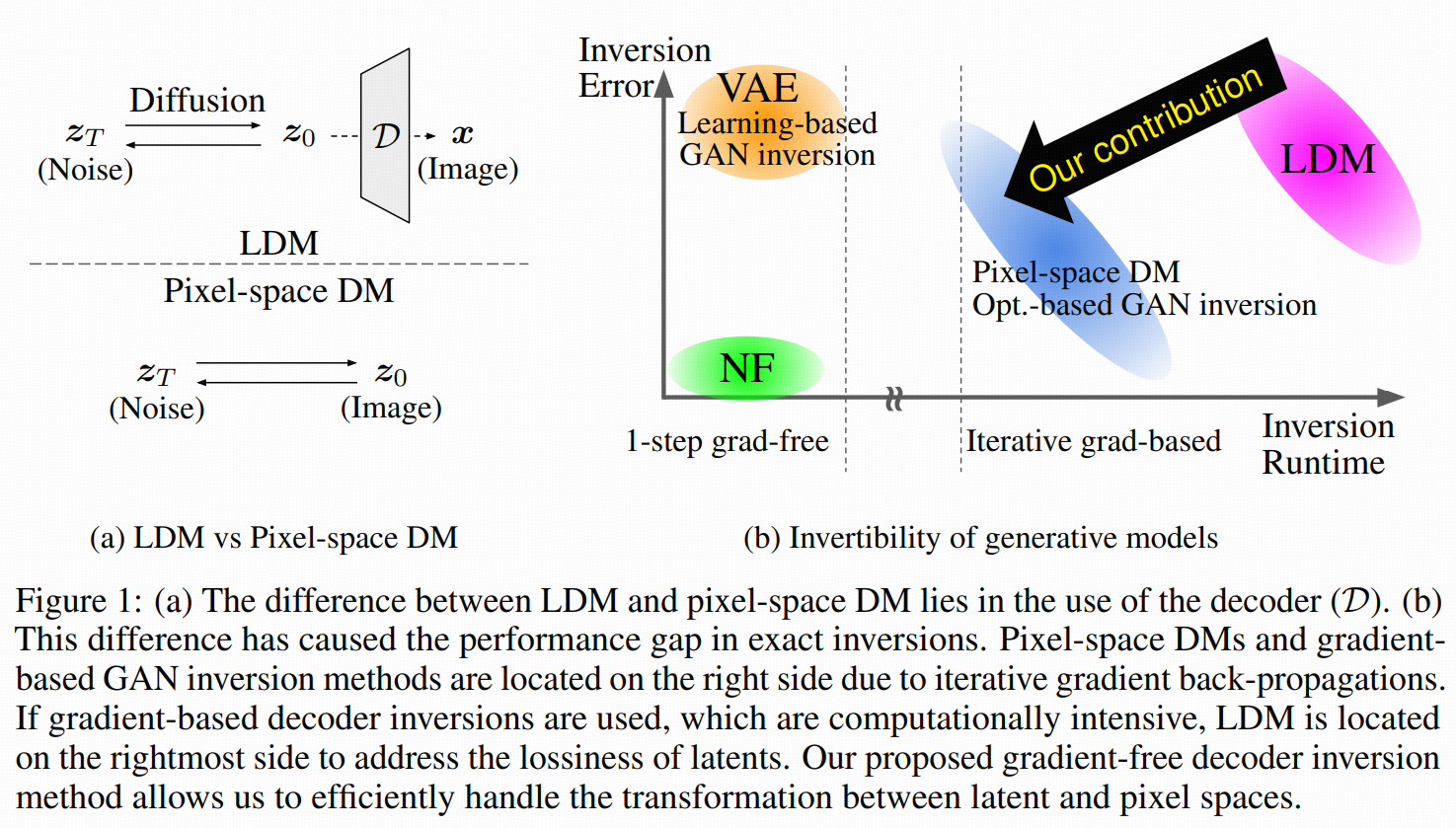
这篇文章关注的是潜空间扩散模型（LDM）里的解码器反演障碍。核心背景：

• 在 LDM 里，扩散是在低维 latent 空间 z 做的，最后凭借 decoder D 把 z 变回像素空间 x。

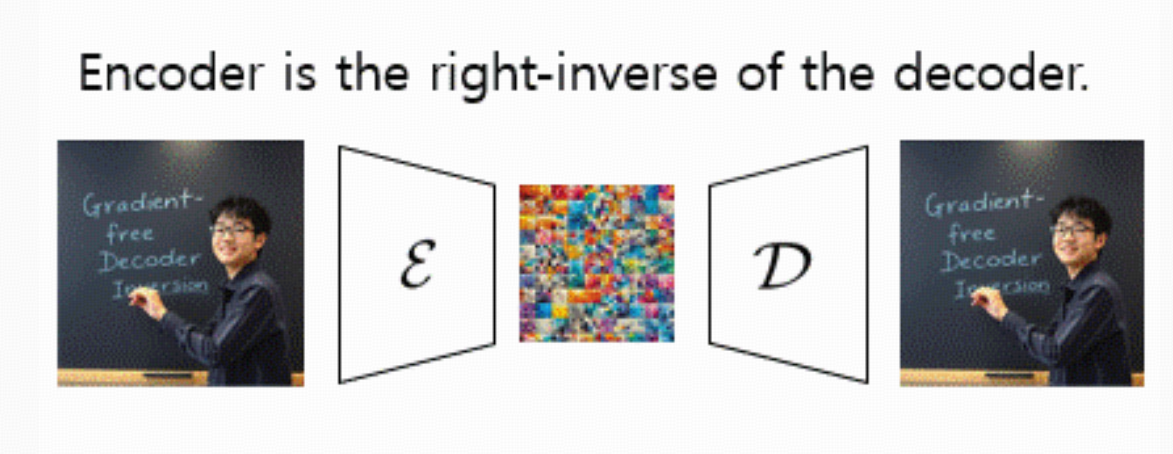
• 理想状态：有一个 encoder E，它是 decoder 的精确逆：

  • 右逆：D(E(x))≈x （重建像素）

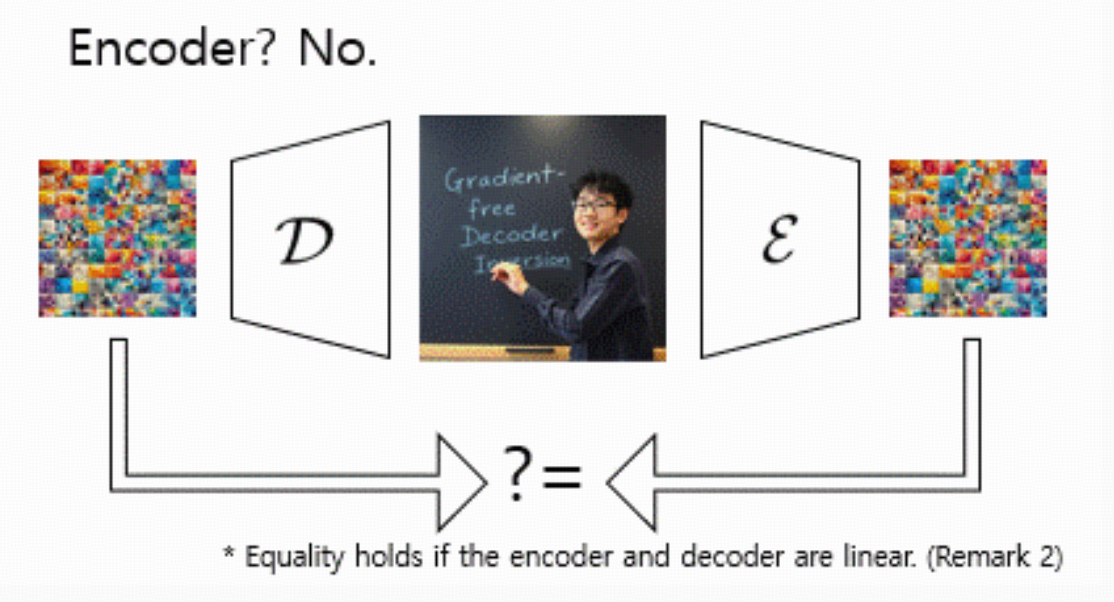
  • 左逆：E(D(z))≈z（保持 latent）

• 现实中：只保证右逆（重建好看），左逆往往并不成立。这就导致：

  • 给定一张真实图像 x，你想找到一个 latent z 满足 D(z)≈x，这个“decoder 反演”通常做得不够好。

以前的做法：

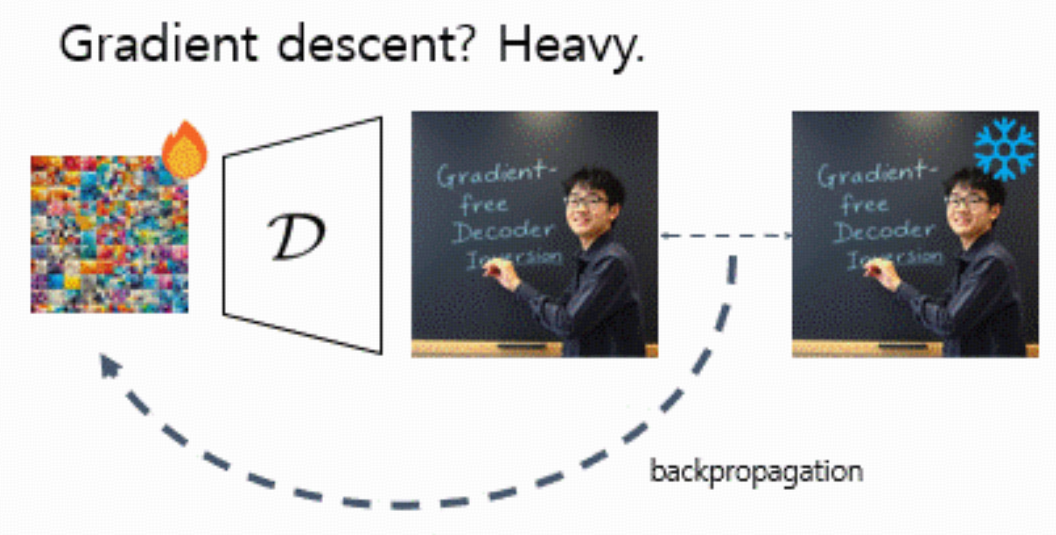
• 直接把 decoder D 当成 GAN 的 generator，用梯度下降优化 latent：min⁡zℓ(x,D(z))

• 得对 D 反向传播，显存和算力都很吃紧。尤其是视频 LDM，一次生成十几帧甚至几十帧时，gradient-based inversion 几乎跑不动。

这篇工作提出：

1. 一个完全不需要梯度的 decoder inversion 算法（gradient-free）：

   • 只调用 E 和 D，不对 D 做 backward。

2. 在一个很温和的假设（cocoercivity 共压缩性）下，给出严格的收敛证明，包括：

   • 朴素 forward step method

   • 带动量的 inertial Krasnoselskii-Mann (KM) 迭代

3. 结合 Adam 和学习率调度，实验证明：

   • 最多 5× 更快

   • 最多省 89% 显存

   • 还能用 FP16 跑，但梯度法在 FP16 会 underflow。

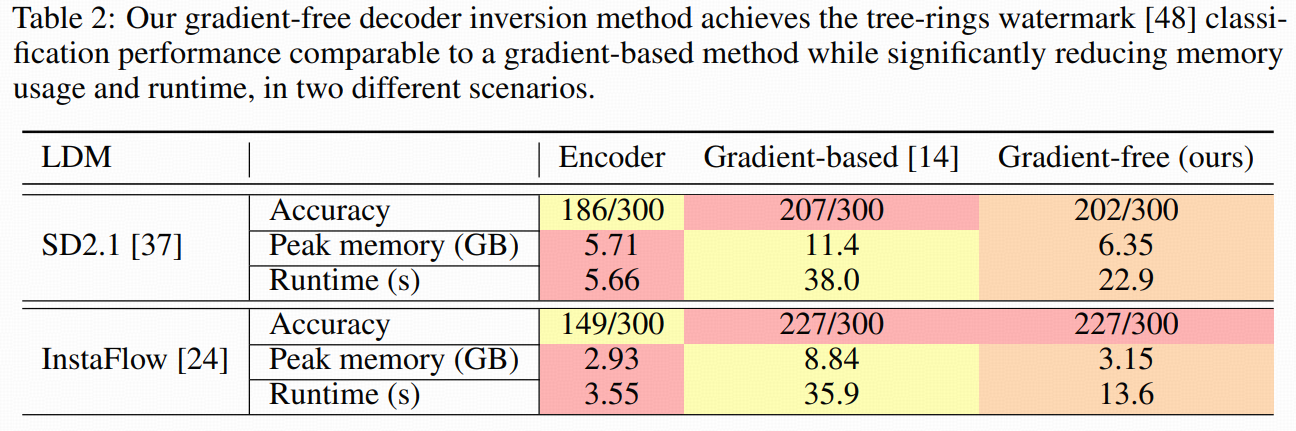
4. 应用上，在噪声空间水印（tree-ring watermark）检测和背景保持的图像编辑里，达到了和梯度方法相近的误差水平，但大幅节省时间和内存。

主页的动图讲解：

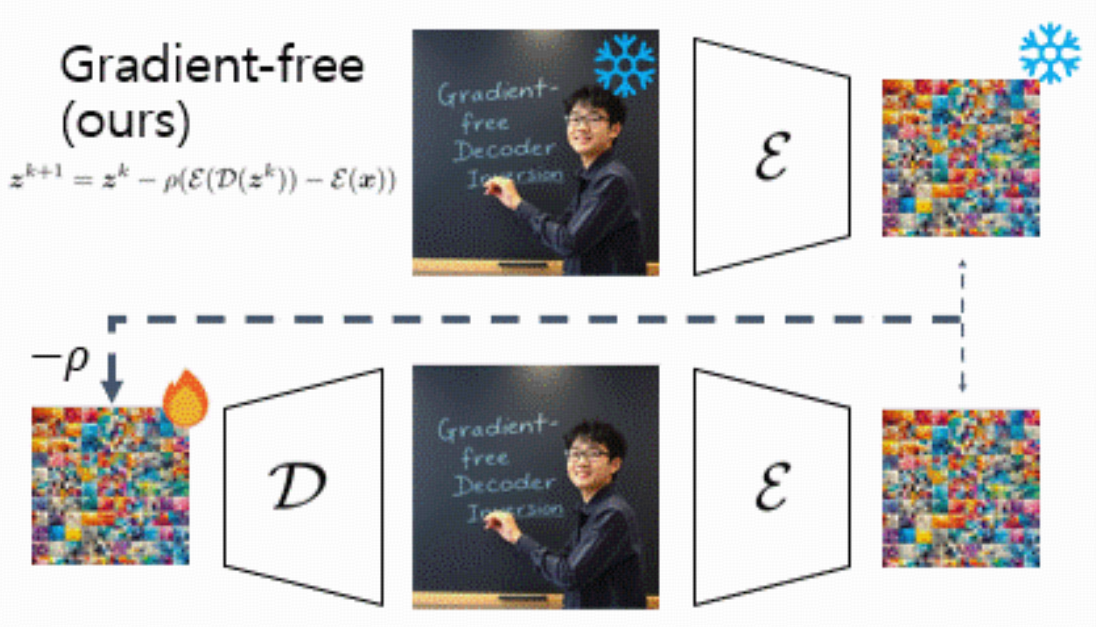
Backgrounds

2.1 Latent diffusion models (LDMs)

这里就是点名了几种他们实验中用的 LDM：

• Stable Diffusion 2.1：text-to-image LDM。

• LaVie：cascade video LDM（多级 latent）。

• InstaFlow：one-step text-to-image 模型。

额外强调一点：

除了 latent 这种“有损压缩”会破坏可逆性，加速采样（高阶 ODE solver）也让扩散反演更难。比如 DPM-Solver 的反向并不是简单的把 steps 倒过来。

2.2 Optimization-based GAN inversion

经典 optimization-based GAN inversion 就是：min ⁡z ℓ(x,G(z))

• G：GAN 的 generator

• ℓ：图像距离度量（ℓ2\​、感知 loss 等）

• 算法：对 z 做梯度下降（L-BFGS、Adam 等）。

常见技巧两种：

1. (A) 用 encoder 初始化：

   • 先训练一个 encoder E，输出 E(x))，作为优化初值 z0=E(x)。

2. (B) 用 encoder 做正则：

   • 约束 z 留在 encoder 的流形附近：

     

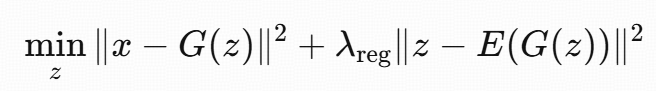
本文也会用 (A)，但不会像 (B) 那样把 encoder 仅仅当 regularizer，而是把它直接塞进迭代算子里当“伪梯度”。

2.3 Gradient-based decoder inversion in LDMs

LDM 的 decoder inversion 直接照搬 Eq.(1)：

min⁡zℓ(x,D(z))

梯度下降：

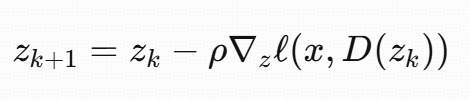
问题：

• 每次迭代都要算 ∇zD(zk)（整个 decoder 的 backward）。

• 对大模型 / 视频 LDM 来说，显存和时间都扛不住。

这就是本文想要替代的对象。

method

3.1 Motivation

（动机：从 x=D(z) 到 E(x)=E(D(z))）

理想的 decoder inversion 目标：find z∈RF x=D(z)

问题在于：

• D 是有损解码器，甚至多对一，很可能没有严格解；

• 就算有，直接解这个等式也没现成的结构可用。

所以作者提出：退一步，只要求 E(x)=E(D(z))

直觉：

• encoder E 把像素投到 latent 空间；

• 假设 E,DE 接近一个 autoencoder 的关系，那么要求 ED(z) 和 E(x)相等，比直接要求 D(z)=x要容易很多。

论文里的 Remark 1 写的是集合包含关系：

3.2 Convergence analysis on forward step method

（前向迭代的收敛）

他们把算子记作：

3.3 Convergence analysis on momentum for acceleration

为了加速，他们不满足于简单的 forward step method，而是用惯性 Krasnoselskii-Mann (KM) 迭代：

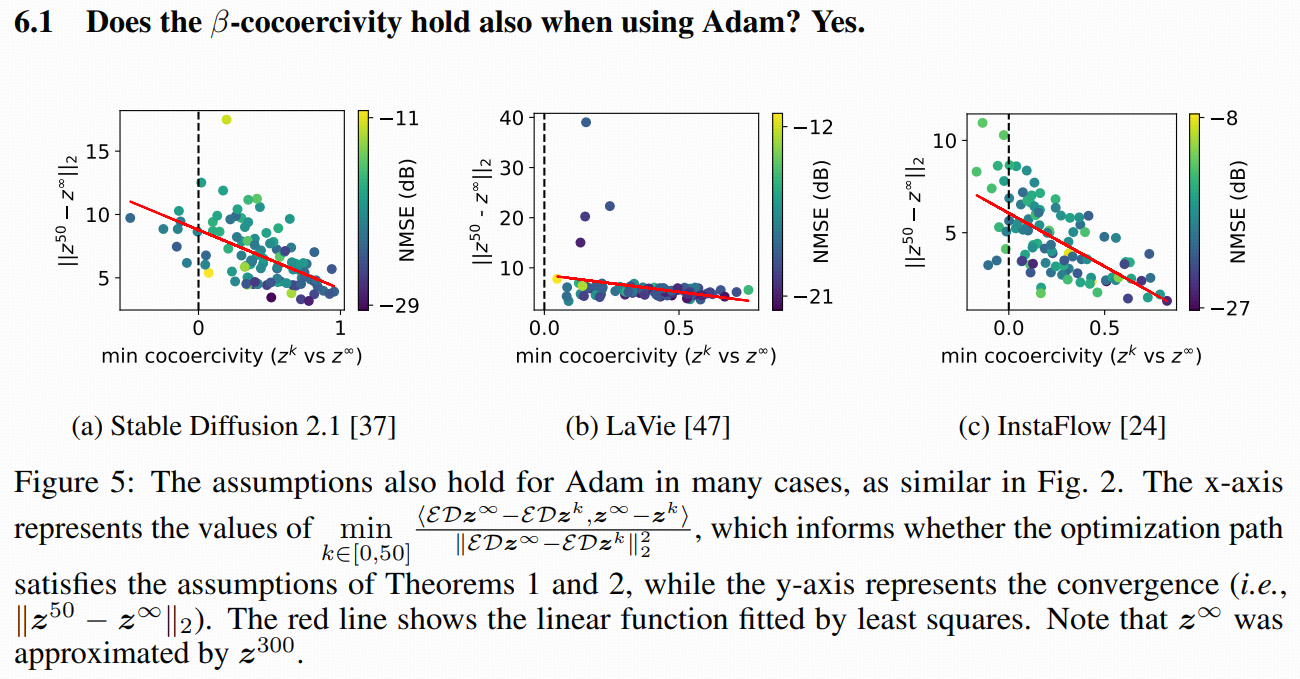
3.4 Validation of the assumption

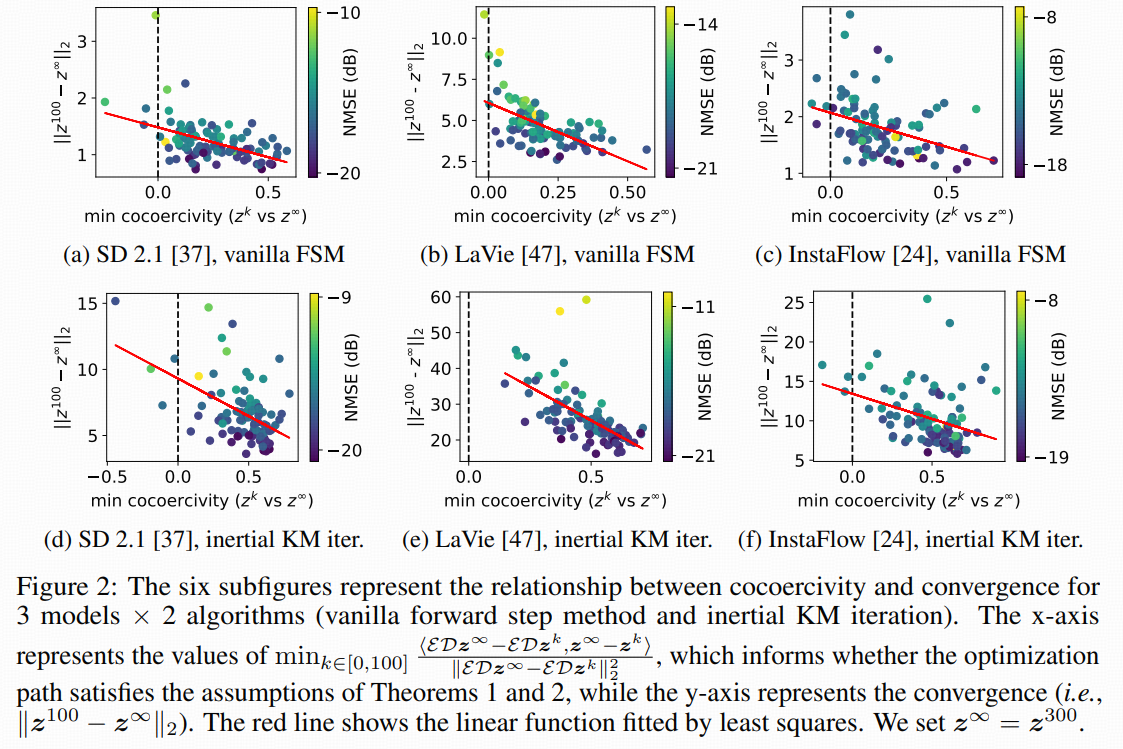
4 Experiments with practical optimization techniques

4.1 Adam optimizer

他们在这里没再做理论证明，而是直接用 Adam 来更新：

• 把 gk=T(zk)=E(D(zk))−E(x) 当作“梯度”；

• 喂给 Adam，按标准 Adam 公式更新 zk。

关键区别：

• 仍然不需要对 D 反向传播；

• Adam 会自动做 per-dim 自适应步长，比固定 ρ 收敛更快，抖动更小。

4.2 Learning rate scheduling

他们用的是类似 [14] 的策略：

• 总步数为 T，

  • 前 1/10 步：线性 warmup 到 peak lr；

  • 中间 7/10 步：cosine decay；

  • 最终 2/10 步：lr 固定。

这样不管总迭代是 20、50 还是 200，都有比较平滑的 lr schedule。

4.3 实验对比结果（和梯度法的真正差距）

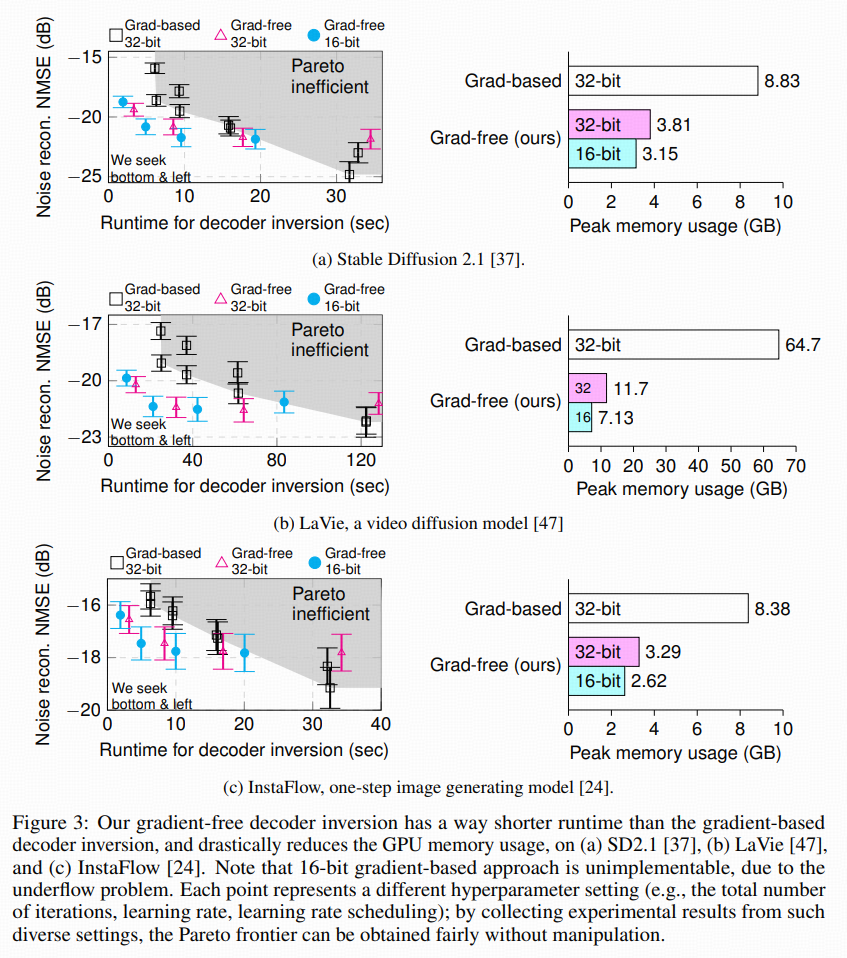
Figure 3 是这篇文章非常关键的一张图：

• 三个模型：SD2.1、LaVie（视频）、InstaFlow（one-step）

• 横轴：运行时间 / 峰值显存

• 纵轴：inversion NMSE（dB）

• 每个点：一种超参组合（总迭代数、lr、scheduler 是否开启、位宽 16/32 等）。

• 从众多点里画出各自的 Pareto frontier，对比：

  • gradient-based 32-bit

  • gradient-free 32-bit

  • gradient-free 16-bit

结论非常清晰：

• 速度：在达到同样误差时，gradient-free 最多可快5×；

• 显存：视频 LDM 上最多省89%（64.7GB → 7.13GB）；

• 精度：在给定时间预算下，gradient-free 的最优点比梯度法低约 2.3 dB（误差更小）；

• 位宽：梯度法 16-bit 会 underflow，根本跑不起来；

  • 通过gradient-free 因为没有 backward，能够全程 16-bit，很稳。

总结