完整教程:[GNN图神经网络零基础论文精读]A Gentle Introduction to Graph Neural Networks
原论文(博客)发表在Distill上,链接如下:
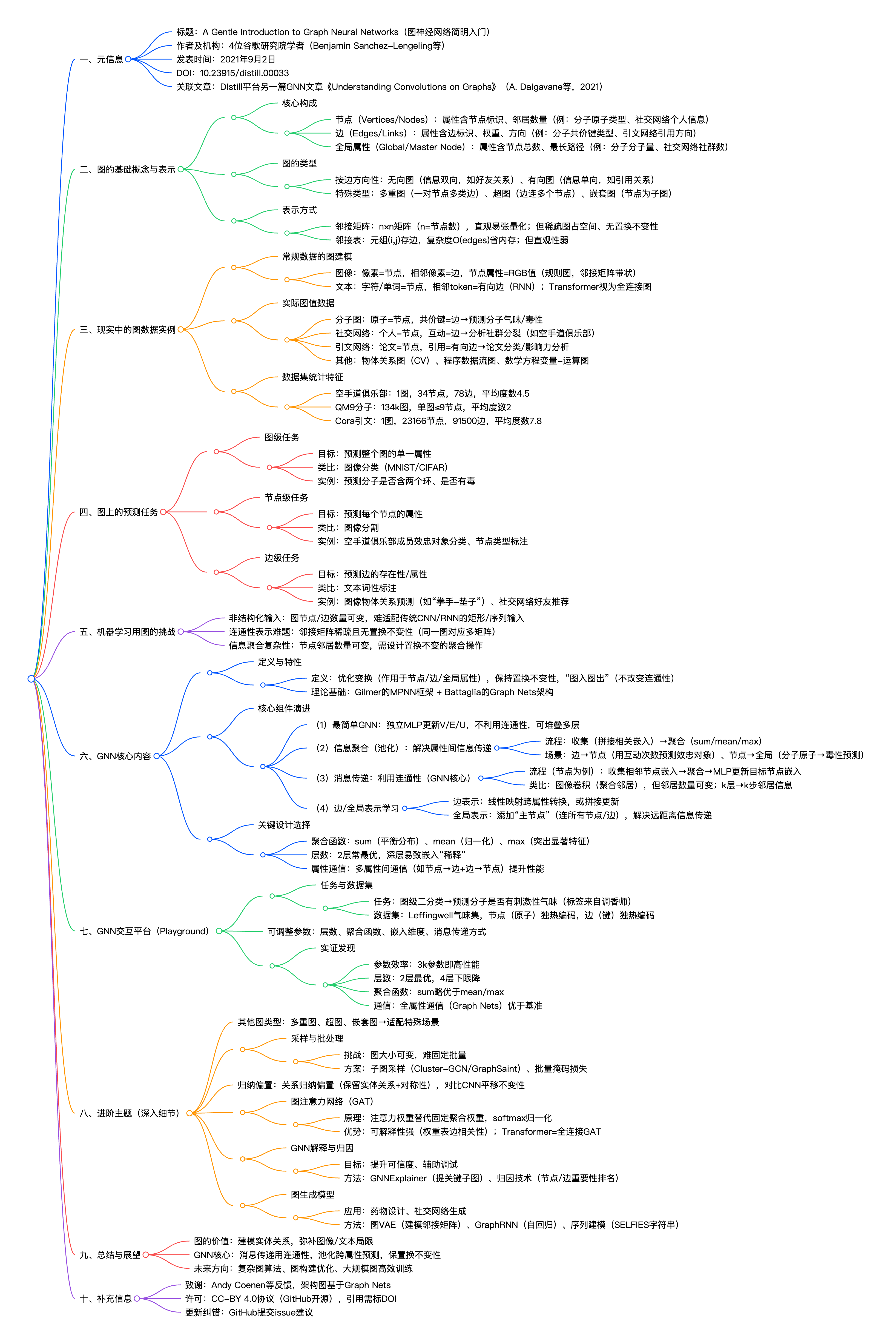
我们将原论文的思维导图放在了文章的末了,也在最后留了一个彩蛋!!!
目录
(2) 信息聚合(池化)—— 解除 “属性间信息传递” 问题
Learning edge representations 学习边表示
Adding global representations 添加全局表征
一.前言——为什么这篇文章值得所有人读
1.GNN在生活中的应用场景
(1) Q : 为什么某 APP 总能推荐你想认识的朋友?
A : 社交网络 “好友推荐”——GNN 的边级任务)
(2) Q : 科学家怎么快速找到可能治新冠的分子?
A : 分子毒性预测 ——GNN 的图级任务
(3) Q : 某平台怎么判断这篇论文属于 AI 领域?
A : 引文网络论文分类 ——GNN 的节点级任务
2.本篇论文的学术地位
作者是谷歌研究院团队,发表在顶刊级平台 Distill,全文无晦涩公式堆砌,全是 “人话 + 动态图”
3.读完博客你或许会收获
从零基础到技术拆解,再到学术进阶的“挖坟式”写作方式,带你搞懂手撕GNN!!!
二、图的基本概念和表示(GNN的前置知识)
1.前人的定义
Franco Scarselli等人在《The Graph Neural Network Model》当中给图下的定义为:
"A graph is a structure composed of a set of nodes V and a set of edges E⊆V×V, where each node can carry attributes and edges can be labeled with weights or types."
2.“图”究竟是什么?
(1) 图的核心构成
图由节点(Vertices/Nodes)、边(Edges/Links) 和全局属性(Global/Master Node Attributes)组成,各组件可存储标量或嵌入向量形式的信息:
- 节点属性:如节点标识、邻居数量(例:分子中的原子类型、社交网络中的个人信息);
- 边属性:如边标识、边权重、方向(例:分子中的共价键类型、引文网络中的引用关系方向);
- 全局属性:如图的节点总数、最长路径(例:分子的分子量、社交网络的社群数量)
(2) 图的分类
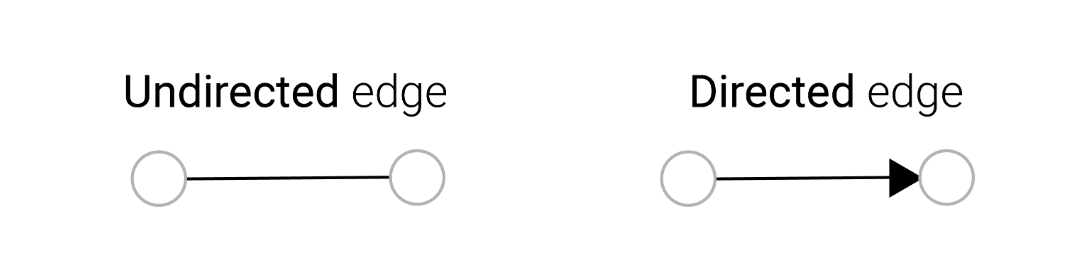
无向图(Undirected edge):两个顶点之间的“边”是没有方向的,就好比微信当中,你是我的朋友,所以我也是你的朋友(当然是在没有被拉黑的情况下)
有向图(Directed edge):两个顶点之间的“边”是有方向的。比如说在抖音或BiliBili这样的平台,我关注了迪丽热巴,但是迪丽热巴未必会关注我,这时我们两个之间的图就是有向图。或者说论文的引用,一般没有两篇文章相互引用的情况,更多的是后人的文章引用前人的研究结果
特殊图类型:多重图,超图
(3) 图的表示方式
| 表示方式 | 原理 | 优势 | 缺点 |
|---|---|---|---|
| 邻接矩阵 | 用n×n矩阵(n 为节点数)表示节点连通性,矩阵元素标识边是否存在 / 权重 | 易于张量化,直观 | 稀疏图空间效率低;不具备置换不变性,同一图可对应多个矩阵 |
| 邻接表 | 用元组(i,j)存储边的连接关系,仅记录存在的边 | 节省内存 | 直观性弱 |
三、图上的预测任务(GNN要解决什么样的问题)
图里面的任务首要分为三大类:
图级、节点级和边级。
- 对于节点级任务,我们预测图中每个节点的属性。
- 对于边级任务,我们预测图中边的属性或者是否存在这条边。
- 对于图级任务,我们预测整个图的属性。
在这篇文章当中,给出了如下的例子,也就是我们希望GNN能够处理什么样的困难。
四、图数据的实例
1. 常规数据的图
Images as graphs 图像即图规则结构的图,邻接矩阵呈带状);就是:像素为节点,相邻像素(如 8 邻域)为边,节点属性为 RGB 值(本质
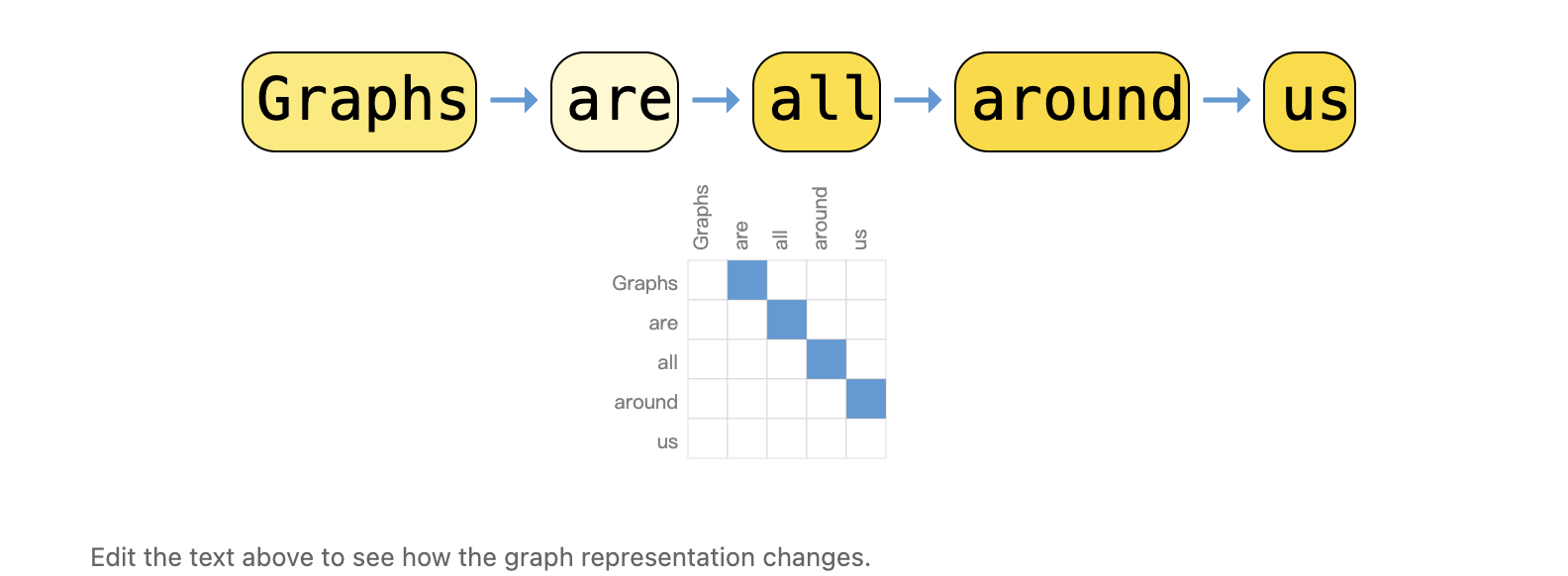
Text as graphs 文本即图:字符或者单词为节点,相邻 token 为有向边,RNN 的序列表示);Transformer 则将文本视为全连接图,学习 token 间关系。
我们可以通过为每个字符、单词或标记分配索引,并将文本表示为这些索引的序列来将文本数字化。这会创建一个容易的有向图,其中每个字符或索引都是一个节点,并利用一条边连接到其后的节点。
2. 实际图值数据
- 分子图:原子为节点,共价键为边,用于预测分子气味、毒性等;
- 社交网络:个人为节点,互动关系为边,用于分析社群分裂、成员效忠关系;
- 引文网络:论文为节点,引用关系为有向边,用于论文分类、影响力分析;
- 其他:计算机视觉中的物体关系图、程序代码的数据流图、数学方程的变量 - 运算图。
3. 图数据集统计特征
不同领域图的节点数、边数、节点度数差异极大。
五、机器学习当中应用图的挑战(challenge)
这部分内容,大家将按照例子引入的通俗解释,然后逐渐加深理解。
| 挑战 | 核心矛盾(零基础总结) | GNN 的解决思路(学术呼应) |
|---|---|---|
| 非结构化输入 | 图没有固定格式,传统模型要 “标准箱子” | 设计 “图入图出” 架构,用嵌入层适配变长节点 / 边属性 |
| 连通性表示难题 | 节点排序变了,图没变,但传统模型认不出 | 保持 “置换不变性”,让模型忽略节点顺序,只关注关系 |
| 信息聚合复杂性 | 节点邻居数量不一样,传统聚合 “模板不通用” | 用 sum/mean/max 等置换不变聚合函数,适配可变邻居集 |
这部分是在对之前的文献提出问题,在机器学习当中图面临的挑战有哪些?以及大家为什么要使用GNN。
具体内容如下:
1. 非结构化输入
假设你现在要寄快递,快递员给了你一个正方形的箱子
如果你寄的是书,排列整齐,恰好能装进箱子
如果你寄的是一捆一捆的线绳,也能卷成固定的体积塞进箱子里面
这里所提到的“正方形的箱子”也就是先前AI大模型的输入格式。
比如说卷积神经网络CNN(Convolutional Neural Network),循环神经网络RNN(Recurrent Neural Network)都有其对应的输入格式:
- CNN 需要 “矩形输入”,如 224×224 的图片;
- RNN 需要 “固定长度的序列”,如 100 个单词的句子;
而图的节点数、边数是 “随心所欲” 的:
比如分子图有的含 5 个原子(5 节点),有的含 20 个;社交网络图有的 10 个用户,有的 10 万用户 —— 此种 “没有固定格式的输入”,传统模型接不住。
传统 AI 模型的 “输入层设计” 是 “固定维度” 的,无法适配图的 “变长特性”。
现在我们假设,图神经网络GNN能够照搬CNN或RNN的思路:
- 假设用 CNN 处理 “分子图”,CNN 的卷积核需要 “像素排列成网格”,但分子中原子的连接是 “不规则的”,比如 C 原子可能连 2 个 H,也可能连 3 个 O,没有 网格结构,卷积核不知道该 “扫哪里”,自然无法提取特征。
- 假设用 RNN 处理 “社交网络图”,RNN 需要 “序列顺序”,但社交网络中 好友关系是无顺序的,强行按顺序输入 RNN,会让模型误以为 “顺序有意义”,导致预测错误。
那我现在要如何去应对这样的问题呢?
模型设计的痛点——变长输入处理问题!!!
图的本质是“无序集合”,既然是无序的,那么节点的排序根本就不会影响边的关系。
但传统模型输入的是有序的张量,任意一个维度的顺序改变了都可能导致报错。
那么现在需解决的难题就十分清楚明确了——就是要设计出来一个模型,解决“变长输入处理问题”。后来的GNN就是借助“置换不变性”来解决了这样的难题。
即,不管节点怎么排序,输出都是不变的。
如何达成呢?背后的数学原理是什么呢?
我们需要找到对于元素顺序不敏感的函数!
集合论中的对称函数”(sum/mean/max等)
2. 联通性表示
老师,想记录 “班级同学的好友关系”:就是假设你
你画了一张 “座位表”:座位 1 的同学和座位 2 的是好友,就在表格(1,2)处打√;
这就是我们先前利用的传统办法,用邻接矩阵去解决。
某天,你把座位重新排了,比如座位 1 和座位 3 的同学换了位置,新的座位表,也就是新的邻接矩阵里,√的位置变了,但 “同学的好友关系没变”;
但如果有个 “死板的机器人”只看座位表,会误以为 “好友关系变了”—— 这就是传统模型的问题。
但传统的 “邻接矩阵” 表示法有个致命缺陷:
节点排序变了,邻接矩阵就变了,但图的本质没变。
图的 “连通性”(节点间的关系)是核心,
传统模型无法识别 “不同邻接矩阵对应同一个图”,会做出错误判断!
那么,邻接矩阵的致命缺陷到底是什么?
我们在前面已经提到过了,图分为两种,一种是有向图,一种是无向图。
那么现在请读者稍作思考,“朋友”该关系是有向图还是无向图?
无向图,对吧?
假设有 3 个节点 A、B、C,A 和 B 是好友,B 和 C 是好友 ,
按 “A→B→C” 的顺序,邻接矩阵的(1,2)和(2,3)是 1;
若按 “B→A→C” 的顺序,邻接矩阵的(1,2)和(1,3)是 1;
A-B-C 的链状结构;就是传统模型会把这两个 “不同的矩阵” 当成 “不同的数据”,输出不同的结果,但实际上这两个图的连通性完全一样,因为他们都是都
在规模上,图的节点排序有 “n! 种可能”
这还只是小规模数据,请你回忆一下我们在文章当中开头提到的《奥德赛》的例子,有非常多形形色色的人物,如果我们通过传统序列模型去构建图,一个图能对应 n! 个不同的邻接矩阵 ,传统模型需要学习 n! 种情况,根本学不过来,还容易过拟合。
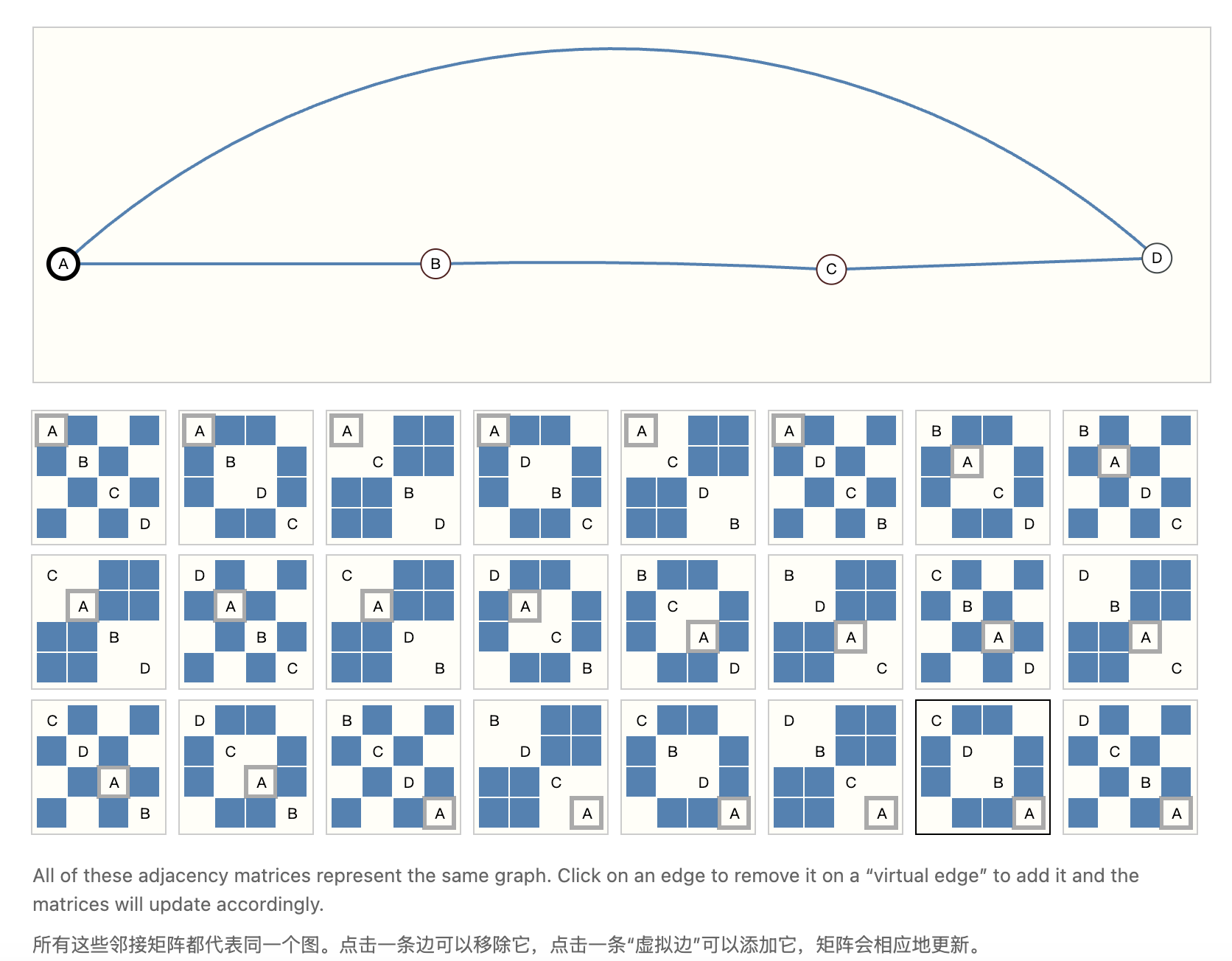
上面的例子展示了能够描述这个4节点小图的所有邻接矩阵。这已经是相当多的邻接矩阵了——对于像奥赛罗棋这样更大的例子,其数量更是难以处理。
3. 信息聚合复杂性
首先,大家必须知道什么是“信息聚合”。
信息聚合。就是每个节点要 “收集邻居节点的信息”,并把这些信息 “合并成新的信息”,用来更新自己的特征。这就
假设你想判断 “要不要去看某部电影”,你会问身边看过的朋友——
朋友 A 说 “剧情好”,朋友 B 说 “特效差”,朋友 C 说 “演员演技在线”。
你需要把这 3 个朋友的评价“聚合” 起来,比如 “优点:剧情 + 演技;缺点:特效”,再结合自己原本的偏好,也就是自身特征,最终决定 “去看” 还是 “不去看”。
这个例子当中,
你 --> 某个节点
你身边的朋友 --> 这个节点的邻居节点
朋友的评价 --> 邻居信息
结合自身的偏好 --> 自身特征
为什么信息聚合会如此复杂?
难点 1:邻居数量不固定,聚合函数要 “适配所有情况”
图像里每个像素的邻居数是固定的,但图中每个节点的邻居数可能天差地别:
社交网络里,普通用户可能只有 20 个朋友(20 个邻居),明星可能有 100 万粉丝(100 万个邻居);
分子图里,氢原子只有 1 个化学键(1 个邻居),碳原子可能有 4 个化学键(4 个邻居)。
这就给聚合函数出了难题:
同一个聚合函数,要能处理 “20 个输入” 和 “100 万个输入”,还得保证结果合理。
这种 “邻居数量可变” 带来的 “规模失衡” 和 “信息稀释”,就是第一个复杂性。
难点 2:邻居顺序不影响图结构,聚合函数必须 “排列不变”
之前我们提到过图的 “排列不变性”:把节点的编号打乱,图的实际关系没变,模型的聚合结果也应该不变。
但传统的聚合方式是 “顺序敏感” 的 ,若是邻居顺序变了,MLP 的输出会完全不同。这就要求 GNN 的聚合函数必须满足 “排列不变性”。
看似容易,但这会限制聚合函数的选择:
- 能满足的基础函数很少:只有 sum(求和)、mean(求平均)、max(求最大值)这几种;
- 这些基础函数又有缺陷:比如 max 会 “只看极端值”(假设邻居里有一个 “差评”,max 会忽略所有 “好评”),sum 和 mean 会 “模糊个体差异”(无法区分 “多个普通评价” 和 “一个关键评价”)。
要在 “排列不变” 和 “表达能力” 之间找平衡,是第二个复杂性。
难点 3:邻居信息有 “好有坏”,要能 “区分重要性”
现实中,邻居的信息不是都有用 —— 比如判断 “某篇论文是否重要”,这篇论文引用的 “顶会论文”和 “低质量会议论文”,权重应该不一样。
但基础聚合函数(sum/mean/max)都是 “平等对待所有邻居” 的:
- sum 会把顶会论文和低质量论文的信息同等相加;
- mean 会把两者的信息同等平均;
- max 可能只抓一个极端值,但没法针对性加权。
为了解决该问题,需要设计 “能给邻居分配权重” 的聚合函数(比如注意力机制),但这又会带来新的艰难:
- 怎么计算权重?得设计 “评分函数”(比如用节点特征的内积判断相似度);
- 怎么保证权重计算也满足 “排列不变性”?不能因为邻居顺序变了,权重就变了;
- 怎么避免过拟合?权重太多可能导致模型 “只关注少数邻居”,忽略全局信息。
这种 “需要区分邻居重要性,但又要兼顾排列不变性” 的矛盾,是第三个复杂性。
邻居节点就是难点 4:要融合 “多源信息”,不只
只看邻居节点。就是图里的信息不只有 “节点特征”,还有 “边特征” 和 “全局特征”—— 聚合时得把这些多源信息融合起来,而不
融合这些信息的难点在于:
- 不同信息的 “格式不一样”:节点特征是向量,边特征是另一个向量,全局特征是标量,没法直接相加;
- 不同信息的 “贡献不一样”:有的任务里边特征更重要,有的任务里全局特征更核心,需要动态调整权重;
- 融合后要保证 “排列不变性”:比如边特征的顺序变了,融合结果不能变。
这种 “多源信息格式不统一、贡献难量化” 的问题,是第四个复杂性。
六、图神经网络GNN的核心内容
1. GNN的回顾及核心特性
我们在上面谈到了challenge部分,接下来我们分几个层面分别来看我们要面临的挑战和应该怎么样解决。
根本矛盾;就是理解 “图的灵活 vs 模型的规整”
核心解决 “连接性表示” 和 “信息传递” 两大障碍;
学术层面(选择性看): 从 “邻接表→PNA” 解决排列不变性,从 “全局节点→JK-Net” 解决信息传递效率,从 “GraphSAINT→Cluster-GCN” 处理批处理问题 —— 每一个学术突破,都对应一个具体的技术挑战。
大家在前面提到了排座位表的例子,传统模型无法理解节点排序变了,邻接矩阵就变了,但图的本质没变
原文对与GNN下的定义
"A GNN is an optimizable transformation on all attributes of the graph (nodes, edges, global-context) that preserves graph symmetries (permutation invariances)."
GNN 是对图的所有属性(节点、边、全局)进行可优化的变换,且保持图的对称性(置换不变性)
原文当中有个很有意思也关键的点 :"graph-in,graph-out",
输入是图,输出也是图。

在什么情况下才能保证完成上面的挑战之一——置换不变性?
我们在上面提到了,启用集合论当中的对称函数
聚合函数:在消息传递时,用 sum/mean/max 合并邻居信息,确保邻居顺序不影响结果;
嵌入更新:用 MLP 将 “原节点嵌入” 和 “聚合后的邻居信息” 结合,生成新嵌入,MLP 的参数在所有节点上共享,避免对节点顺序的依赖。
2. GNN核心机制——消息传递
消息传递?就是什么
小朋友手拉手围成一圈,每次只能和左右的小朋友说话;
经过多次传递,每个玩家最终能知道 “离自己 3 步外的玩家” 的信息;
GNN 的 “消息传递” 就像这个过程 —— 节点通过邻居逐步获取远处的信息。
那么,每个小朋友获取信息分为几个步骤呢?
- 收集:目标节点获取所有邻居的嵌入;
- 聚合:用 sum/mean/max 合并邻居消息;
- 更新:用 MLP 结合 “原节点嵌入” 和 “聚合消息”,生成新嵌入。
那么某平台预测社交网络中用户的兴趣时,用户 A 的嵌入会聚合好友 B、C 的嵌入,用 sum 合并,再通过 MLP 更新,最终得到 A 的兴趣偏好。
消息传递的两种方向:
- 边→节点:边将信息传递给相连的节点;
- 节点→边:节点将信息传递给相连的边。
为了让全局属性也参与消息传递,论文引入主节点(master node)—— 一个虚拟节点,与所有节点和边相连,专门负责整合全局信息。
举个例子:在分子图中,主节点可以收集所有原子(节点)和共价键(边)的信息,从而生成整个分子的嵌入,用于预测毒性。
3. 的核心组件与演进
如何进阶设计的。就是这部分我们将按照阶段,由浅入深逐层学习GNN
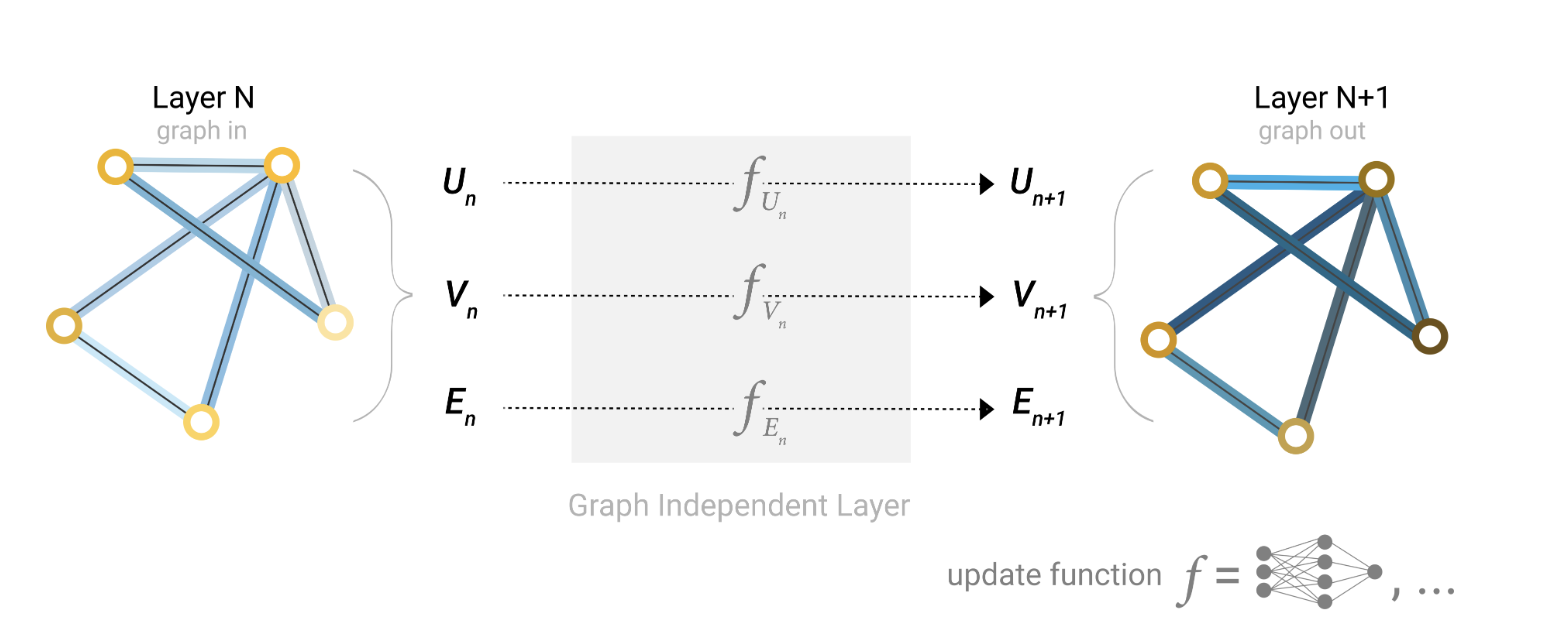
(1) 最简单的 GNN—— 独立更新属性(不利用连通性)
实现逻辑:用 3 个独立的多层感知器(MLP)分别处理节点、边、全局属性:
- 节点 MLP:输入节点原始属性(如分子中原子类型),输出更新后的节点嵌入;
- 边 MLP:输入边原始属性(如分子中共价键类型),输出更新后的边嵌入;
- 全局 MLP:输入全局原始属性(如分子分子量),输出更新后的全局嵌入。
关键特点:三个 MLP 完全独立,节点更新不依赖邻居,边更新不依赖节点,全局更新不依赖节点 / 边,
也就是说,三者互不依赖,仅做 “属性的独立特征变换”,未发挥图的结构优势。
可扩展性:可堆叠多层(如 2 层节点 MLP+2 层边 MLP),依据加深网络提升特征提取能力,但本质仍是“独立更新”。
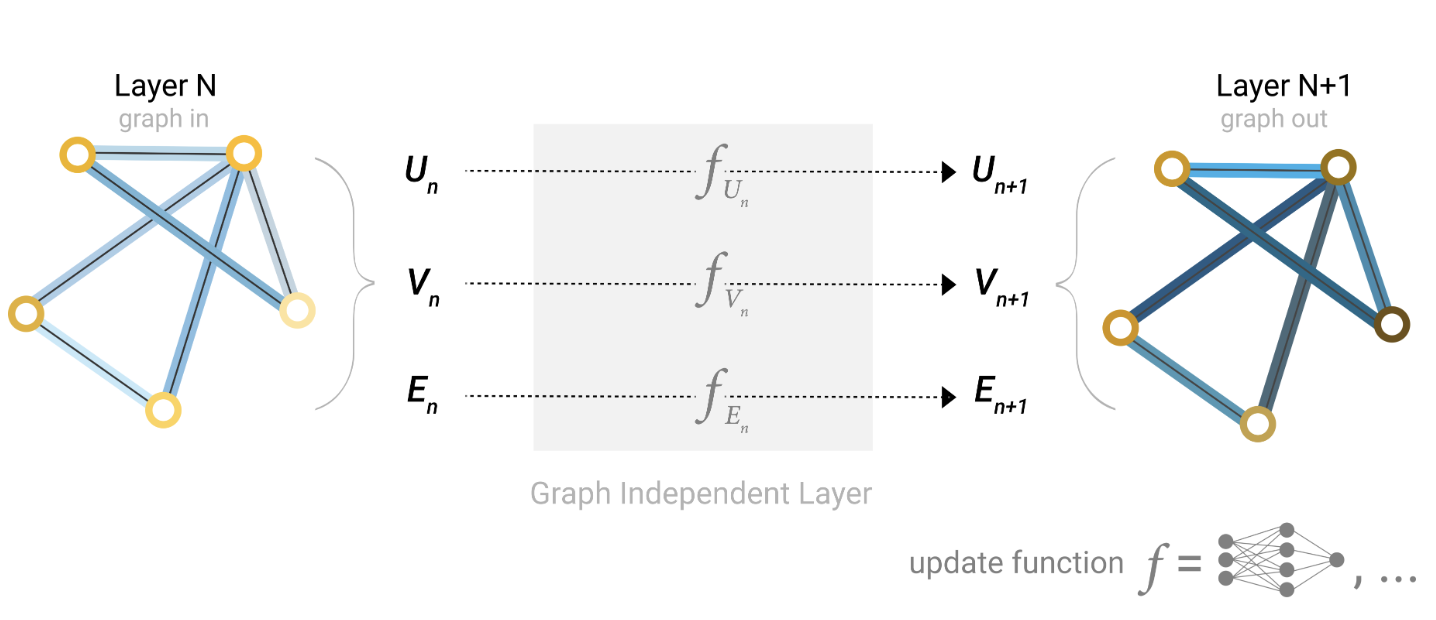
(2) 信息聚合(池化)—— 处理 “属性间信息传递” 疑问
我们在上一阶段已经看到了,要是使用三个MLP的话,没有利用到属性之间的关联,也就无法凸显“图的特征”
那么假设还是启用第一个例子的话,我们就无法判断该原文当中的“如果两个教练决裂了,各个学员倾向于效忠谁?”这个问题。
此时我们引入“信息聚合(池化)”,来解决这样的问题。
“将一类属性的嵌入,通过规则合并到另一类属性中” 的操作就是聚合
什么是池化?原文如下
1.For each item to be pooled,gathereach of their embeddings and concatenate them into a matrix.
2.The gathered embeddings are thenaggregated, usually via a sum operation.
这一步的学术关键仍然是置换不变性。也就是我们反复提到的(sum/mean/max)等函数
池化简单来说分为两步:
1.收集 : 找到目标属性对应的源属性嵌入,比如目标是节点,原属性就是它的相邻边。
2.聚合 : 使用置换不变操作合并源属性嵌入
比如说sum所有遍的嵌入,避免因为“邻居数量不同导致结果混乱”
三大应用场景
1. 边-->节点聚合 : 用自身边的信息更新节点
例如,社交网络中,节点通过收集相邻边的嵌入,sum聚合后更新自身嵌入——互动次数多的边,对用户嵌入的影响更大。
2. 节点-->全局聚合 : 用节点信息更新全局属性。
在分子图当中,全局属性手机所有节点的嵌入,mean聚合后更新。
3. 节点-->边聚合 : 用边两端的节点的信息去更新边。
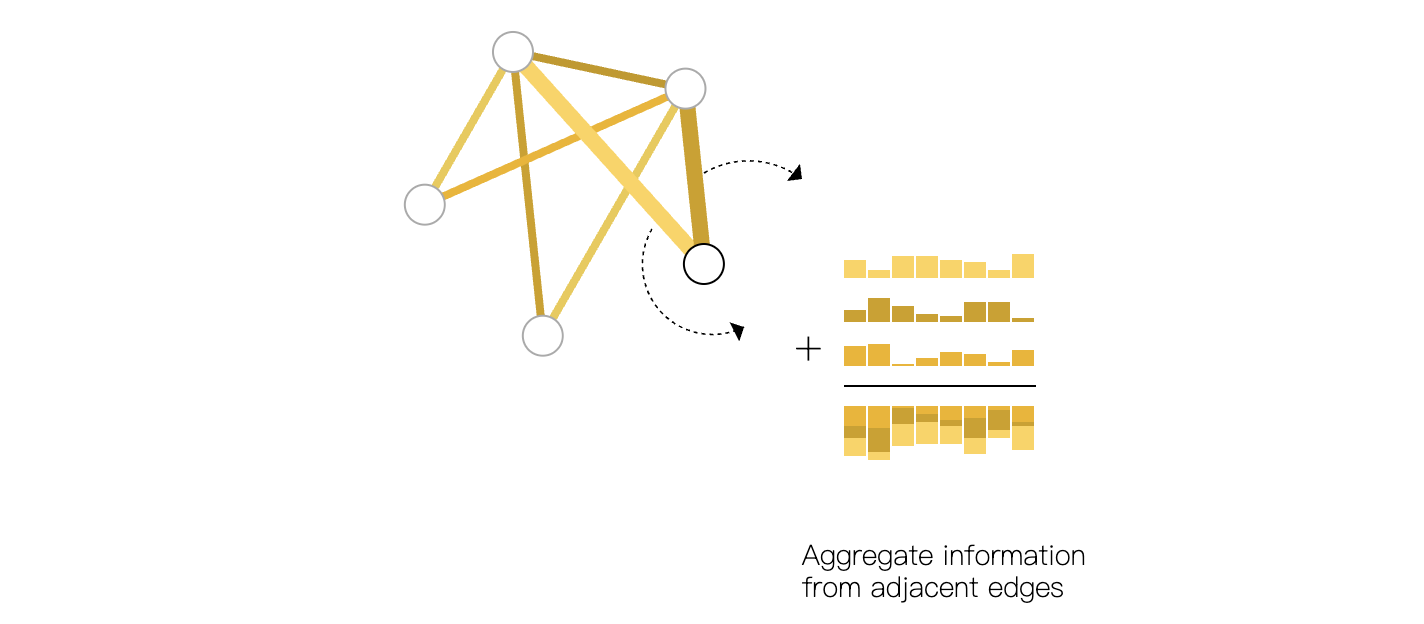
(3) 消息传递——利用图的联通性
核心疑问:信息聚合仅达成 “属性间传递”,未利用 “节点邻居的结构关系”(如 A 是 B 的邻居,B 是 C 的邻居,A 的信息需传递给 C),消息传递是 GNN 区别于传统模型的关键。
消息传递是 “节点通过相邻节点 / 边交换信息,更新自身嵌入” 的过程,原文以 “节点消息传递” 为例,
- 收集(Gather):目标节点 v,收集其所有直接邻居节点 u的嵌入(若有边属性,需同时收集边嵌入);
- 聚合(Aggregate):用 sum/mean/max合并所有邻居的嵌入,生成 “邻居聚合消息”;
- 更新(Update):通过 MLP 将 “目标节点 v 的原嵌入” 与 “邻居聚合消息” 结合,生成 v 的新嵌入 —— 新嵌入既包含 v 自身信息,也包含邻居的结构信息。
原文用图像卷积辅助理解:
消息传递类似图像中的 CNN 卷积:CNN 中每个像素聚合 “3×3 邻域像素” 的信息,GNN 中每个节点聚合 “所有邻居节点” 的信息;
差异:CNN 的邻域大小固定(如 3×3),GNN 的邻居数量可变,如 A 有 5 个邻居,B 有 10 个邻居,因此必须用 sum/mean/max 替代固定窗口卷积。
层数的意义(原文重点强调):
堆叠 k 层消息传递,节点 v 的嵌入可包括 “k 步外的邻居信息”(1 层:直接邻居;2 层:直接邻居的邻居;以此类推);
例:分子图中,2 层消息传递后,原子 A 的嵌入可包含 “与 A 直接相连的原子 B,以及 B 相连的原子 C” 的信息,覆盖分子的局部官能团结构。
(4) 边表示与全局表示学习
Learning edge representations 学习边表示
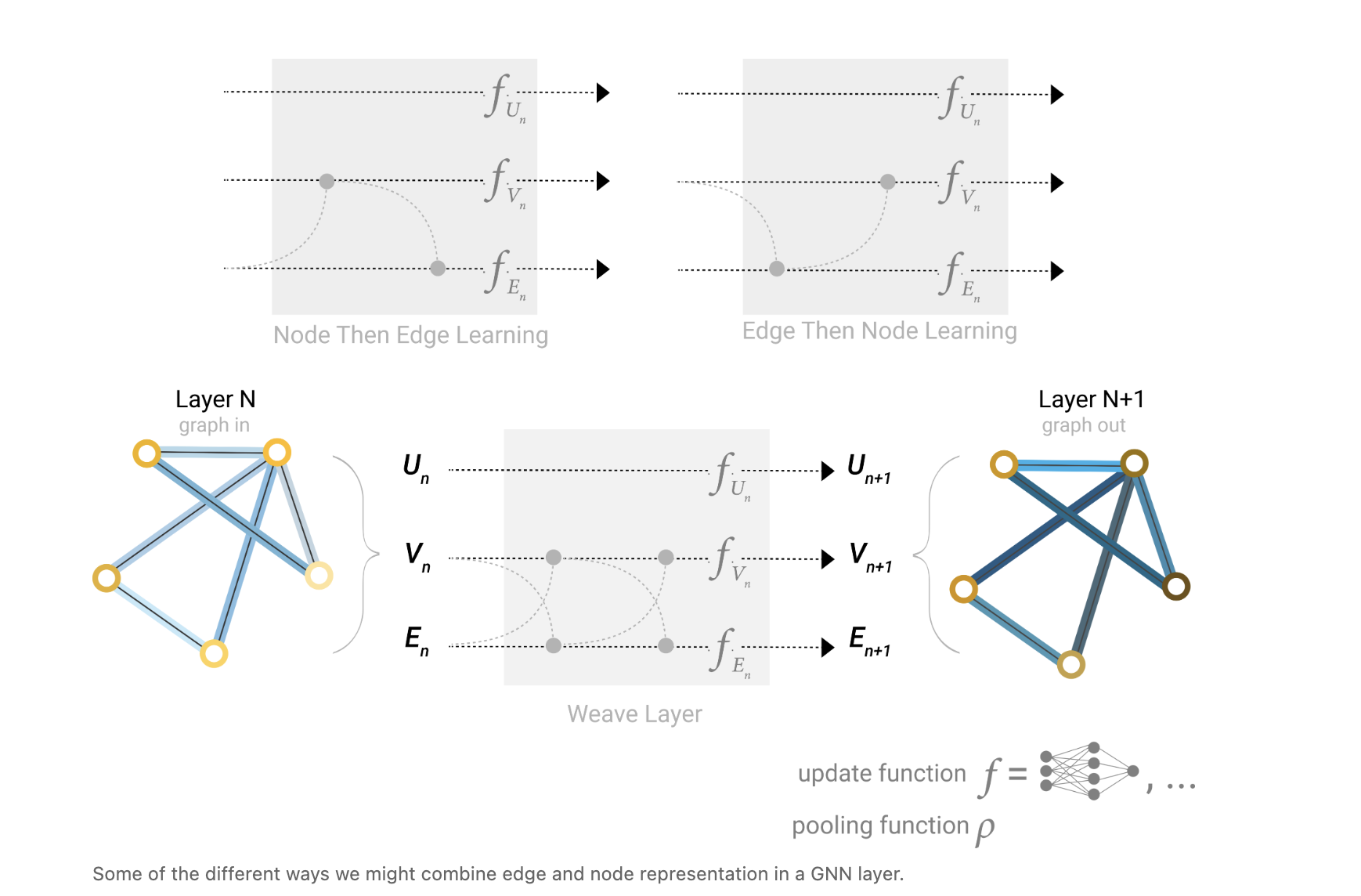
这里提出了一个新的场景:若资料集仅含节点信息(无边属性),或需用节点信息增强边特征,
原文提出两种途径:
线性映射:将节点嵌入依据线性层转换到 “边特征空间”,生成边的初始嵌入;
拼接更新:将边两端节点的嵌入拼接,输入 MLP 生成边的新嵌入 —— 让边嵌入包含节点的上下文信息。
Adding global representations 添加全局表征
翻译如下:
图中彼此距离较远的节点可能永远无法高效地向对方传递信息,即便大家多次应用消息传递也是如此。
对于一个节点而言,假如我们有k层,信息最多只能传播k步远。
这在预测任务依赖于距离较远的节点或节点组的情况下可能会成为困难。
一种解决方案是让所有节点都能够相互传递信息。但对于大型图来说,这很快会导致计算成本过高(不过这种被称为“虚拟边”的技巧已被用于分子等小型图)。
怎么应对呢?
Adding global representations 添加全局表征!
新增一个 “虚拟主节点”,与图中所有节点、所有边直接连通。
主节点参与消息传递:收集所有节点和边的嵌入,更新自身嵌入;同时,主节点的嵌入也传递给所有节点和边。
这样就能让主节点成为 “全局信息桥梁”,长距离节点可通过主节点间接传递信息,避免多层堆叠导致的信息丢失。
4. 总结
GNN 的设计围绕 “如何在保持置换不变性的前提下,利用图的连通性与属性信息” 展开。
先通过 “独立更新” 建立基础框架,再通过 “信息聚合” 达成属性间传递,最后通过 “消息传递” 利用连通性;
用 “主节点” 解决长距离传递问题,用 “线性映射/拼接” 补充边表示;
七、GNN Playground(GNN关键设计选择)
这里作者在原文中给出的的具体实验暂且不提,大家只关注GNN的关键设计选择
1. 聚合函数的选择
在作者的实验当中,三种函数的性能差异较小,但sum的效果略高于mean和max。
那么这三种函数应当如何选择呢?
- sum:适合需保留 “邻居数量信息” 的场景,比如说在某个分子当中,原子的总数可能对分子的化学性质有影响,这样可以平衡局部分布与异常值;
- mean:适合 “邻居数量差异大” 的场景,比如说我有5个朋友,但是迪丽热巴有1000个朋友,这样可以经过归一化避免度数大的节点主导聚合结果;
- max:适合需 “突出显著特征” 的场景,比如在有机化学当中,我们一定会分辨“三键”、“双键”和“单键”,这样可以捕捉邻居中的关键信息。
结论:
无绝对最优,但是sum的鲁棒性最强。
2. 层数的选择
在 “分子气味预测”“空手道俱乐部分类” 等任务中,2 层 GNN 的准确率显著高于 3 层、4 层;
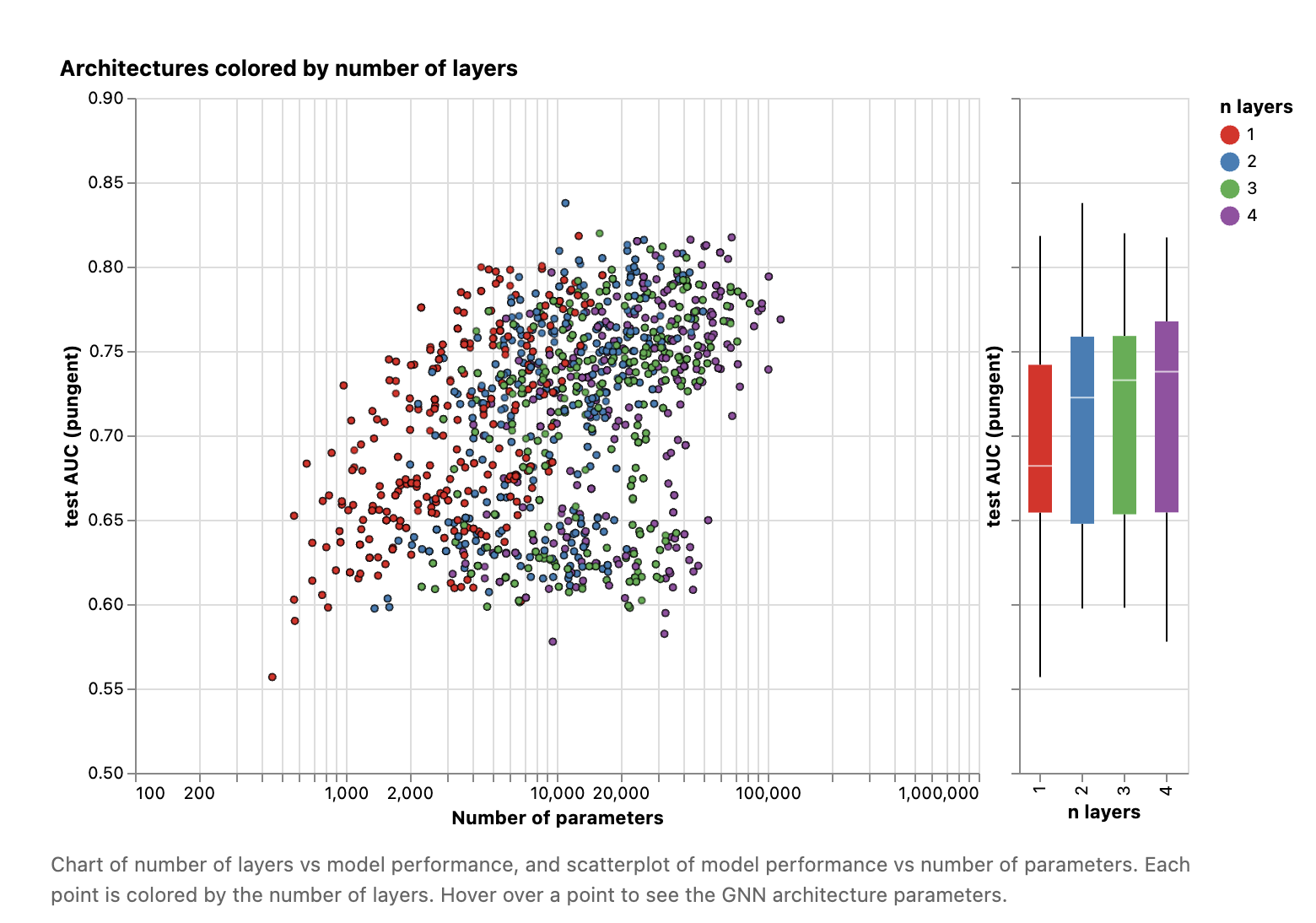
原文解释:层数过多会导致 “节点嵌入稀释”—— 所有节点的嵌入逐渐趋同,如 A 和 D 的嵌入差异变小,无法区分结构相似但属性不同的节点 / 图;
结论:
入门任务优先用 2 层,复杂图可以尝试 3 层,但需借助验证集监控 “嵌入稀释”。
3. 属性通信的选择
属性通信指 “节点、边、全局属性间的消息传递方向”(如节点→边、边→节点、全局→节点等);
原文通过对比 “仅节点间通信”、“节点 + 边双向通信”和“节点 + 边 + 全局三向通信” 三种方案,结果显示:通信方向越多,模型性能越好;
结论:
采用 Graph Nets 架构的 “全属性通信”,
同时开启节点→边、边→节点、节点→全局、全局→节点、边→全局、全局→边的通信,让所有属性相互辅助,最大化利用图的结构与属性信息。
-----------------------------------------------------------------------------------------------
至此,文章结束!
写到这里,关于GNN原论文的核心思想与架构已主要剖析完毕。然而,真正的精髓往往藏在细节之中,比如消息传递的具体达成、各类聚合函数的优劣对比,以及在真实数据集上的性能狂飙。这些内容足以自成一体,我将它们规划为 《GNN原论文精读》系列的下一个篇章,届时我们会一起深入科技腹地,拆解每一个齿轮。
创作这样一篇长文,犹如一次深入的技术探险,期间反复揣摩论文本意,并思考如何呈现给各位,过程虽烧脑却也无比酣畅。技术写作于我,是一个“把书读薄,再把书读厚”的过程,任何关于本文的讨论、指正或更优见解,都欢迎在评论区与我碰撞——最好的理解,永远诞生于思维的交流之中。
最后,恰逢1024程序员节刚过,愿你我永远保持此种 Hack the World 的极客精神,在0与1的世界里,建造属于我们的罗马。
祝你一生幸福!




 浙公网安备 33010602011771号
浙公网安备 33010602011771号