运动控制教学——5分钟学会Dijkstra与A*搜索算法！（附仿真视频及代码） - 教程

路径规划算法详解：从Dijkstra到A*的完整攻略

从GPS导航到机器人路径规划，这些算法每天都在默默改变着我们的生活。今天我们就来彻底搞懂两个最重要的路径搜索算法！

为什么要学习路径搜索算法？

想象一下，你正在开发一个扫地机器人，它需要在房间里找到从A点到B点的最短路径，同时避开障碍物。或者你在设计一个无人机配送系统，需要在复杂的城市环境中规划最优飞行路线。这些场景的核心都离不开一个问题：如何在图中找到两点之间的最优路径？

今天我们要深入学习的两个算法——Dijkstra和A*，正是解决这类问题的经典方案。

两大算法对比一览

特性	Dijkstra算法	A*算法
核心思想	广度优先，保证最优解	启发式搜索，有方向性
时间复杂度	O((V+E)logV)	O(b^d)
空间复杂度	O(V)	O(b^d)
是否保证最优	是	是（启发函数满足条件时）
搜索效率	较慢，全方位搜索	较快，有目标导向
适用场景	单源最短路径	点对点路径搜索

Dijkstra算法：稳扎稳打的经典之选

算法原理深度剖析

Dijkstra算法由荷兰计算机科学家Edsger Dijkstra在1956年提出，它的核心思想可以用一个生活化的比喻来理解：

想象你站在一个十字路口中心，手里拿着一把石子。你要找到到达所有地方的最短路径，于是你开始向四面八方抛石子。每次你都选择离你最近的那个还没到达的地点，然后从那里继续抛石子。

这个过程用数学语言描述就是：

1. 初始化：设起点距离为0，其他所有点距离为无穷大
2. 贪心选择：每次选择当前距离最小且未访问的节点
3. 松弛操作：更新该节点所有邻居的距离
4. 重复：直到所有节点都被访问

核心代码实现

import heapq
from collections import defaultdict
def dijkstra(graph, start):
# 初始化距离字典，所有点距离为无穷大
distances = defaultdict(lambda: float('inf'))
distances[start] = 0
# 优先队列，存储(距离, 节点)
pq = [(0, start)]
visited = set()
while pq:
current_dist, current = heapq.heappop(pq)
# 如果已访问过，跳过
if current in visited:
continue
visited.add(current)
# 松弛操作：更新邻居节点距离
for neighbor, weight in graph[current].items():
distance = current_dist + weight
# 如果找到更短路径，更新距离
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(pq, (distance, neighbor))
return distances
# 使用示例
graph = {
'A': {'B': 4, 'C': 2},
'B': {'C': 1, 'D': 5},
'C': {'D': 8, 'E': 10},
'D': {'E': 2},
'E': {}
}
result = dijkstra(graph, 'A')
print(f"从A点到各点的最短距离：{dict(result)}")

仿真演示视频(源码私信)

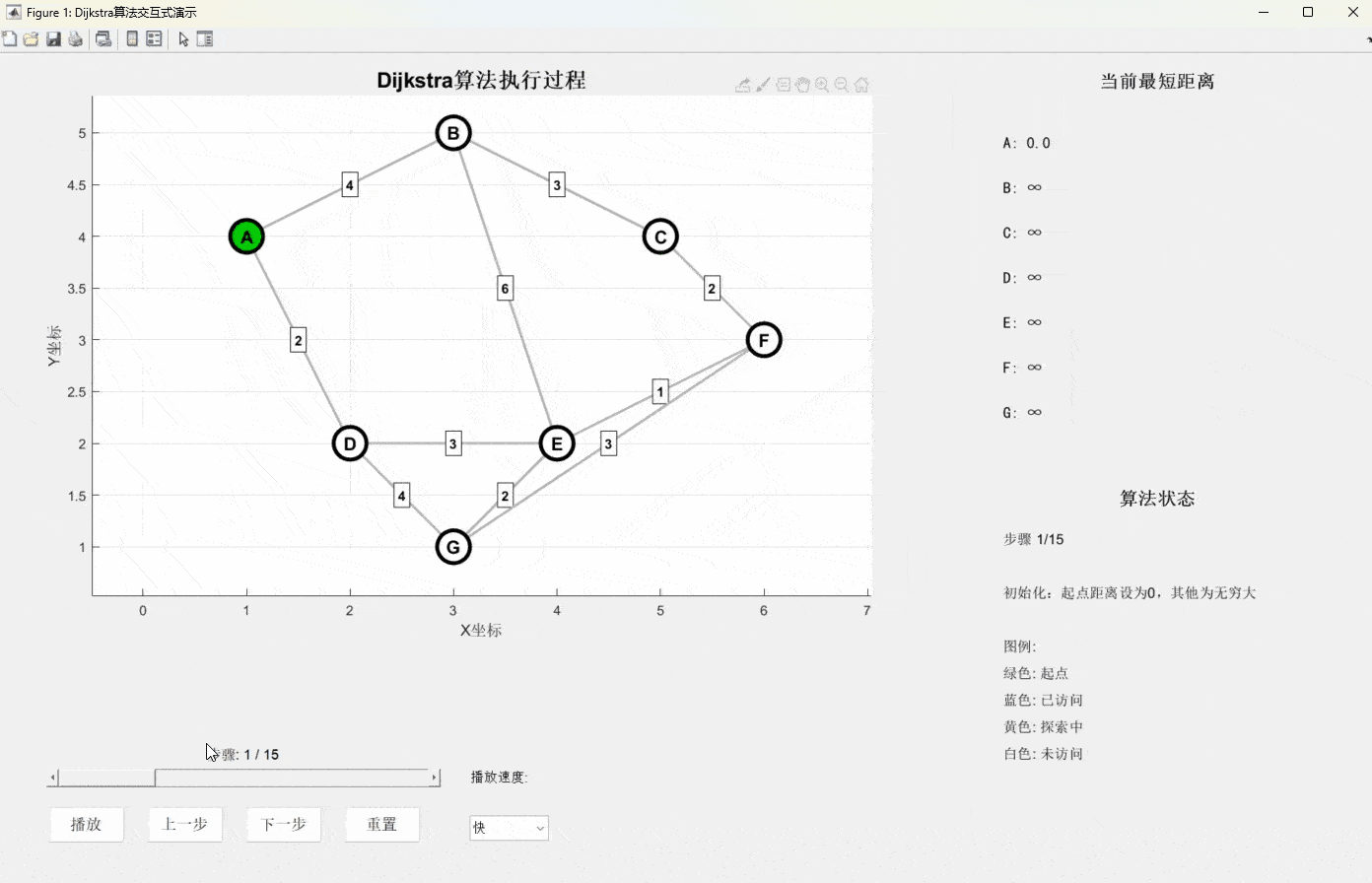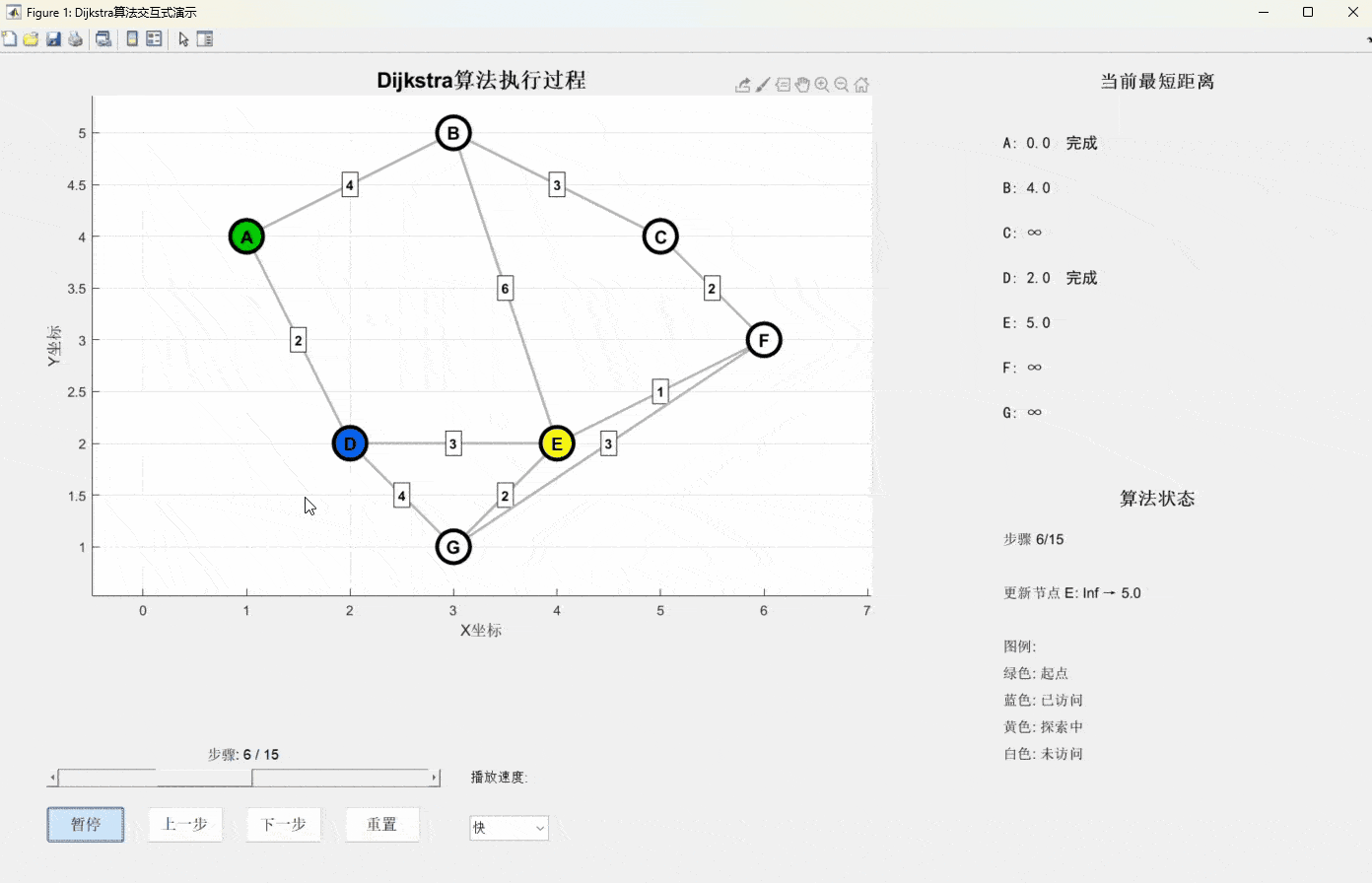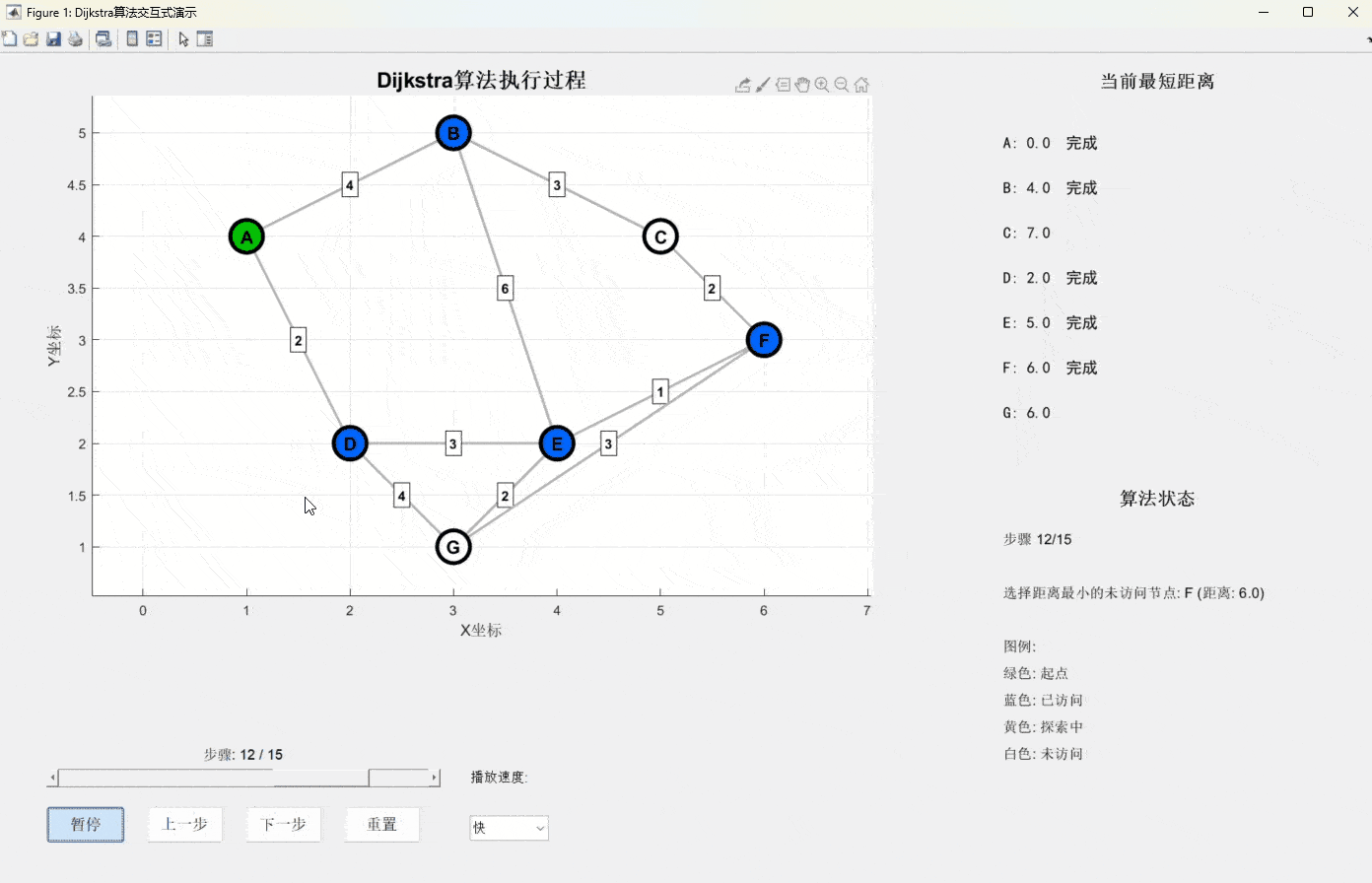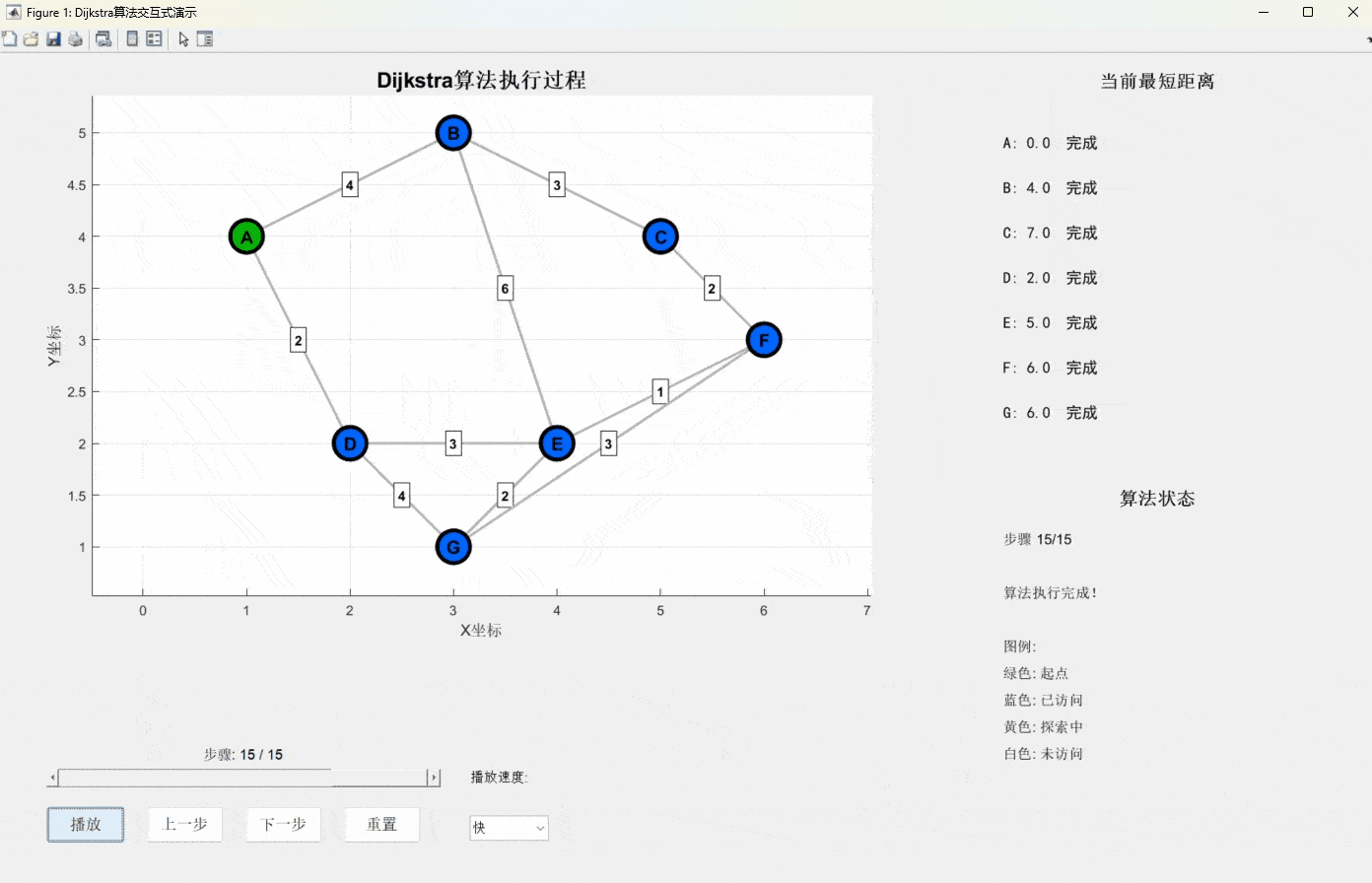
算法特点分析

优势：

• ✅ 保证最优解：只要边权重非负，必然找到最短路径
• ✅ 适用性广：可以一次性求出起点到所有其他点的最短距离
• ✅ 稳定性强：不受启发函数影响，结果可预测

劣势：

• ❌ 效率相对较低：需要遍历所有可能的节点
• ❌ 内存消耗大：需要存储到所有节点的距离信息

A*算法：智能高效的明星算法

算法原理深度剖析

A算法是对Dijkstra算法的智能升级，它引入了启发式函数的概念。如果说Dijkstra是"盲目"搜索，那么A就是"带着目标"搜索。

A*算法的核心公式：f(n) = g(n) + h(n)

• g(n)：从起点到节点n的实际距离（已知）
• h(n)：从节点n到终点的预估距离（启发函数）
• f(n)：预估的从起点经过n到终点的总距离

启发函数的选择艺术

常用的启发函数包括：

1. 曼哈顿距离（适用于网格图）：|x1-x2| + |y1-y2|
2. 欧几里得距离（适用于连续空间）：sqrt((x1-x2)² + (y1-y2)²)
3. 切比雪夫距离（允许对角移动）：max(|x1-x2|, |y1-y2|)

核心代码实现

import heapq
import math
def a_star(graph, start, goal, heuristic):
# 初始化
open_set = [(0, start)]  # (f_score, node)
came_from = {}
g_score = {start: 0}
f_score = {start: heuristic(start, goal)}
while open_set:
current_f, current = heapq.heappop(open_set)
# 找到目标
if current == goal:
path = []
while current in came_from:
path.append(current)
current = came_from[current]
path.append(start)
return path[::-1]
# 探索邻居节点
for neighbor, weight in graph[current].items():
tentative_g = g_score[current] + weight
if neighbor not in g_score or tentative_g < g_score[neighbor]:
came_from[neighbor] = current
g_score[neighbor] = tentative_g
f_score[neighbor] = tentative_g + heuristic(neighbor, goal)
heapq.heappush(open_set, (f_score[neighbor], neighbor))
return []  # 未找到路径
# 二维网格的曼哈顿距离启发函数
def manhattan_distance(node1, node2):
return abs(node1[0] - node2[0]) + abs(node1[1] - node2[1])
# 使用示例（二维网格）
grid_graph = {
(0,0): {(0,1): 1, (1,0): 1},
(0,1): {(0,0): 1, (0,2): 1, (1,1): 1},
(0,2): {(0,1): 1, (1,2): 1},
(1,0): {(0,0): 1, (1,1): 1, (2,0): 1},
(1,1): {(0,1): 1, (1,0): 1, (1,2): 1, (2,1): 1},
(1,2): {(0,2): 1, (1,1): 1, (2,2): 1},
(2,0): {(1,0): 1, (2,1): 1},
(2,1): {(2,0): 1, (1,1): 1, (2,2): 1},
(2,2): {(1,2): 1, (2,1): 1}
}
path = a_star(grid_graph, (0,0), (2,2), manhattan_distance)
print(f"最优路径：{path}")

仿真演示视频(源码私信)

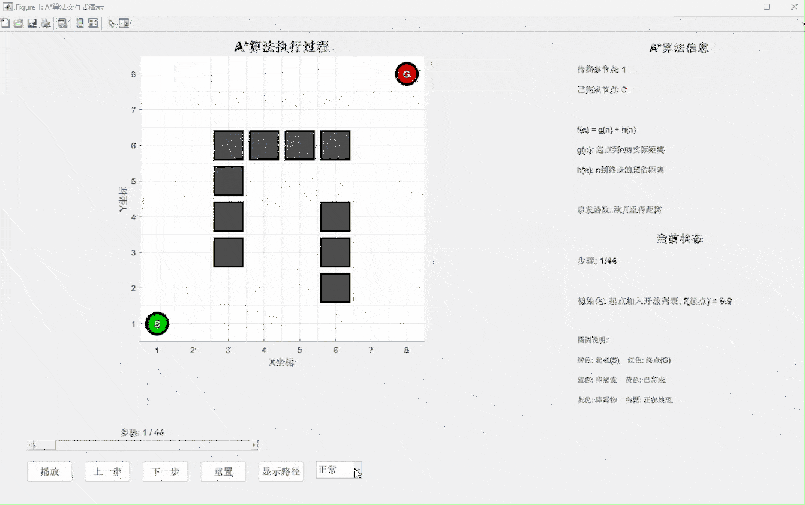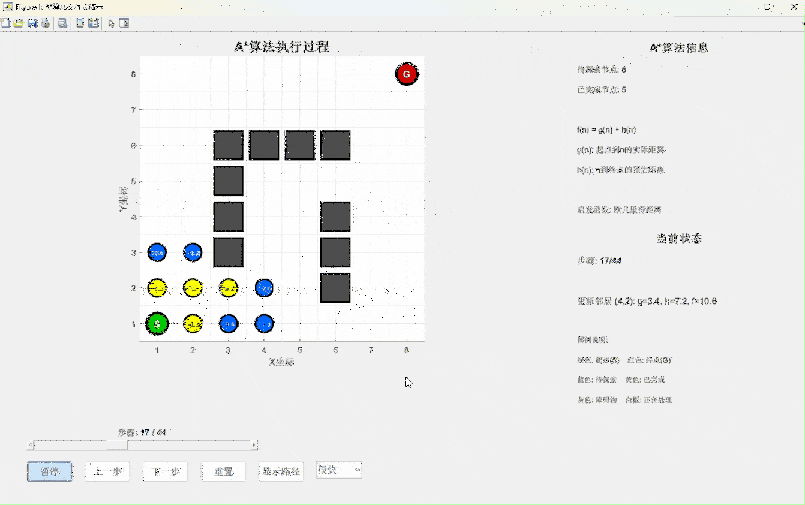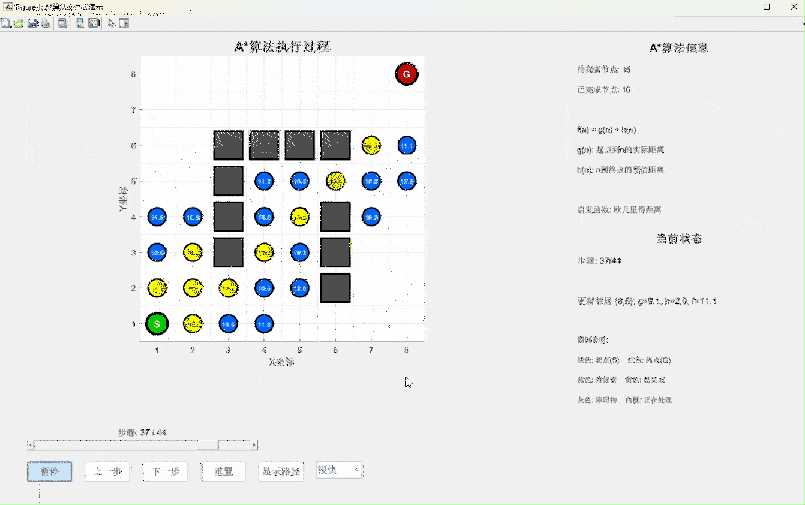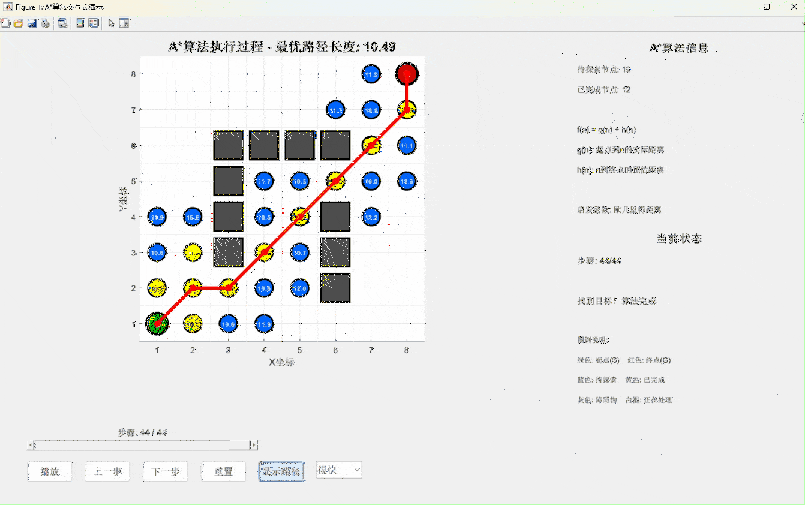
算法特点分析

优势：

• ✅ 效率高：有目标导向，搜索节点数量少
• ✅ 保证最优：启发函数满足可采纳性时保证最优解
• ✅ 灵活性强：可以根据具体场景调整启发函数

劣势：

• ❌ 内存需求大：需要存储open_set和closed_set
• ❌ 启发函数依赖：启发函数选择不当会影响性能

️ 前沿应用领域详解

1. 智能机器人导航

应用场景：

• 服务机器人：在酒店、医院等环境中自主导航
• 扫地机器人：规划清扫路径，避开障碍物
• 工业AGV：在工厂内运输货物的最优路径规划

技术要点：

• 使用激光雷达构建环境地图
• 结合动态障碍物检测
• 实时路径重规划能力

2. 机械臂路径规划

应用场景：

• 装配线机器人：在3D空间中规划关节运动轨迹
• 手术机器人：精确的路径控制，避开重要器官
• 焊接机器人：优化焊接路径，提高效率

技术要点：

• 高维配置空间的路径搜索
• 关节角度约束处理
• 碰撞检测与避免

3. 无人机航线规划

应用场景：

• 物流配送：城市环境下的最优配送路线
• 农业植保：农田作业路径优化
• 救援搜索：灾区搜救的航线规划

技术要点：

• 3D空间路径规划
• 气象条件影响考虑
• 禁飞区域规避

实战踩坑经验分享

常见问题1：启发函数选择不当

问题描述：
初学者经常选择不合适的启发函数，导致A*算法性能下降甚至失去最优性。

解决方案：

# ❌ 错误：过度估计的启发函数
def bad_heuristic(node, goal):
return manhattan_distance(node, goal) * 2  # 过度估计
# ✅ 正确：可采纳的启发函数
def good_heuristic(node, goal):
return manhattan_distance(node, goal)  # 永远不会过度估计

核心要点：

• 启发函数必须是可采纳的（永远不会过度估计）
• 启发函数越接近真实距离，A*效率越高
• 当启发函数为0时，A*退化为Dijkstra算法

常见问题2：优先队列重复元素处理

问题描述：
在实现过程中，同一个节点可能会被多次加入优先队列，导致重复处理。

解决方案：

# ✅ 改进版本：避免重复处理
def improved_a_star(graph, start, goal, heuristic):
open_set = [(0, start)]
closed_set = set()  # 已处理的节点
came_from = {}
g_score = {start: 0}
while open_set:
current_f, current = heapq.heappop(open_set)
# 关键：检查是否已处理过
if current in closed_set:
continue
closed_set.add(current)
if current == goal:
# 重建路径
path = []
while current in came_from:
path.append(current)
current = came_from[current]
path.append(start)
return path[::-1]
# 继续处理邻居...

常见问题3：大规模图的内存优化

问题描述：
处理大规模路径规划时，内存消耗过大导致程序崩溃。

解决方案：

1. 使用生成器：动态生成邻居节点，不预先存储整个图
2. 分层搜索：先粗粒度搜索，再精细化
3. 内存池管理：重复利用已分配的内存空间

常见问题4：动态环境适应

问题描述：
静态算法无法处理实时变化的环境（如移动障碍物）。

解决方案：

class DynamicAStar:
def __init__(self, graph, heuristic):
self.graph = graph
self.heuristic = heuristic
self.cache = {}  # 缓存部分计算结果
def replan(self, start, goal, changed_edges):
# 只重新计算受影响的部分
if self.is_cache_valid(changed_edges):
return self.incremental_search(start, goal)
else:
self.cache.clear()
return self.full_search(start, goal)

性能优化技巧

1. 双向搜索

def bidirectional_a_star(graph, start, goal, heuristic):
# 从起点和终点同时开始搜索
# 当两个搜索波前相遇时停止
pass  # 实现细节较复杂，但能显著提升大图性能

2. 分层图结构
对于大规模地图，可以构建分层图：

• 粗层：用于长距离规划
• 细层：用于局部精确导航

3. 并行化处理
利用多核CPU并行探索不同方向的路径。

算法性能对比实测

基于1000x1000网格地图的测试结果：

算法	平均搜索节点数	执行时间(ms)	内存占用(MB)
Dijkstra	125,000	850	45
A(曼哈顿)*	8,500	95	32
A(欧几里得)*	7,200	88	30

结论： A*算法在搜索效率上比Dijkstra提升了约10倍，内存使用也更加高效。

总结

通过今天的深入学习，我们掌握了两个核心路径搜索算法：

Dijkstra算法适合需要计算单源到所有点最短路径的场景，算法稳定可靠，是许多其他算法的基础。

A*算法在点对点路径搜索中表现卓越，通过引入启发函数实现了效率与准确性的完美平衡，是现代路径规划的首选算法。

在机器人导航、机械臂控制、无人机航线规划等前沿技术领域，这些算法正在发挥着越来越重要的作用。掌握它们的原理和实现，将为你在人工智能和机器人技术领域的发展奠定坚实基础。

记住，算法的选择没有绝对的好坏，只有是否适合具体的应用场景。在实际项目中，要根据数据规模、实时性要求、精度需求等因素来选择最合适的算法。