深入解析:考研复习-线性代数-第二章-矩阵
方阵的幂运算

1.方阵的幂运算
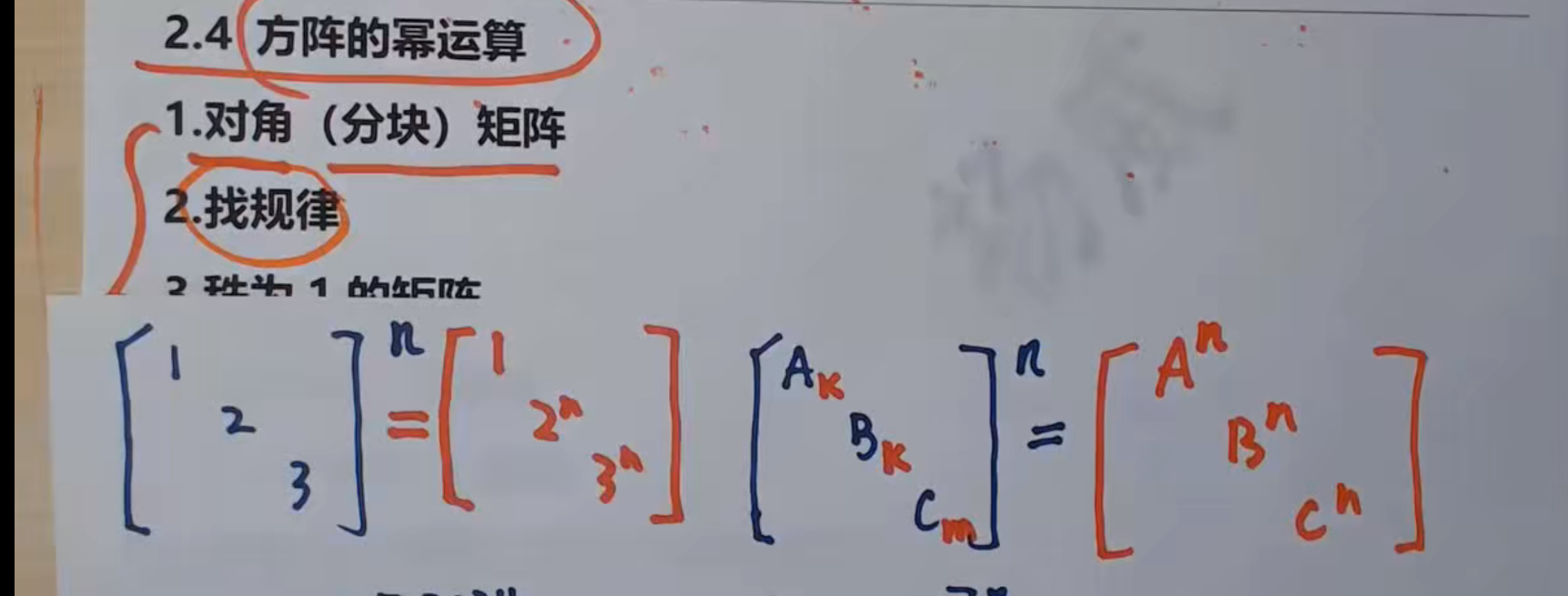
2.找规律
即直接手算多次即可发现规律
3.秩1矩阵的高次幂计算
其本质写成一行×一列
高次幂的推到如下

4.A可拆成E+B,B的多次幂为0,用多项式定理可求高次幂
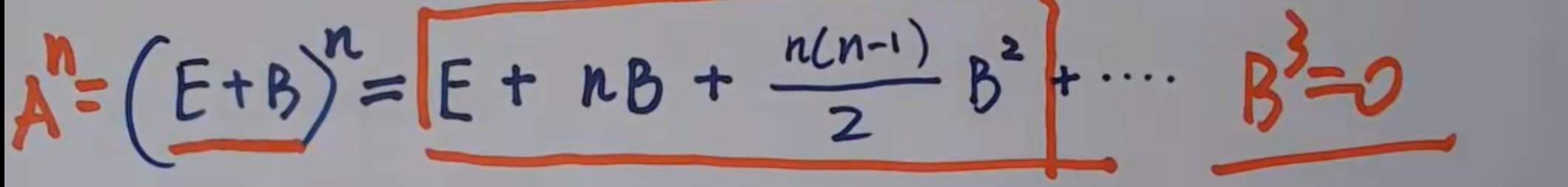
5.矩阵相似
证明
A*A=p-1Bp*p-1Bp=PB²P

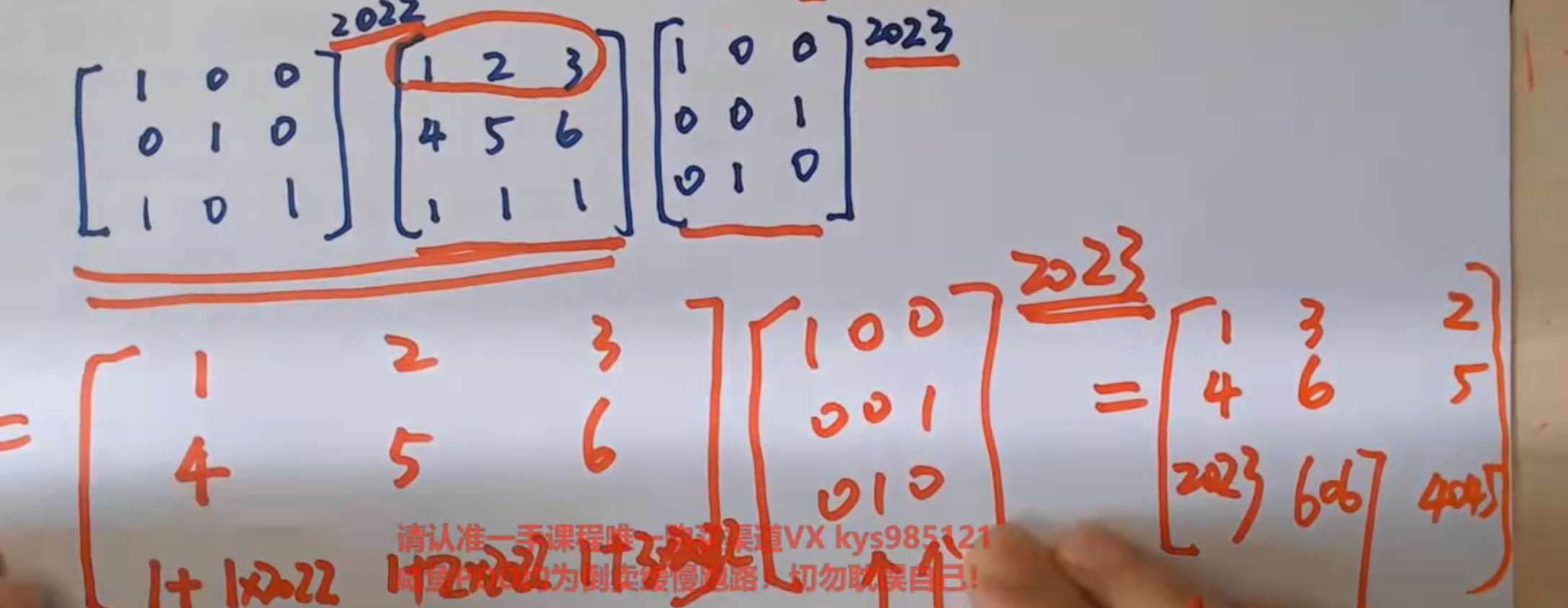
6.初等变换
每一个初等变换的n次方都是对该初等变换进行n次
方阵乘积的行列式
即两个n阶方阵相乘,其互换位置后的行列式也相同且可拆分
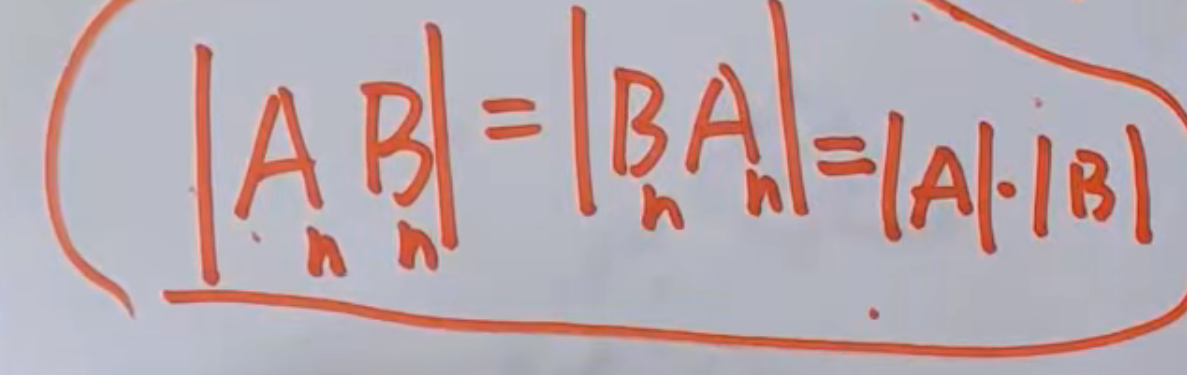
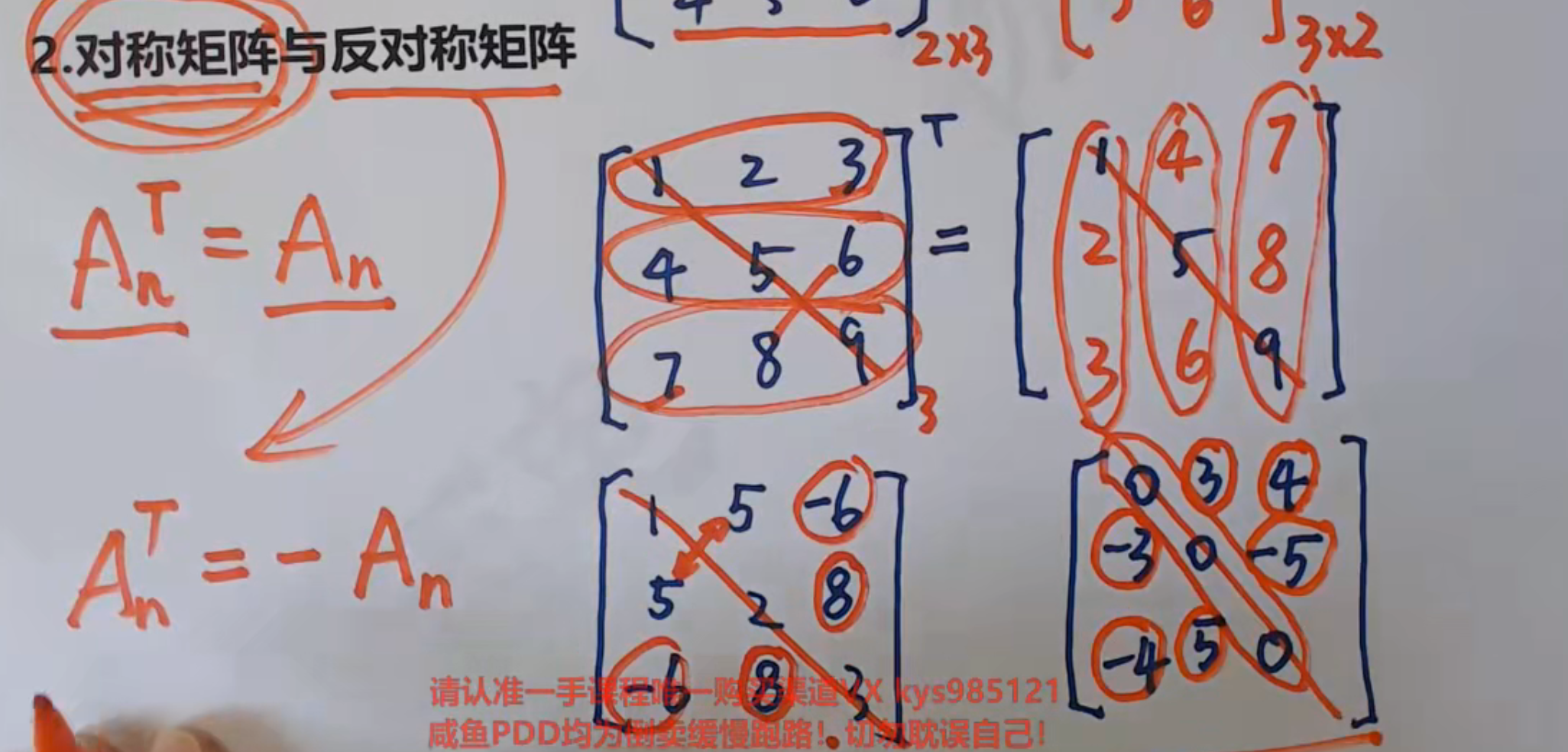
对称矩阵的概念
二阶方阵的伴随

矩阵可逆的充分必要条件

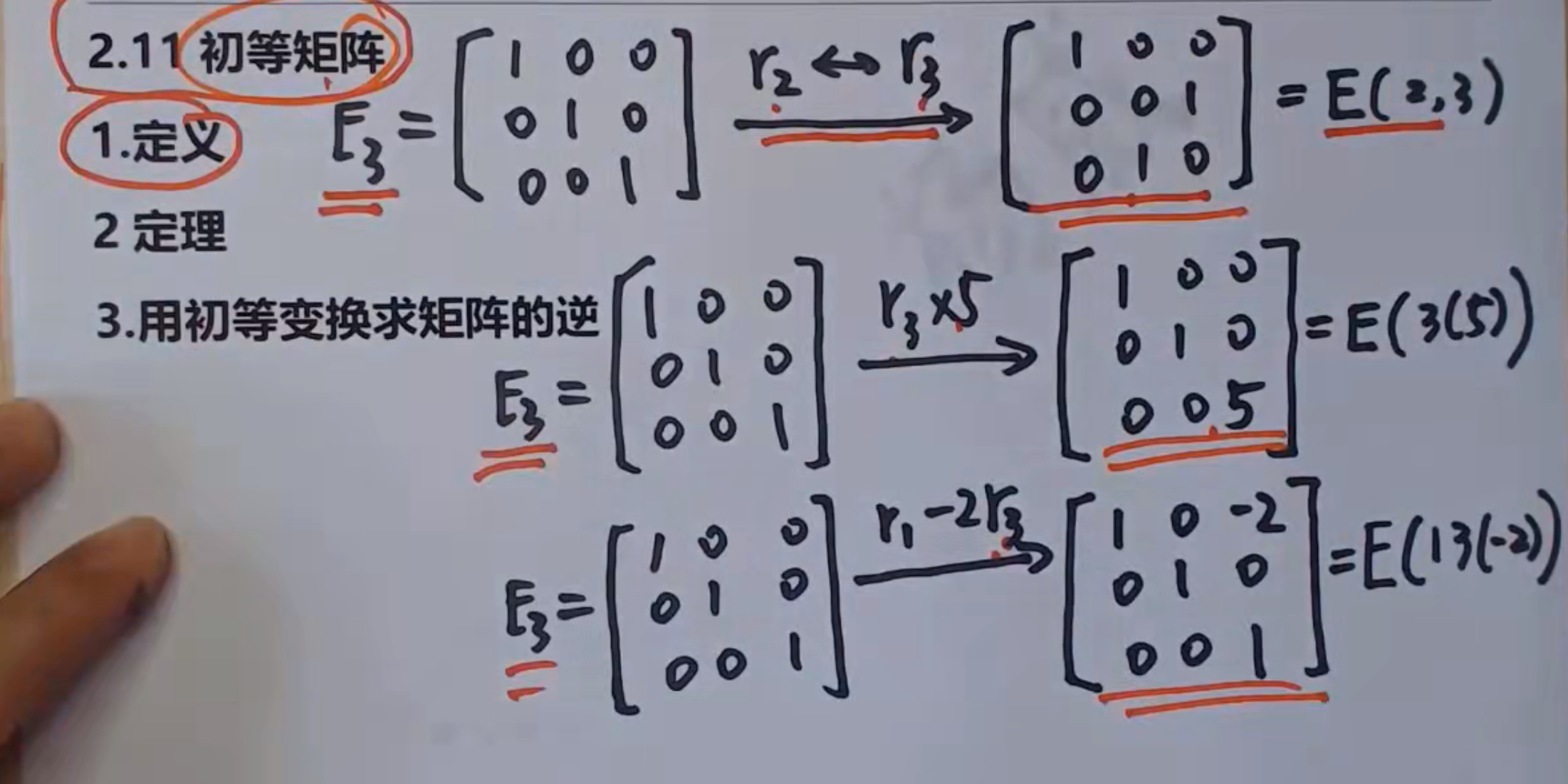
初等矩阵
单位阵经历过一次初等变换得到的矩阵成为初等矩阵
初等行变换求A的逆
如下所示已知AB 求A-1B

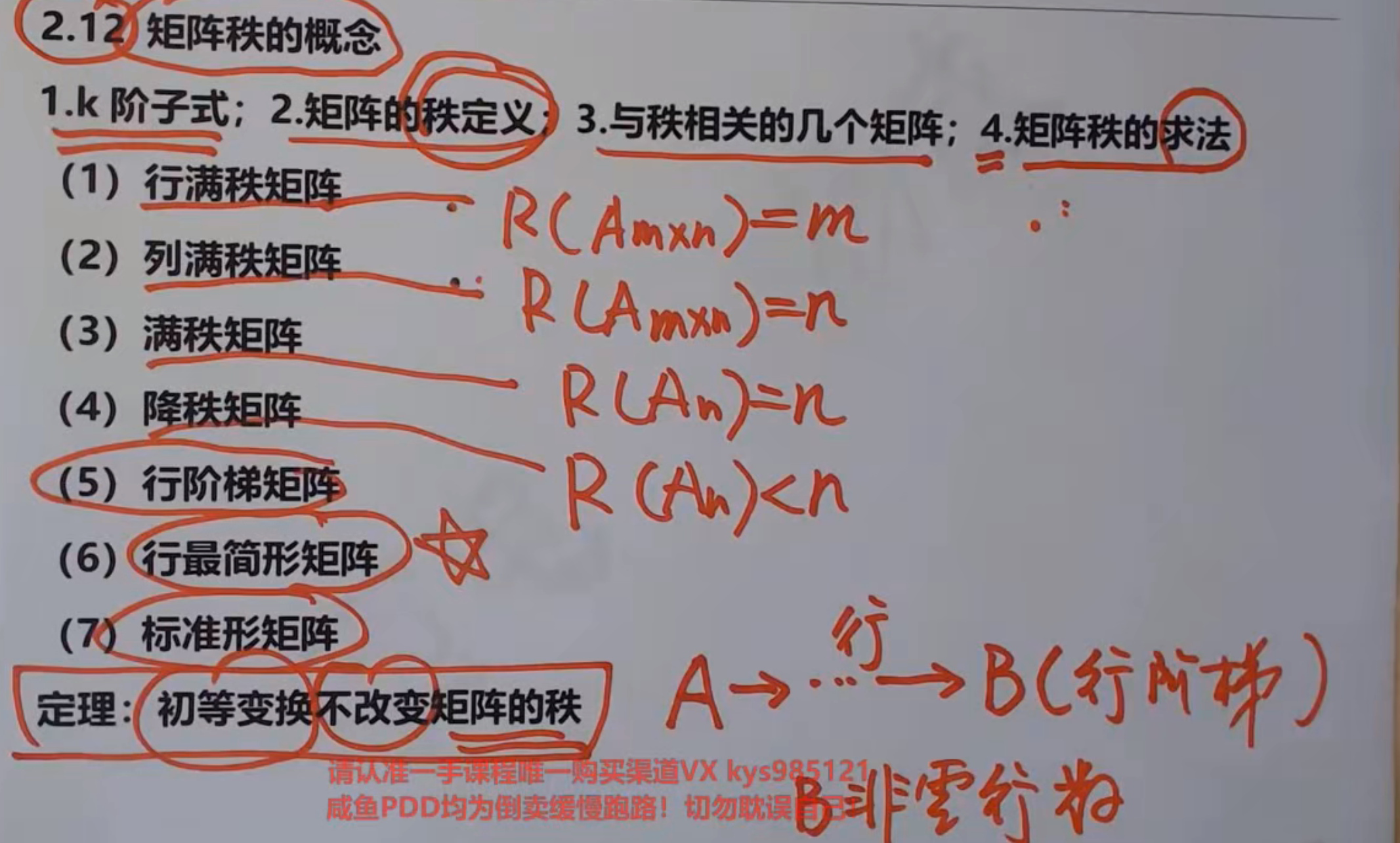
矩阵的秩的概念
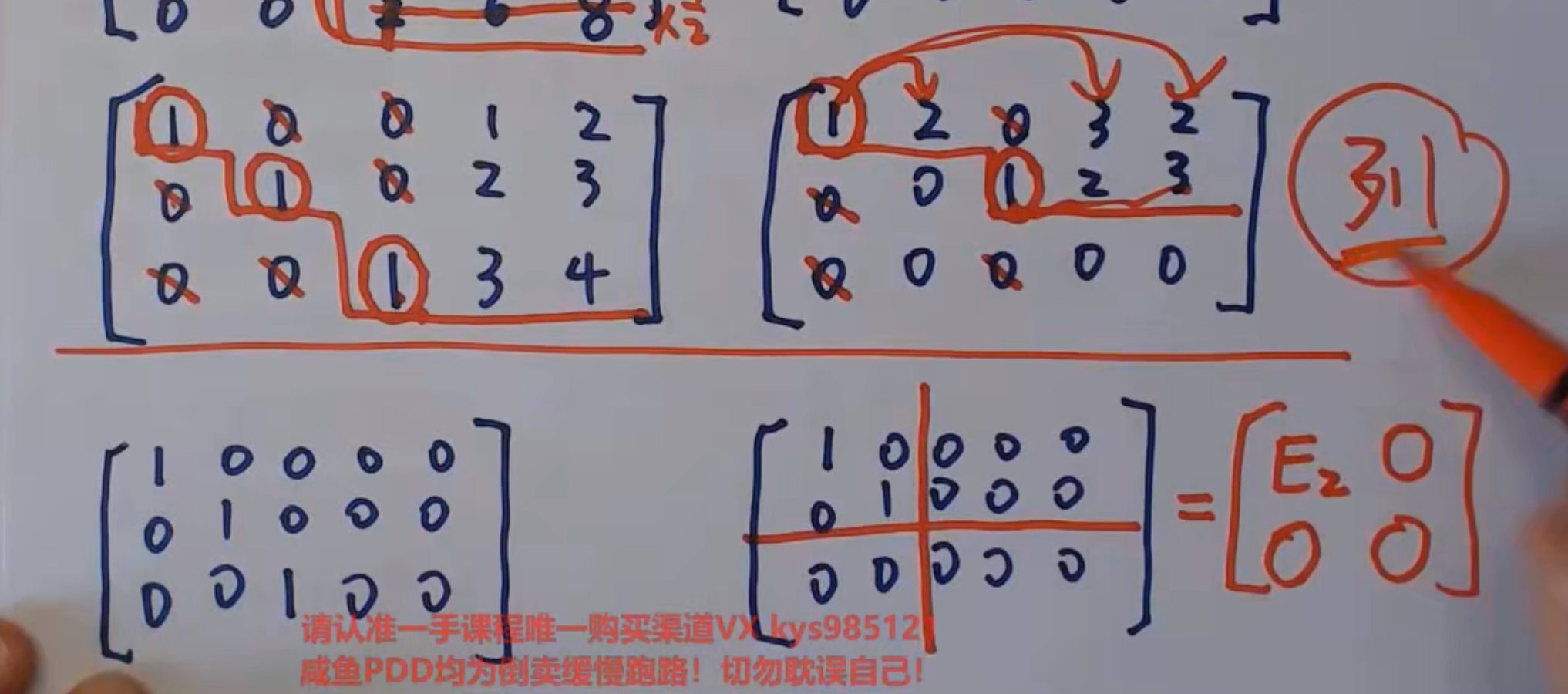
行最简形矩阵
即每个阶梯的开头都是1,并且1的那一列其他元素都是0
而行最简一定能化成标准型
秩的性质和公式

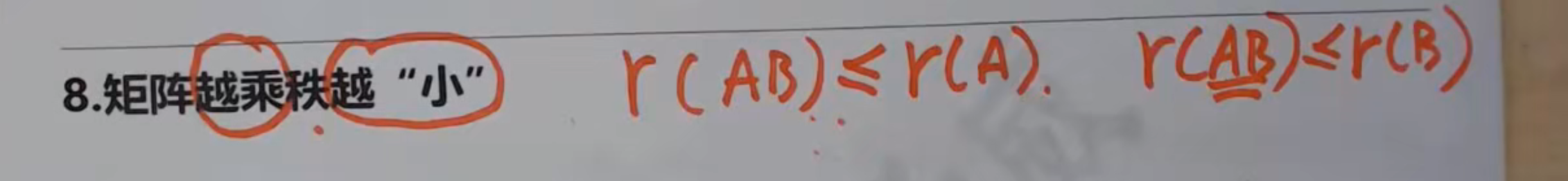


矩阵等价
秩相等即可证明等价,同形矩阵,A经历有限次初等变换得到B即说明二者等价

分块矩阵及其运算
专门注意转置要求改变副对角线的位置

特殊分块矩阵的乘法举例

初等变换求逆矩阵的证明

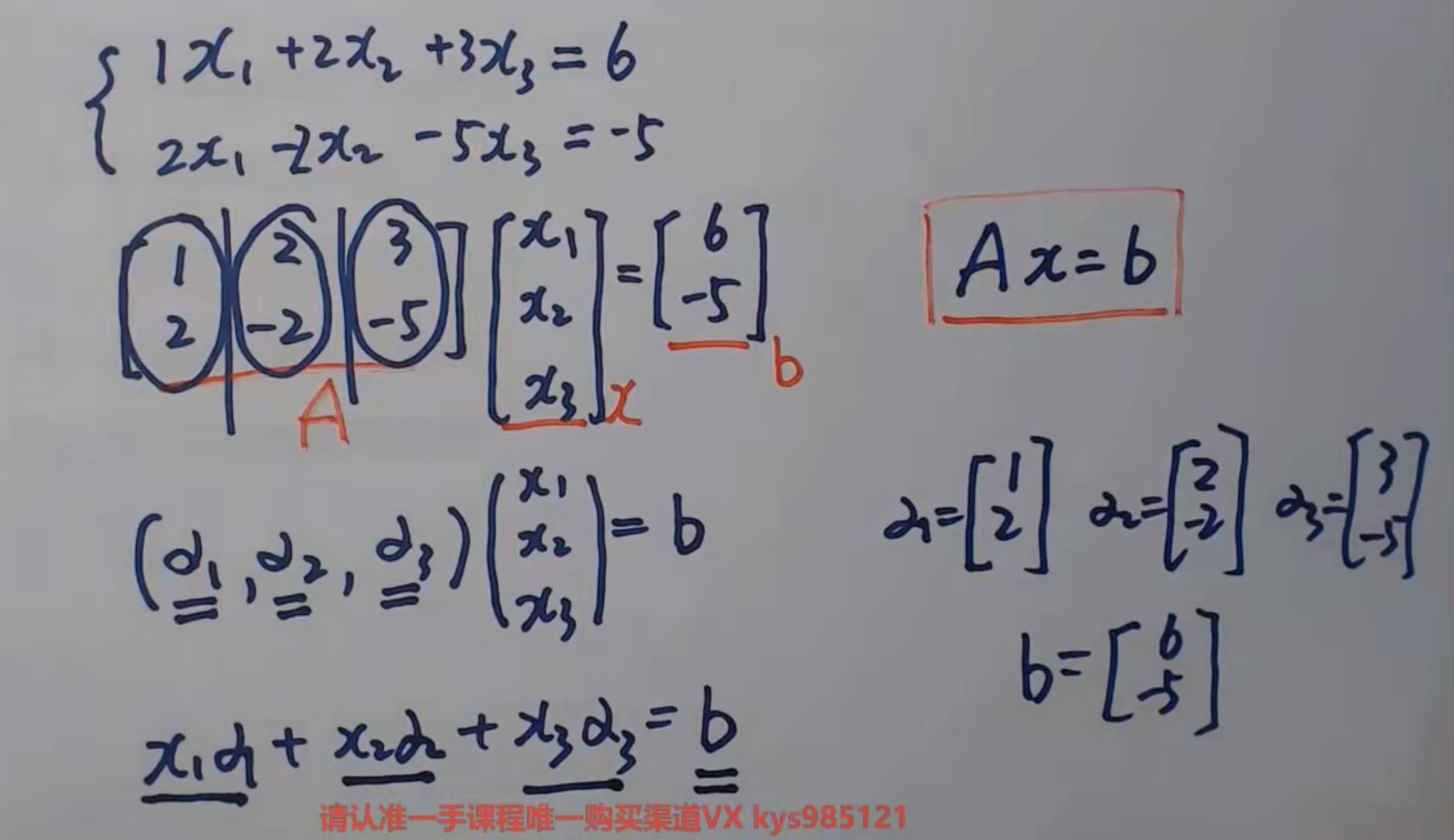

矩阵的运算规律

矩阵幂运算公式

矩阵乘法可交换的情况
其中正交矩阵即A转置等于

伴随运算公式

矩阵与行列式的关系和运算

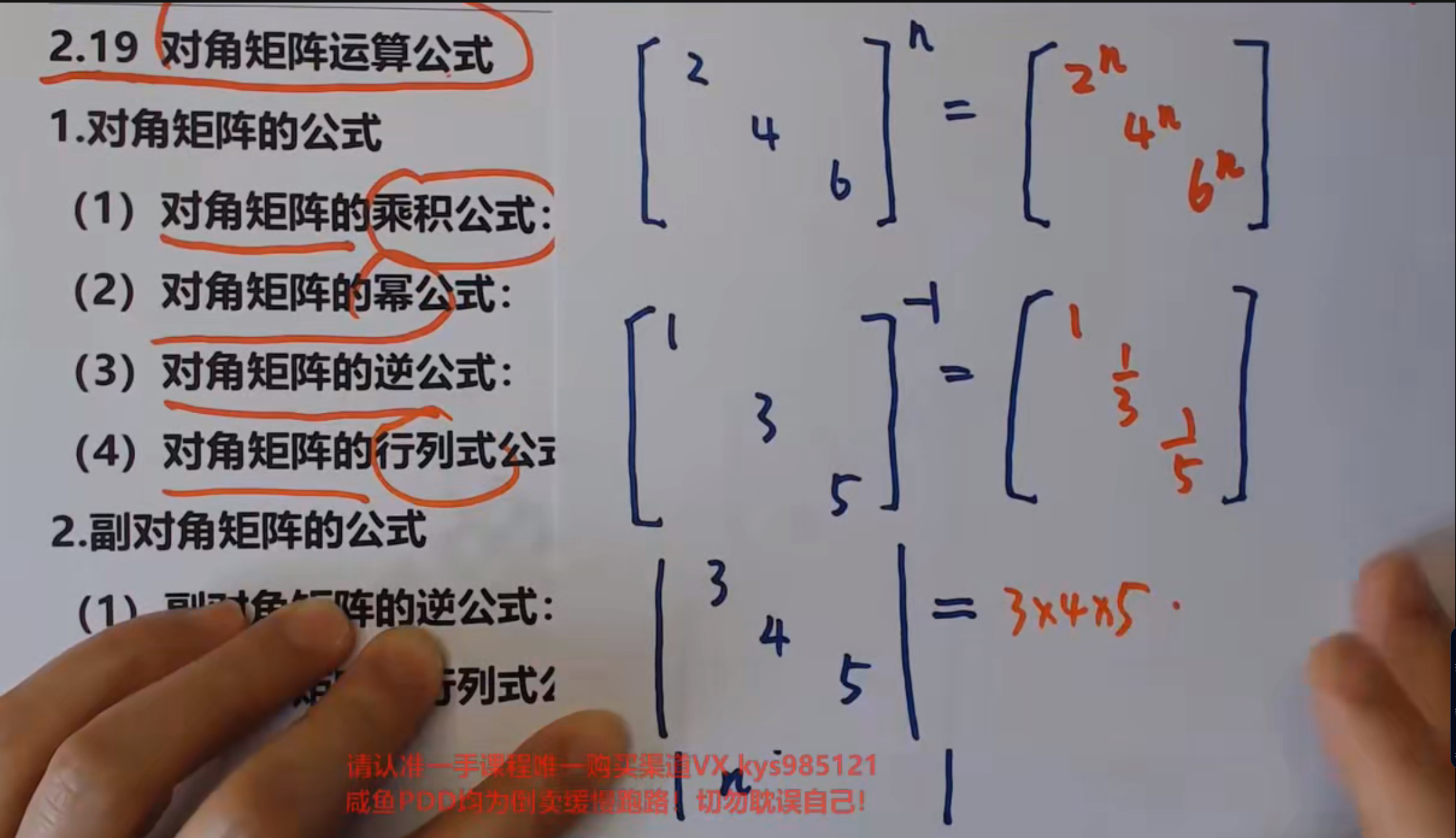
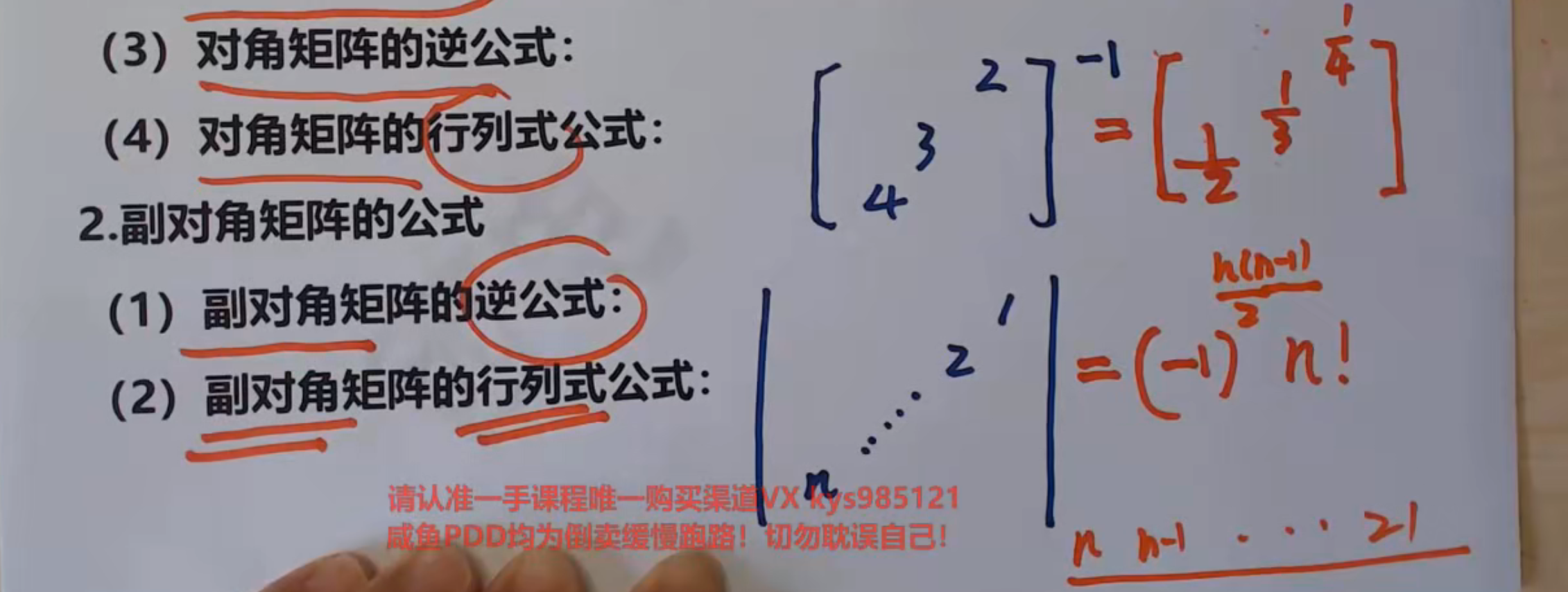
对角矩阵运算公式
对角阵乘积的公式是两个对角线元素相乘即可

副对角
分块矩阵的对角运算
其中主要注意伴随矩阵

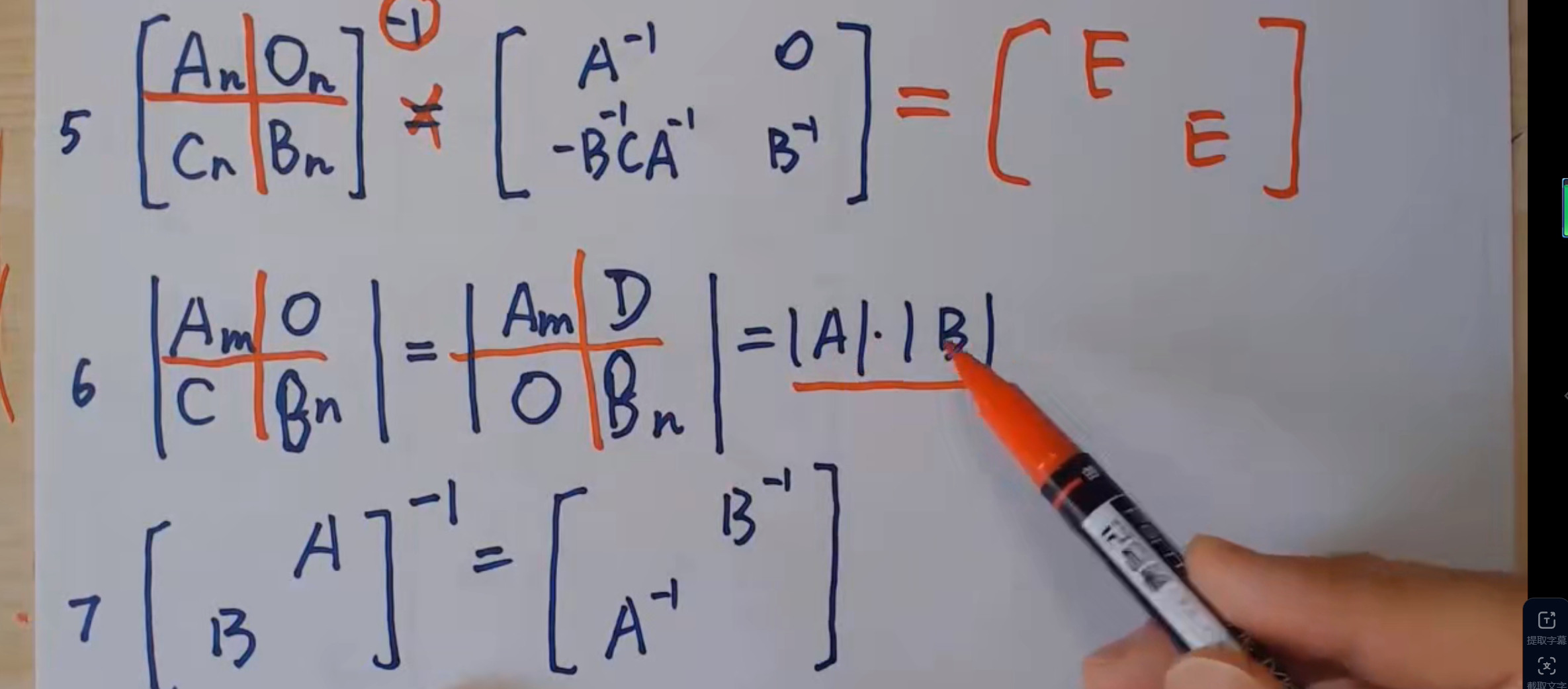
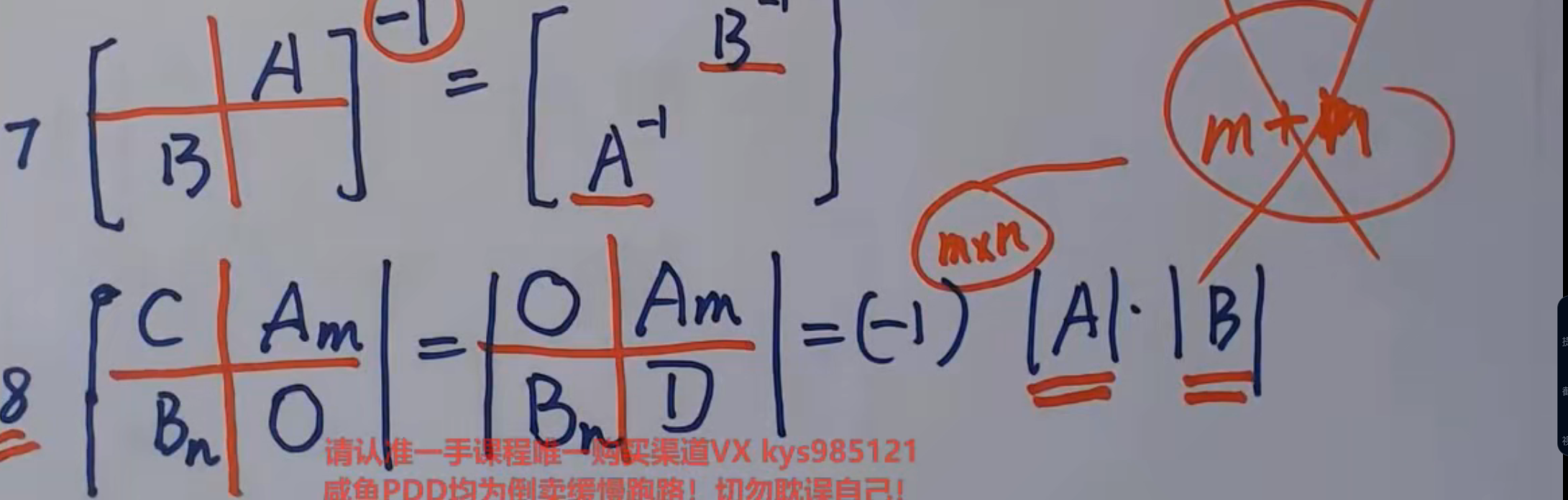
分块矩阵的秩
小矩阵不会>大矩阵
其中5的推导即为,AP本质是A的线性组合,所以行用A经历初等列变换消去AP得到[A,0]
其中可逆矩阵是方阵不会出现列满秩<行数


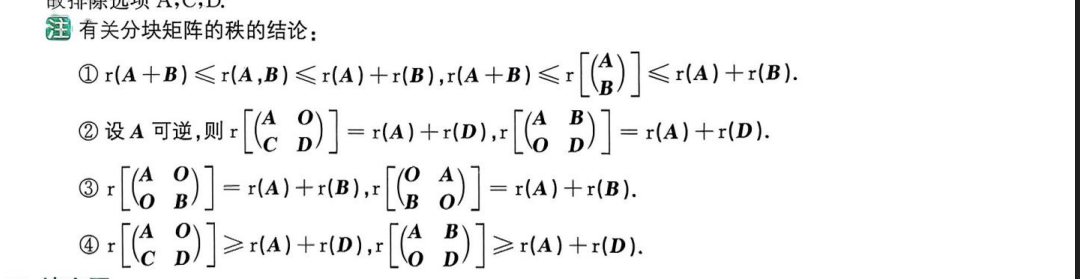
其中最关键的点在于判断出AB相乘之后矩阵的秩变小了,那么就会得到A一定不可逆,因为如果可逆那么就是初等变换那么就不会改变矩阵的秩。

分块矩阵的运算

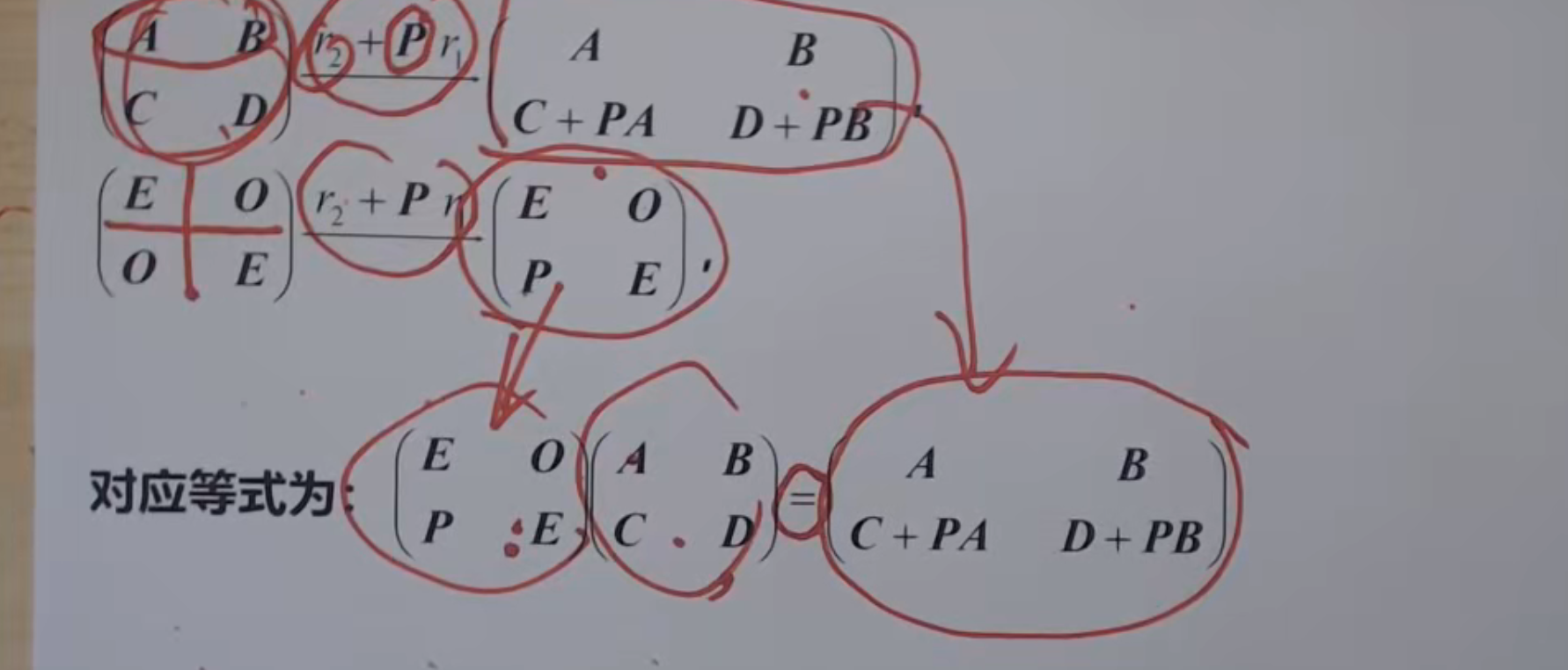
分块矩阵的初等变换


分块初等矩阵的定义

同初等矩阵变换差不多
矩阵和秩的总结





方程组与秩


特征值特征向量与秩

相似矩阵与秩

秩1矩阵的特性

例题
秩1矩阵

三角矩阵主对角为1

矩阵等式恒等变形
只要凭借配凑法配出答案要求的矩阵的逆×多项式,然后右边是单位阵的倍数,即可求得答案

合理将单位矩阵变形成附近的矩阵完成配凑

向量行列变换的关系

西尔韦斯特不等式

高次幂矩阵的总结

对角阵高次幂,分割化为(E+B)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号