详细介绍：算法题（203）：矩阵最小路径和

审题：

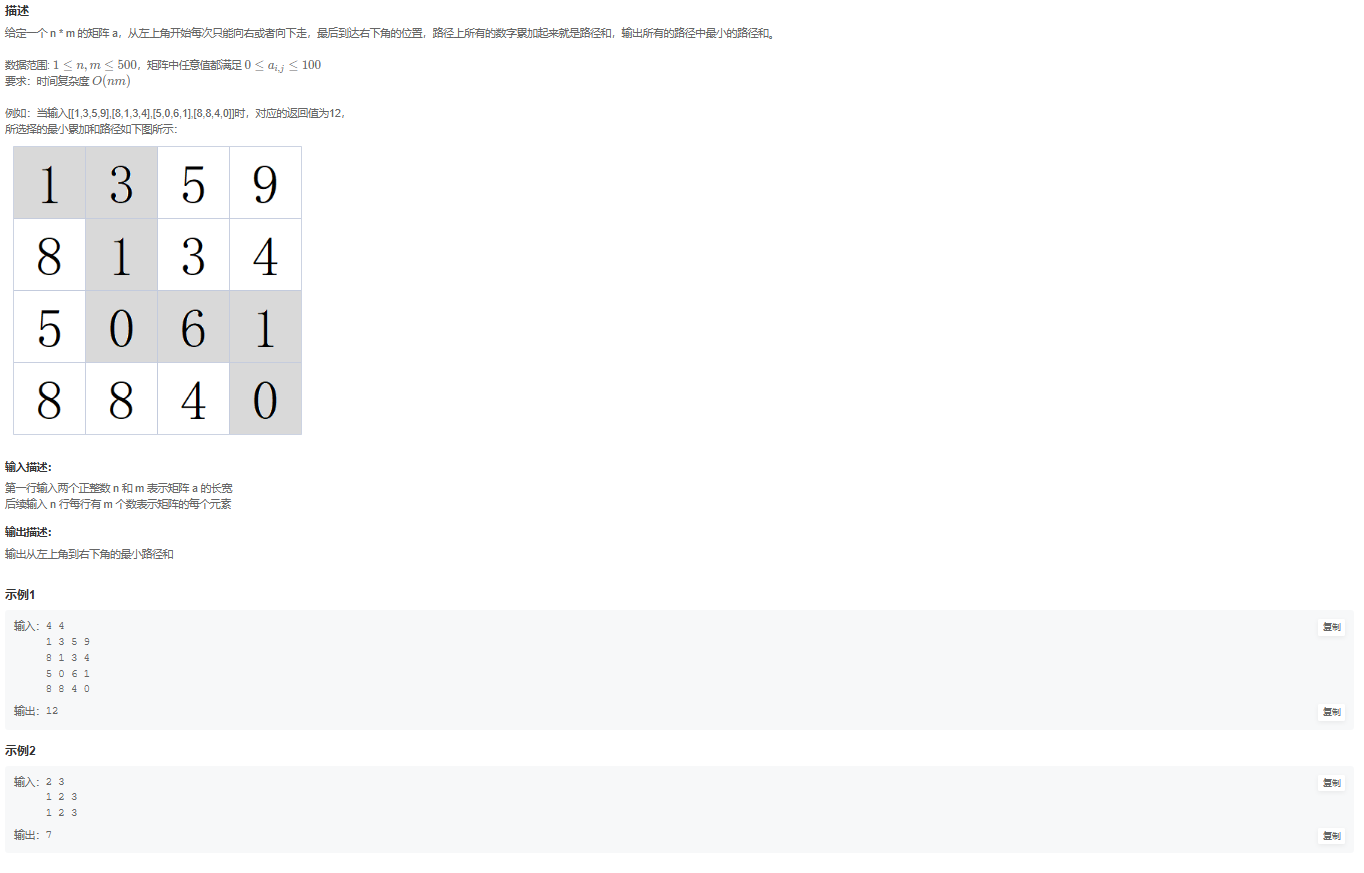
本题需要我们从（1,1）出发，然后通过各种路径走到（n，m）点，并找出所有路径中路径和最小的总和值

思路：
方法一：动态规划

（1）状态表示：f[i][j]表示从（1,1）到达点（i，j）时所有路径中路径和最小的路径值

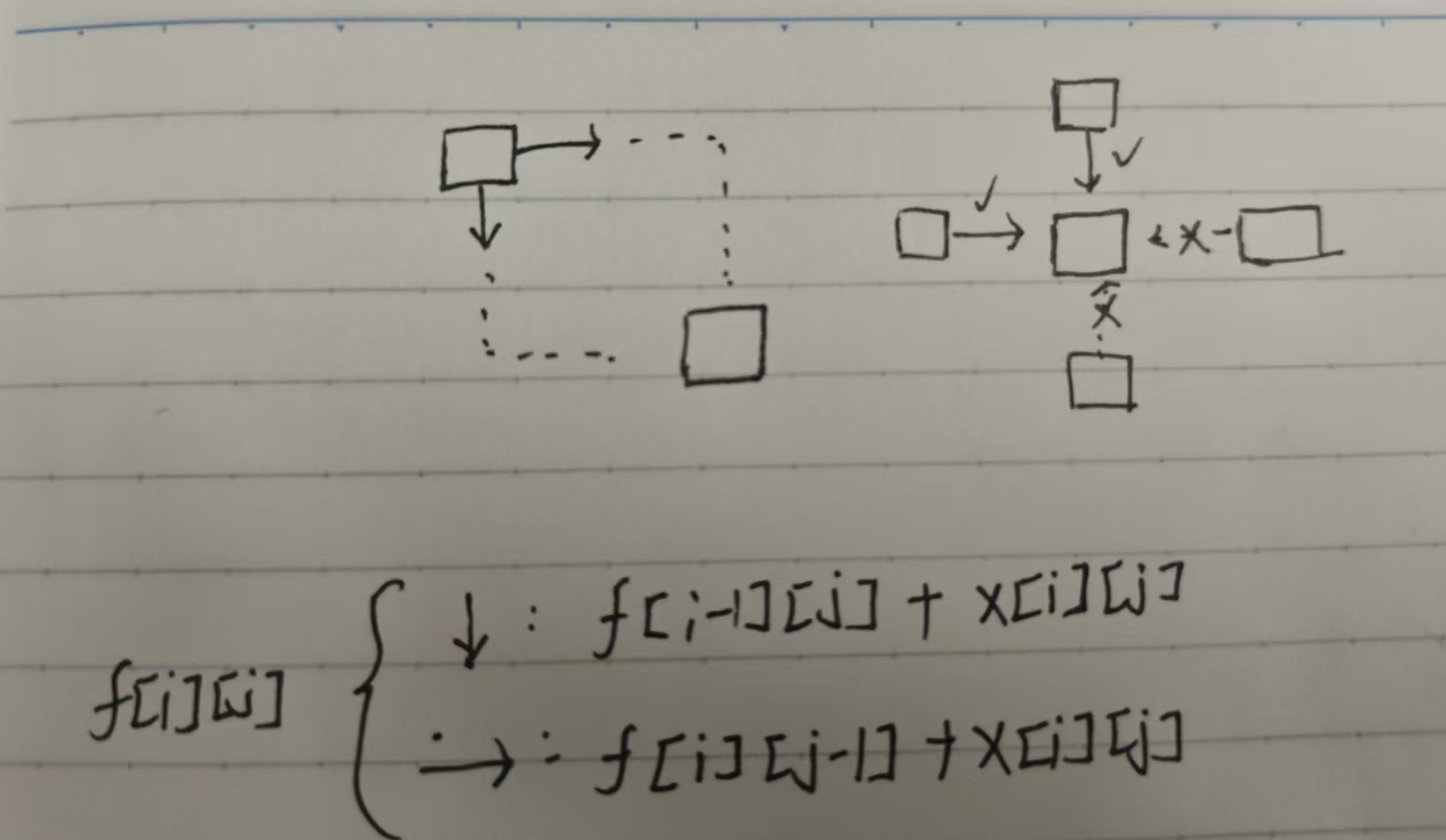
（2）状态转移方程：由于题目中的移动规则是可以向右和向下移动，所以大家的转移方程也是分两种的

图示：

第一种：向下移动

路径和是当前节点的值加上前一个节点的路径总和，即（i-1，j）点的f值加当前节点的值

第二种：向右移动

同理，由（i，j-1）的f值加当前节点的值

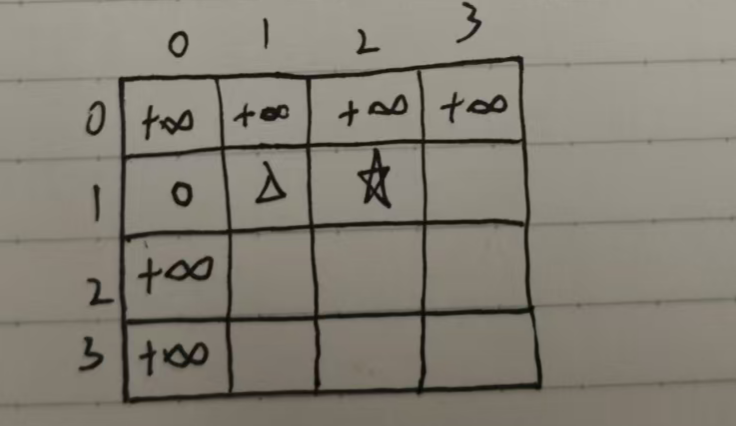
（3）初始化：有两个特殊处理

先，为了确保f[1][1]正确初始化为x[1][1]，我们的f[0][1]/f[1][0]至少有一个初始化为0

图示：

其次，为了防止无效位置妨碍边缘节点的判断，我们的边缘无效位置应该初始化为一个不可能计入最短路径的值，也就是一个max值（0x3f3f3f3f）

图示：

（4）填表顺序：从上到下，从左到右

因为我们某个节点的f需要根据其左方和上方的f求，所以一定要先将上方和左方的f先计算出来

（5）答案输出：直接输出f[n][m]即可

解题：

#include
#include
using namespace std;
const int N = 510;
int n, m;
int x[N][N], f[N][N];
int main()
{
//数据录入
cin >> n >> m;
for (int i = 1; i > x[i][j];
}
}
//初始化
memset(f, 0x3f3f3f3f, sizeof f);
f[1][0] = 0;
//填dp表
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
f[i][j] = min(f[i - 1][j], f[i][j - 1]) + x[i][j];
}
}
//输出数据
cout << f[n][m] << endl;
return 0;
}

memset需要包含cstring头文件才可以使用

矩阵的最小路径和_牛客题霸_牛客网