Part03 数据结构 - 教程

CSP-J 初赛常考知识点总结 - 数据结构篇

1. 图论基础

基本概念与术语

• 边 (Edge)：节点之间的连接线
• 完全图：任意两个顶点之间都有边相连的图
  • $m$ 个节点的完全图边数为：$C_m^2=\frac{m(m-1)}{2}$
• 简单路径：顶点序列中顶点不重复出现的路径
• 连通图：图中任意两个顶点都是连通的（存在路径相连）
  • 注意：完全图一定是连通图，但连通图不一定是完全图

图的分类

• 有向图：边具有方向性（$e=u\to v$）
• 无向图：边没有方向性（$e=u-v$）

环与度

• 环：起点和终点相同的路径，且路径中除起点外无重复顶点
  • 自环：起点和终点相同的边（$e=(u,u)$）
• 入度：以顶点 $v$ 为终点的边的数量
• 出度：以顶点 $v$ 为起点的边的数量

2. 树结构

基本概念

• 树：连通且无环的无向图，具有以下性质：
  • 任意两点间有且仅有一条简单路径
  • 边数 = 顶点数 - 1（$E=V-1$）
  • 形似倒置的树（根在上，叶在下）

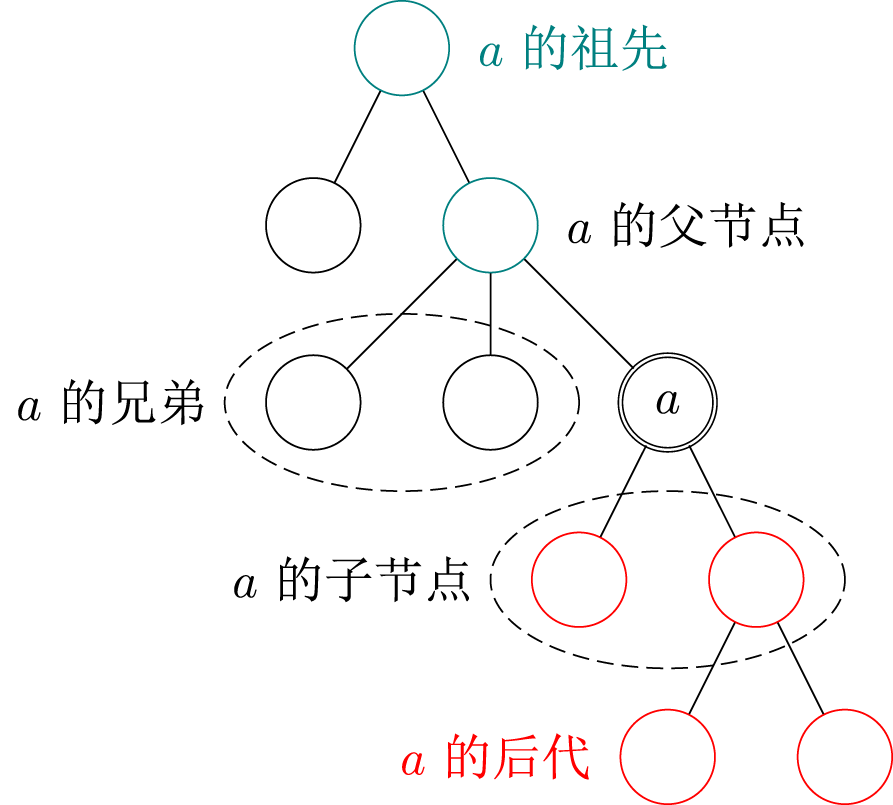
树的术语

• 根结点：树的最顶层节点，每棵树有且仅有一个
• 深度：节点到根结点的路径上的边数
• 高度：所有节点深度的最大值
• 叶结点：没有子结点的结点
• 父结点：除根结点外，每个结点到根路径上的第二个结点
• 祖先：结点到根路径上除自身外的所有结点
• 子结点：如果 $u$ 是 $v$ 的父亲，那么 $v$ 是 $u$ 的子结点
• 兄弟：同一父亲的多个子结点互为兄弟
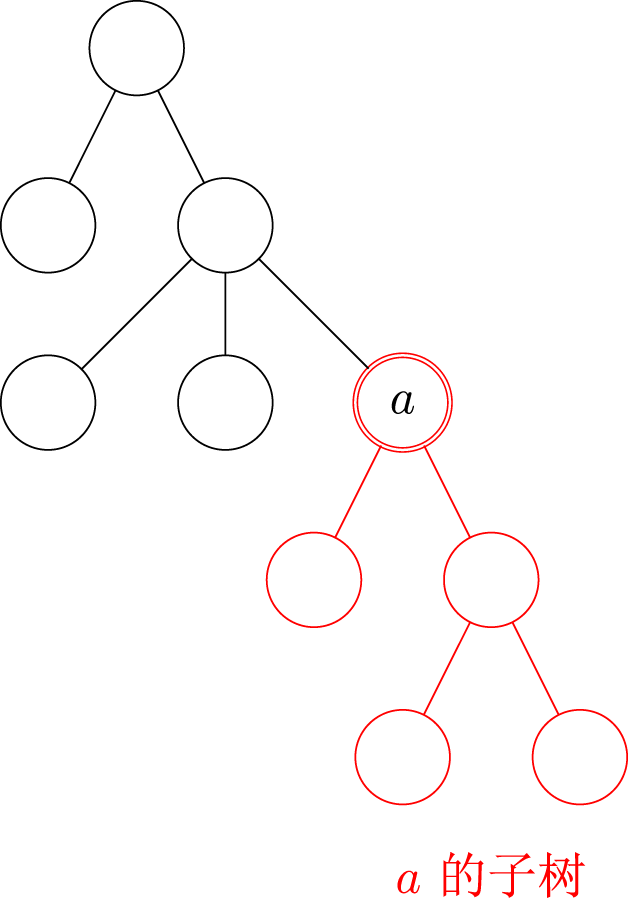
• 子树：删除与父结点相连的边后，该结点所在的子图

## 3. 二叉树

遍历方式

• 前序遍历：根 → 左子树 → 右子树
• 中序遍历：左子树 → 根 → 右子树
• 后序遍历：左子树 → 右子树 → 根

遍历性质

• 前序遍历 + 中序遍历 = 确定唯一二叉树
• 后序遍历 + 中序遍历 = 确定唯一二叉树

### 特殊二叉树

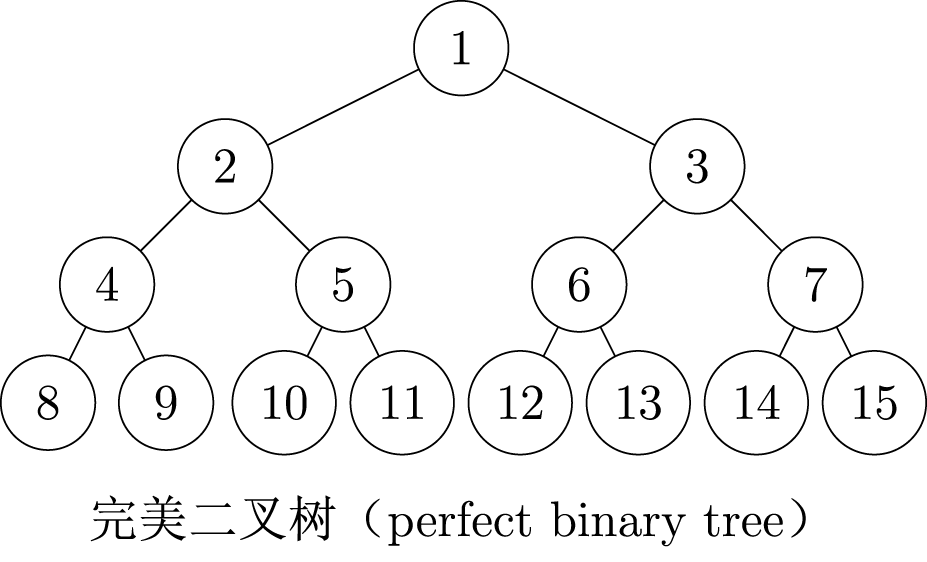
满二叉树/完美二叉树

• 所有叶结点深度相同
• 深度为 $h$ 的满二叉树节点总数为：$2^h-1$
• 叶结点数 $m_0$ 与度为2的结点数 $m_2$ 满足：$m_0=m_2+1$
• 高度为：$\lfloor \log n\rfloor +1$

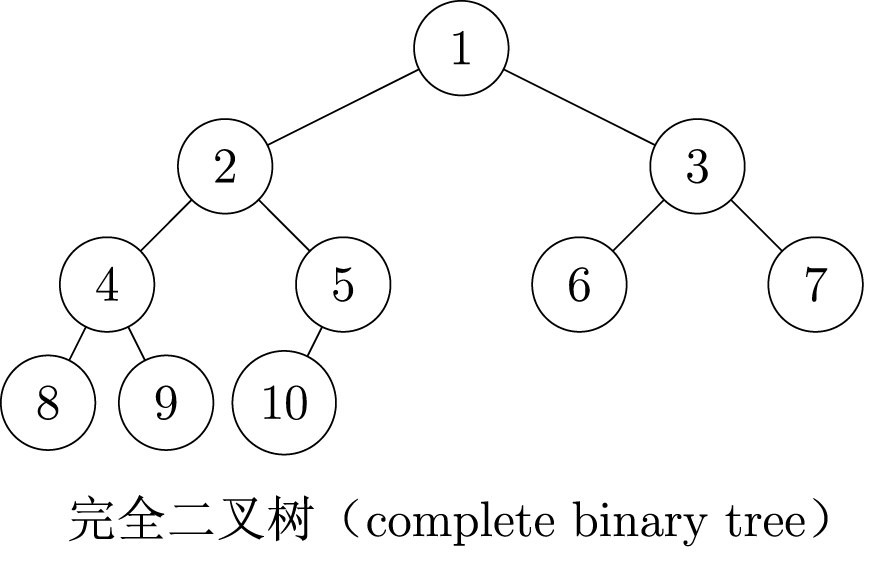
完全二叉树

• 只有最下面两层结点的度数可小于2
• 最下面一层的结点都集中在该层最左边

#### 编号性质

对于满二叉树/完美二叉树/完全二叉树：

• 结点 $i$ 的左儿子编号为：$2i$
• 结点 $i$ 的右儿子编号为：$2i+1$
• 结点 $i$ 的父结点编号为：$\lfloor i/2\rfloor$

4. 栈 (Stack)

定义与特性

• 后进先出 (LIFO) 表：Last In First Out
• 栈顶：栈的最顶端元素
• 栈底：栈的最底端元素

基本操作

操作	功能描述	时间复杂度
push(x)	元素 $x$ 入栈	$O(1)$
pop()	弹出栈顶元素	$O(1)$
top()	返回栈顶元素值	$O(1)$
empty()	判断栈是否为空	$O(1)$
size()	返回栈中元素个数	$O(1)$

5. 队列 (Queue)

定义与特性

• 先进先出 (FIFO) 表：First In First Out
• 队首：队列的第一个元素
• 队尾：队列的最后一个元素

基本操作

操作	功能描述	时间复杂度
push(x)	元素 $x$ 入队	$O(1)$
pop()	队首元素出队	$O(1)$
front()	返回队首元素值	$O(1)$
empty()	判断队列是否为空	$O(1)$
size()	返回队列元素个数	$O(1)$

6. 链表 (Linked List)

特点与性质

• 通过指针连接元素
• 与数组对比：
  • 优点：插入删除操作高效（$O(1)$）
  • 缺点：随机访问效率低（$O(n)$）
• 不支持随机访问：必须从头开始遍历

6.1 STL List 的使用

STL中的list是双向链表容器，基本操作如下：

// 初始化
list<
int> myList;
// 添加元素
myList.push_back(1);
// 在末尾添加
myList.push_front(2);
// 在开头添加
// 删除元素
myList.pop_back();
// 删除末尾元素
myList.pop_front();
// 删除开头元素
// 插入元素
auto it = myList.begin();
advance(it, 1);
// 移动迭代器
myList.insert(it, 3);
// 在指定位置插入
// 删除指定元素
myList.remove(2);
// 删除所有值为2的元素
// 遍历
for (auto it = myList.begin(); it != myList.end();
++it) {
cout <<
*it <<
" ";
}
// 或使用范围for循环
for (int val : myList) {
cout << val <<
" ";
}
// 其他操作
myList.size();
// 返回元素个数
myList.empty();
// 判断是否为空
myList.clear();
// 清空链表

7. 字符串 (String)

基本概念

• 子串：字符串中任意个连续字符组成的子序列
• 长度为 $n$ 的字符串：
  • 所有子串个数：$\frac{n(n+1)}{2}+1$（包含空串）
  • 非空子串个数：$\frac{n(n+1)}{2}$

表达式表示法

前缀表达式（波兰式）

• 运算符在前，操作数在后
• 例：$-+123$ 对应中缀：$1+2-3$

中缀表达式

• 运算符在操作数中间
• 例：$1+2-3$

后缀表达式（逆波兰式）

• 操作数在前，运算符在后
• 例：$12+3-$ 对应中缀：$1+2-3$
• 求值方法：使用栈模拟运算

逆波兰式运算的栈模拟代码

// 假设输入为vector<string>& tokens，包含数字和运算符
  stack<
  int> st;
  for (string token : tokens) {
  if (token == "+" || token == "-" || token == "*" || token == "/") {
  int b = st.top(); st.pop();
  int a = st.top(); st.pop();
  if (token == "+") st.push(a + b);
  else if (token == "-") st.push(a - b);
  else if (token == "*") st.push(a * b);
  else if (token == "/") st.push(a / b);
  } else {
  st.push(stoi(token));
  // 将字符串转换为整数
  }
  }
  int result = st.top();
  // 最终结果

表达式转换方法

方法一：表达式树

1. 构建表达式树（叶节点为操作数，内部节点为运算符）
2. 前序遍历得前缀表达式
3. 中序遍历得中缀表达式
4. 后序遍历得后缀表达式

方法二：加括号法（推荐）

1. 为中缀表达式加括号：$1-2+3\to ((1-2)+3)$
2. 将运算符移到括号前/后
   • 前缀：移到括号前 → $+(-(1,2),3)$
   • 后缀：移到括号后 → $((1,2)-,3)+$
3. 删除括号得最终表达式

习题参考

• CSP 2019 入门组第一轮-T6：链表应用
• CSP 2019 入门组第一轮-T8：二叉树性质

---

CSP-J 入门组复习大纲

• 2.1.1 基础知识与编程环境
• 2.1.2 C++ 程序设计
• 2.1.3 数据结构
• 2.1.4 算法
• 2.1.5 数学
• 2.1.6 其他杂项