元胞自动机（Cellular Automata, CA） - 指南

一、什么是元胞自动机（Cellular Automata, CA）

元胞自动机（CA） 是一种基于离散时间、离散空间与规则驱动演化的动力系统，由 冯·诺依曼（John von Neumann） 于1940年代首次提出，用于模拟生物自我复制行为。

：就是其基本思想

系统中每个元胞（cell）根据自身状态与邻域状态，依据某一组固定规则，在每一轮迭代中更新自己的状态，整个系统因此展现出复杂的宏观格局演化特征。

经典定义（Wolfram, 1983）：

A cellular automatonis adiscrete model consisting of a regular grid of cells, each in one of a finite number of states, updated in discrete time steps according to a local rule.

二、元胞自动机模型的根本结构

元胞自动机环境通常包含以下 4 个核心组成部分：

要素	描述
空间结构	通常为规则格网（二维栅格），也可以扩展到六边形或三维空间
状态集合	每个格子（cell）拥有一个状态（如 0/1 表示是否建成，或土地类型编码）
邻域结构	描述某个元胞周围哪些格子参与演化（如摩尔邻域 8 邻、冯·诺依曼邻域 4 邻）
转移规则	一个映射函数：当前状态 + 邻域状态 → 下一状态，可能是确定的也可能是概率的

三、CA 在地理模拟中的引入

在地理学中，**Batty 和 Xie（1994）**首次将 CA 模型系统性地应用于城市增长模拟。他们指出：

“Urban systems are dynamic and complex, but CA provides a simple and intuitive structure to simulate their evolution.”
—— Batty & Xie (1994), Environment and Planning B

四、元胞自动机概述

1．元胞自动机的基本组成
元胞自动机的数学模型由以下核心组件构成：

网格（Grid）：

元胞自动机定义在一个离散的网格上，通常是一维（线形）、二维（平面）或更高维的网格。每个网格点称为一个元胞（cell）。

数学上，网格可能表示为整数坐标集，例如一维网格为Z ，二维网格为Z2 。

每个元胞有一个有限的状态集S ，例如二元状态S={0,1}（如＂开＂或＂关＂）或多状态（如气温范围）。

状态（State）：

每个元胞在时间t 具有一个状态si(t)∈S ，其中i 表示元胞的位置。

整个网格的状态称为配备（configuration），用函数C(t):Zd→S 表示，其中d网格维度。就是

邻居（Neighborhood）：

每个元胞的下一状态取决于其自身及其邻居的状态。邻居的定义依赖于网格类型和规则，例如：

一维：常用邻居包括左右相邻元胞（Von Neumann 邻域）或更广的范围。

二维：常见邻居包括 Von Neumann 邻域（上下左右4个元胞）或 Moore 邻域（包括对角线共 8个元胞）。

数学上，邻域能够定义为一个元胞的索引集Ni ，表示影响元胞i 的邻居集合。

转移规则（Transition Rule）：

转移规则是一个函数f:S|N|→S ，决定元胞在下一时间步的状态。

对于元胞 i ，其状态更新公式为：

si(t+1)=fsj1(t),sj2(t),…,sj∣N(t),

其中 j1,j2,…,j|N|∈Ni 是邻居索引。

时间演化：
时间是离散的，记为t=0,1,2,… 。在每个时间步，所有元胞根据转移规则同步更新状态，形成新的部署C(t+1) 。
－全局演化可以看作一个映射F:SZd→SZd ，将当前配置映射到下一配置。
2．数学原理
元胞自动机的数学原理许可从以下几个方面分析：
（1）离散动力系统
－元胞自动机是一个离散时间、离散空间的动力系统。全局配置空间SZd 是一个无限维的状态空间，转移规则F 定义了一个确定性映射。
－数学上，元胞自动机的演化可以表示为：

C(t+1)=F(C(t))

通过－这种迭代映射能够生成复杂的动态行为，包括固定点、周期循环、混沌等。
（2）局部性与全局性
－元胞自动机的核心数学特性是局部规则生成全局行为。尽管转移规则f 仅依赖于局部邻居状态，但依据同步更新，整个系统可以表现出复杂的模式，如自组织、涌现现象等。
通过－例如，在一维元胞自动机中，规则能够定义为：

si(t+1)=fsi-1(t),si(t),si+1(t)

对于二元状态S={0,1} ，可能的规则数为 223=256（如著名的 Wolfram 规则编号）。

（3）规则的数学表达
－转移规则 f 通常是确定性的，但可以是任意函数。例如，在 Conway 的生命游戏（二维元胞自动机）中，状态S={0,1} ，规则为：

存活（1）：若一个元胞为 1，且其 Moore 邻域中有 2 或 3 个活元胞，则下一时刻仍为 1。
死亡（ 0 ）：若活元胞邻居少于 2 （孤立）或多于 3 （过挤），则变为 0 。
出生（1）：若死元胞（0）有正好 3 个活邻居，则变为 1。
数学表达为：

si(t+1)=1 if si(t)=1 and j∈Nisj(t)∈{2,3}1 if si(t)=0 and j∈Nisj(t)=30 otherwise

（4）不变性与对称性

元胞自动机的规则通常具有空间平移不变性，即规则f 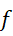在网格上对所有元胞一致应用。
某些规则还具有时间对称性或可逆性，即存在反向规则使得体系可回溯（常见于物理模拟）。
数学上，平移不变性意味着对于任意平移变换τ ，有F(τ(C))=τ(F(C)) ，其中τ 是网格上的平移运算。
（5）计算复杂性
－元胞自动机与计算理论密切相关。某些元胞自动机（如 Wolfram 的 Rule 110）被证明是图灵完备的，即它们允许模拟通用图灵机，执行任意计算。
－数学上，设置空间SZd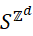 是一个 Cantor 集，转移规则F 是一个连续映射（在适当的拓扑下）。繁琐行为的涌现可以凭借熵或李雅普诺夫指数等量来分析。

五、典型模型扩展与集成方式

CA-Markov 模型
将 CA 与马尔科夫链结合，预测未来土地状态转移概率 + 空间演化

Eastman, 2006. IDRISI Manual.

SLEUTH 城市扩张模型
集成了 Slope、Landuse、Exclusion、Urban、Transportation、Hillshade 六因子

Clarke et al., 1997. “A self-modifying cellular automaton model of historical urbanization...”

CA-RF / CA-ANN
将机器学习（随机森林、神经网络）与 CA 融合，自动学习转移概率，提高预测精度

Zhang et al., 2018. “Integrating cellular automata and random forest...”

六、元胞自动机的优点与局限性

✅ 优点：

模型结构简单，计算高效，逻辑直观

与遥感栅格、GIS 空间数据天然兼容

可模拟空间自组织、扩散与边界演化

❌ 局限性：

传统规则往往静态，缺乏学习与适应性

难以建模非局域过程（如政策驱动）

参数敏感，依赖专家经验或反复校准

七、研究趋势与发展方向

智能 CA：与机器学习融合（CA-RF, CA-ANN）自动学习规则

多主体模型集成：模拟居民、开发商行为（CA + ABM）

多尺度建模：宏观土地转移 + 微观邻域演化

GEE + CA集成：基于大尺度遥感数据动态建模（MODIS + CA）


import numpy as np
importmatplotlib.pyplotas plt
 
# 设置参数
size =50 # 网格大小 50x50
steps =20 # 模拟步数
threshold =3 # 至少有多少城市邻居才能考虑转化
probability =0.6 # 转化为城市的概率
 
# 初始化格网
grid = np.zeros((size, size), dtype=int)
# 初始化种子城市（中心点）
grid[size//2, size//2] = 1
 
# 8邻域方向（Moore 邻域）
neighbors = [(-1, -1), (-1, 0), (-1, 1),
 (0, -1), (0, 1),
 (1, -1), (1, 0), (1, 1)]
 
# 演化函数
def update(grid):
new_grid = grid.copy()
 for i in range(1, size-1):
 for j in range(1, size-1):
 ifgrid[i, j] ==0:
count =sum(grid[i+dx, j+dy]fordx, dyinneighbors)
 ifcount >= thresholdandnp.random.rand() < probability:
new_grid[i, j] =1
 returnnew_grid
 
# 逐步模拟
for step in range(steps):
plt.imshow(grid, cmap='Greys')
plt.title(f'Step{step}')
plt.pause(0.3) # 暂停显现
grid = update(grid)
 
plt.show()

posted on 2025-06-04 07:46 ljbguanli 阅读(874) 评论(0) 收藏举报