python分析中国五大城市的PM2.5值
数据分析-用python分析中国五大城市的PM2.5值(ols建立回归模型)
文章目录
分析目的
观察数据
数据清洗
数据整合
数据分析
分析目的
细颗粒物又称PM2.5,指环境空气中空气动力学当量直径小于等于2.5微米的颗粒物。它能较长时间悬浮于空气中,其在空气中含量浓度越高,就代表空气污染越严重。此次分析的目的是通过各城市的气象信息预测该城市的pm2.5值,具体气象信息包含空气湿度、温度等。
观察数据
这个小时数据集包含北京、上海、广州、成都和沈阳的PM2.5数据。同时,还包括各城市的气象资料。

数据清洗
观察数据可以看出每张表都有各自城市分区的pm值,这些值的缺失值较多,而且此次分析的重点是研究整个城市的pm值,因此将这些分区属性数据还有其他有缺失值的元组数据都删掉;同时数据中有no一列,该属性对此次的研究也没有意义,也应该删掉。
数据整合
将五张表都添加城市列,然后整合成一张总表。总表包含的分类变量有年(year)、月(month)、天(day)、小时(hour)、季节(season)、风向(CBWD)、城市(city);连续变量有PM值(PM_US
Post)、露点(DEWP)、湿度(HUMI)、压力(PRES)、温度(TEMP)、累计风速(Iws)、降水量(precipitation)、累计降水量(Iprec)。
数据分析
数据预览
pm.info()

这份数据共有161630条观则。
连续变量描述
pm1=pm[['PM_US Post','DEWP','HUMI','PRES','TEMP','precipitation']]
pd.set_option('display.max_columns',500)#全部显示
pm1.describe()
pm1['PRES'].skew()#计算数据的偏度
pm1['PRES'].kurt()#计算数据的峰度

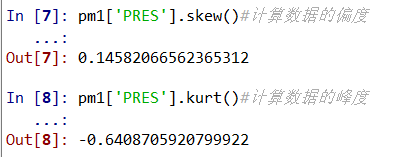
这五个城市有记录的PM值的均值近似为74,中位数为54,均值大于中位数值,说明此列数据呈右偏分布。同样呈右偏分布的还有降水量(precipitation)的值,但右偏幅度很小。相反,这五个城市有记录的露点(DEWP)、湿度(HUMI)、温度(TEMP)三列的值分别的均值均小于各自的中位数,则说明这三列数据都呈左偏分布,幅度较小。较特殊的是压力(PRES)列的值,它的中位数和均值相等,因此需要对对压力做偏度和峰度检验,由检验结果可以看出,偏度为0.14582,峰度为-0.64087,与0都相差不大,故可以将此列数据看作近似服从正态分布。
分季节观察
import matplotlib.pylab as plt
spring=pm[(pm["season"]==1)]
gp1=spring.groupby(['year','city'])['PM_US Post']
gp1.size()
gpa1=gp1.mean()
gpa1=gpa1.unstack()
gpa1.plot(kind='bar',figsize=(6,4))
plt.title('Spring PM value')
plt.xlabel('year')
plt.ylabel('PM_US Post')
plt.show()
summer=pm[(pm["season"]==2)]
gp2=summer.groupby(['year','city'])['PM_US Post']
gp2.size()
gpa2=gp2.mean()
gpa2=gpa2.unstack()
gpa2.plot(kind='bar',figsize=(6,4))
plt.title('Summer PM value')
plt.xlabel('year')
plt.ylabel('PM_US Post')
plt.show()
autumn=pm[(pm["season"]==3)]
gp3=autumn.groupby(['year','city'])['PM_US Post']
gp3.size()
gpa3=gp3.mean()
gpa3=gpa3.unstack()
gpa3.plot(kind='bar',figsize=(6,4))
plt.title('Autumn PM value')
plt.xlabel('year')
plt.ylabel('PM_US Post')
plt.show()
winter=pm[(pm["season"]==4)]
gp4=winter.groupby(['year','city'])['PM_US Post']
gp4.size()
gpa4=gp4.mean()
gpa4=gpa4.unstack()
gpa4.plot(kind='bar',figsize=(6,4))
plt.title('Winter PM value')
plt.xlabel('year')
plt.ylabel('PM_US Post')
plt.show()
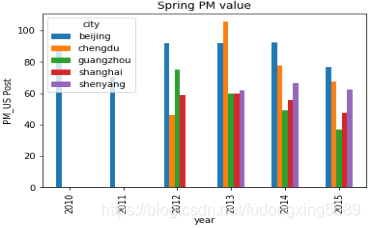
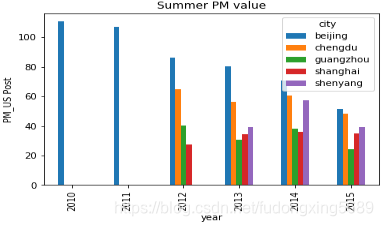
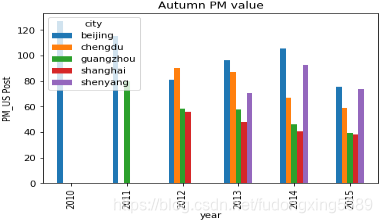

数据主要集中在2012年到2015年,且春季和冬季的PM值要比夏季和秋季的PM值要大,说明春季的冬季的污染情况较为严重。总体来看,无论是哪个季节,总体的PM值都有随年份减小的趋势,说明污染在减缓。
以风向分组统计pm均值
mypivot=pd.pivot_table(pm,index=['city'],values=['PM_US Post'],columns=['cbwd'],aggfunc=[np.mean])
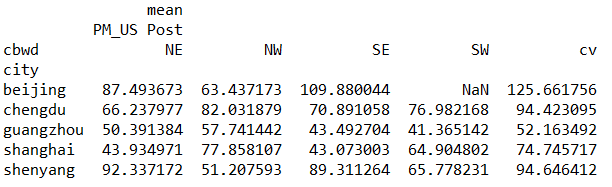
通过以城市为行索引,组合方向为列索引,PM的均值为值建立数据透视表如上,整体上看,当风向为cv时,各城市的PM值都相对较大。
计算连续变量相关系数
pm2=pm[['PM_US Post','DEWP','HUMI','PRES','TEMP','Iws','precipitation','Iprec']]
pm2.corr()
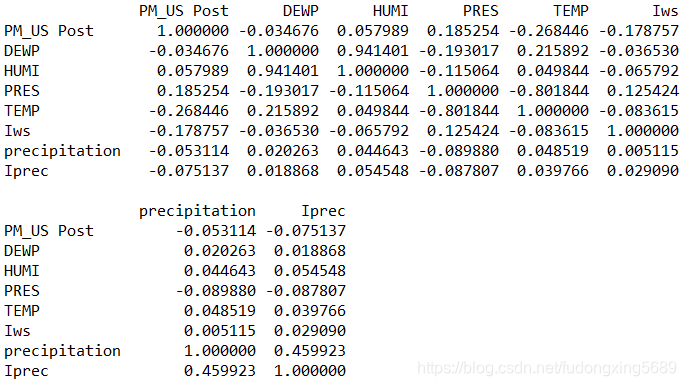
变量PM_US
Post和变量DEWP、变量HUMI、变量precipitation以及变量Iprec的相关系数都很小,分别为-0.034676,0.057989,-0.053114和-0.075137;变量DEWP和变量HUMI的相关系数较大,为0.941401,变量PRES和变量TEMP的相关系数较大,为-0.801844,变量precipitation和变量Iprec的相关系数也较大,为0.459923,这些相关系数较大的变量应避免同时存在在回归模型中。
最小二乘回归
提取数据集中的年(year)、季节(season)、风向(CBWD)、城市(city)、PM值(PM_US
Post)、温度(TEMP)、累计风速(Iws)共七个变量,并将年(year)、季节(season)、风向(CBWD)、城市(city)四个分类变量建立虚拟编码,将70%的数据作为训练集,30%的数据作为测试集建立回归模型。
pm3=pm[['year','season','PM_US Post','TEMP','cbwd','Iws','city']]
pm4=pd.get_dummies(pm3,columns=['year','season','cbwd','city'])#建立虚拟编码
train=pm4.sample(frac=0.7)
test=pm4[~pm4.index.isin(train.index)]
xtrain,ytrain=train.drop('PM_US Post',axis=1),train['PM_US Post']
xtest,ytest=test.drop('PM_US Post',axis=1),test['PM_US Post']
import statsmodels.api as sm
xtrain=sm.add_constant(xtrain)#添加常数项
xtest=sm.add_constant(xtest)
results=sm.OLS(ytrain,xtrain).fit()
print(results.summary())
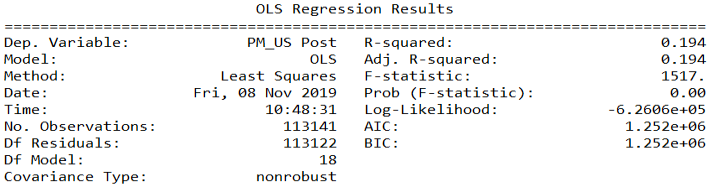
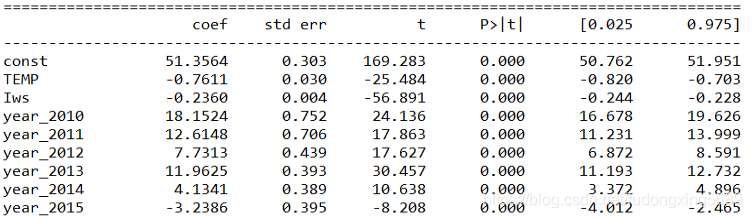
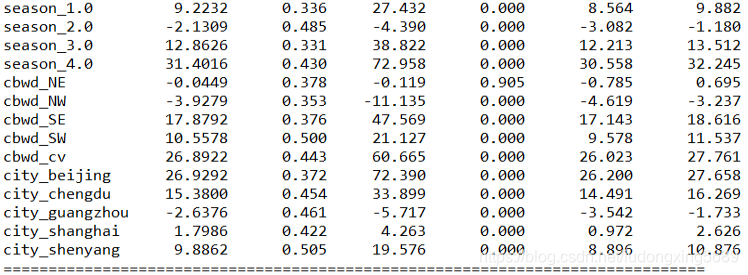
回归后,我们发现回归后原数剧和预测结果的相关系数很小,为0.194,故回归效果不好。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号