贪心day1
53. 最大子数组和
class Solution {
public int maxSubArray(int[] nums) {
int count = 0, res = Integer.MIN_VALUE;
int len = nums.length;
for (int i = 0; i < len; i++) {
count += nums[i];
//取到比前面最大值还大的值
if (count > res) res = count;
//如果前面和为负数,那么对只会是累赘,便从i+1开始计数
if (count < 0) count = 0;
}
return res;
}
}
亦可以使用动规解之
//动规
class Solution {
public int maxSubArray(int[] nums) {
int len = nums.length;
int[] dp = new int[len];
dp[0] = nums[0];
int res = dp[0];
for (int i = 1; i < len; i++) {
//记录到i的最大连续子序列和
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
res = Math.max(res, dp[i]);
}
return res;
}
}
分治法 对大量数据处理较优秀 可以取到任意区间的最大子数组和。
//分治 线段树
class Solution {
private class Status {
int iSum; //[l, r]总和
int lSum; //[l, r]以l为端点的最大子数组和
int rSum; //r为端点
//求mSum需要子结点由子结点lSum 和 rSum求得
int mSum; //[l, r]中最大子数组和
public Status(int iSum, int lSum, int rSum, int mSum) {
this.iSum = iSum;
this.lSum = lSum;
this.rSum = rSum;
this.mSum = mSum;
}
}
public int maxSubArray(int[] nums) {
return getInfo(nums, 0, nums.length - 1).mSum;
}
private Status pushUp(Status l, Status r) {
int iSum = l.iSum + r.iSum; //由子区间总和得来
//左子区间左端最大数组和 与 左左区间总和+右子区间左端最大数组和
int lSum = Math.max(l.lSum, l.iSum + r.lSum);
int rSum = Math.max(r.rSum, r.iSum + l.rSum);
//左区间右端+右区间左端 左区间最大和 由区间最大和 取最大
int mSum = Math.max(l.rSum + r.lSum, Math.max(l.mSum, r.mSum));
return new Status(iSum, lSum, rSum, mSum);
}
private Status getInfo(int[] nums, int l, int r) {
//[l, r]只有一个元素了,不能继续分
if (l == r) {
return new Status(nums[l], nums[l], nums[l], nums[l]);
}
int m = (l + r) / 2;
Status lInfo = getInfo(nums, l, m);
Status rInfo = getInfo(nums, m + 1, r);
return pushUp(lInfo, rInfo);
}
}
122. 买卖股票的最佳时机 II
动规解法,可恶一开始思路就是动规,贪心存在感太低了
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
//只有一天,当天卖出利润为0
if (len == 1) return 0;
int[] dp = new int[len];
dp[0] = 0;
int res = 0;
for (int i = 1; i < len; i++) {
dp[i] = 0;
if (prices[i] > prices[i - 1]) {
//因为dp[i]由dp[i - 1]得来,也可以定义一个变量 而不用定义dp数组进行维护
dp[i] = dp[i - 1] + prices[i] - prices[i - 1];
//到了可买天数最后一天
if (i == len - 1) res += dp[i];
//如果发现当前比前一天股价低,则卖出
} else if (prices[i] <= prices[i - 1]) {
res += dp[i - 1];
}
//System.out.println(res);
}
return res;
}
}
动规2
class Solution {
public int maxProfit(int[] prices) {
int res = 0;
int len = prices.length;
//记录买入时刻
int pre = prices[0];
for (int i = 1; i < len; i++) {
//卖出时机
if (prices[i] < prices[i - 1]) {
res += prices[i - 1] - pre;
pre = prices[i];
} else if (i == len - 1) {
//最后一个交易日也应出售
res += prices[i] - pre;
}
}
return res;
}
}
贪心,思路很巧妙
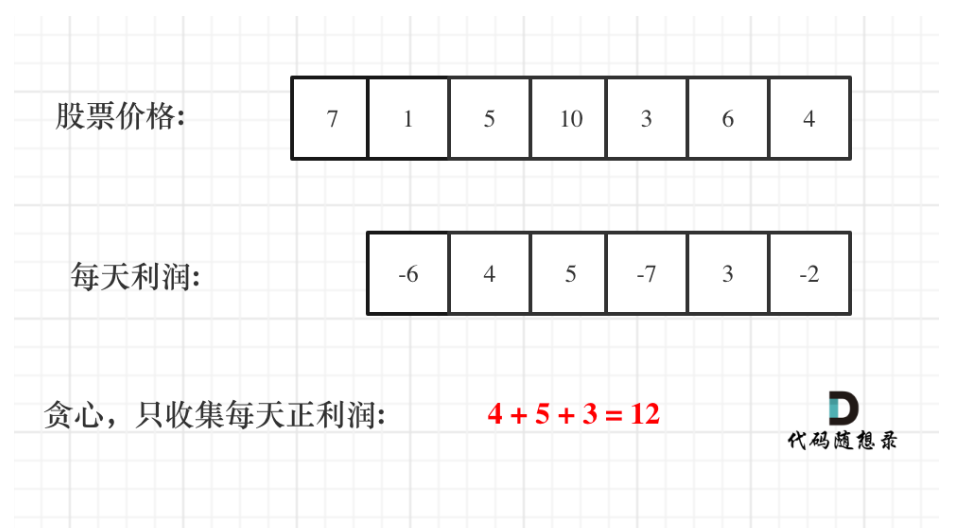
卡哥牛的
//贪心
class Solution {
public int maxProfit(int[] prices) {
int res = 0;
for (int i = 1; i < prices.length; i++) {
//有利润就卖
res += Math.max(prices[i] - prices[i - 1], 0);
}
return res;
}
}
看了官解,感觉自己的动规是野生动规。服了
//正版动规
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if (len == 1) return 0;
//dp[i][0]为第i天不持股票时剩的现金
//dp[i][1]为第i天持有股票时剩的现金
int dp[][] = new int[len][2];
//第0天,不持股票现金不变,持股就要买入 减去当前股价prices[0]
dp[0][0] = 0;
dp[0][1] -= prices[0];
for (int i = 1; i < len; i++) {
//第i天 dp[i][0]:1.i-1天持股今天卖掉;2.i-1天不持股就无动作 由这两种情况结果中取最大值
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
//dp[i][1]:1.i-1天不持股今天买入;2.i-1天持股(最多只能持有一支股票)
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[len - 1][0];
}
}
其状态转移方程

作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/solution/mai-mai-gu-piao-de-zui-jia-shi-ji-ii-by-leetcode-s/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
参考:1.programmercarl.com




 浙公网安备 33010602011771号
浙公网安备 33010602011771号