动态规划day02

343. 整数拆分

class Solution {
    public int integerBreak(int n) {
        if (n < 2) return -1;
        int dp[] = new int[n + 1];
        dp[2] = 1;
        for (int i = 3; i <= n; i++) {
            //dp[i - j]没有dp[0]和dp[1]的情况，而i - j = 1的情况与j = 1的情况相同，所以j < i - 1。
            for (int j = 1; j < i - 1; j++) {
                dp[i] = Math.max(dp[i], Math.max(dp[i - j] * j, (i - j) * j));
            } 
        }
        return dp[n];
    }
}

96. 不同的二叉搜索树

class Solution {
    public int numTrees(int n) {
        //不用在意结点的值，只用在意有几个结点
        int dp[] = new int[n + 1];
        //空子树只存在一种情况，所以dp[0] = 1;
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            //以dp[3]为例 有三种情况，1、2、3分别为头结点
            //1为头结点，右子树dp[2]个结点，左子树dp[0]个结点，共dp[2] * dp[0]种情况
            //2为头，左右子树dp[1]，共dp[1] * dp[1]中情况
            //3为头，左子树dp[2]，右子树dp[0]，共dp[2] * dp[0]种情况
            for (int j = i; j >= 1; j--) {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
}

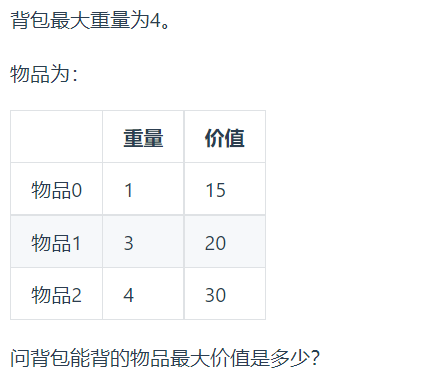
二维dp数组0/1背包

题目：

package LeetCode;

import java.util.Arrays;

public class zero_one_bag {
    public static void main(String[] args) {
        int[] weight = {1, 3, 4};
        int[] value = {15, 20, 30};
        int maxWeight = 4;
        testZeroOneBag01(weight, value, maxWeight);
    }

    private static void testZeroOneBag01(int[] weight, int[] value, int maxWeight) {
        int n = weight.length;
        int[][] dp = new int[n + 1][maxWeight + 1];
        //初始化 j < weight[0]时可装价值0
        for (int j = weight[0]; j <= maxWeight; j++) {
            dp[0][j] = value[0];
        }
        for (int i = 1; i < n; i++) {
            for (int j = 0; j <= maxWeight; j++) {
                //递推式 1、当背包容重小于当前物品i重量时，等于i-1的以容重j为条件的总价值
                //2、大于当前物品i重量，max(d[i - 1][j], dp[i - 1][j - weight[i]])
                if (j < weight[i]) dp[i][j] = dp[i - 1][j];
                else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
            }
        }
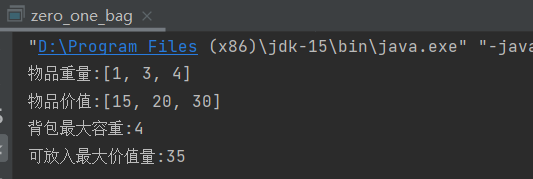
        System.out.println("物品重量:" + Arrays.toString(weight));
        System.out.println("物品价值:" + Arrays.toString(value));
        System.out.println("背包最大容重:" + maxWeight);
        System.out.println("可放入最大价值量:" + dp[n - 1][maxWeight]);
    }
}

参考：programmercarl.com