考试总结
DP 专题考试
这几天考了很多场 DP 啊,属实是考废了,中途因为唐氏错误保龄了一次,其他几次考的也不是很理想,可能跟最近低迷的状态有关吧。
现在开学停课搞竞赛,先把前几天的 DP 总结一下。
Day1(2024.8.30)
T1 天平(balance)
题意
有一个杠杆,有若干个秤砣,重量为 \(w_i\),和若干个可以放置秤砣的位置 \(p_i\),求 在使用所有秤砣的条件下,有多少种挂秤砣的方案,可以使杠杆平衡(力矩之和为 0)。
思路
我们考虑 \(dp_{i,j}\) 表示的是放了前 \(i\) 个秤砣,当前力矩为 \(j\) 的方案数。
对于当前秤砣 \(i\),它放到第 \(j\) 个可以放的位置的力矩为 \(w_i \times p_j\)。
那么就能得到:
再看一眼限制:
\(n,m \le 20\)
直接秒了(为什么时间如此充裕)。
代码
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define PII pair<int,int>
#define mk(a,b) make_pair(a,b)
using namespace std;
template<typename P>
inline void read(P &x){
P res=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
res=(res<<3)+(res<<1)+(ch^48);
ch=getchar();
}
x=res*f;
}
template<typename PP>
inline void write(PP x){
if(x<0) putchar('-'),x=-x;
if(x>=10) write(x/10);
putchar('0'+x%10);
}
int T=1;
int n,m;
int w[22],s[22],co[22][22];
unordered_map<int,int> dp[22];//前 i 个力举之和为 j
signed main(){
auto solve=[&](){
read(n),read(m);
for(int i=1;i<=n;++i) read(s[i]);
for(int i=1;i<=m;++i) read(w[i]);
for(int i=1;i<=m;++i){
for(int j=1;j<=n;++j){
co[i][j]=s[j]*w[i];
}
}
dp[0][0]=1;
for(int i=1;i<=m;++i){
for(int j=-10000;j<=10000;++j){
for(int k=1;k<=n;++k){
dp[i][j]=dp[i-1][j-co[i][k]]+dp[i][j];
}
}
}
cout<<dp[m][0]<<endl;
};
freopen("balance.in","r",stdin);
freopen("balance.out","w",stdout);
// read(T);
while(T--) solve();
return 0;
}
T2 山峰数(hill)
题意
山峰数是指数字排列中不存在山谷(先降后升)的数,例如 0,5,13,12321 都是山峰数,101,1110000111 都不是山峰数。
现给出 n 个数,请依次判断它们是否为山峰数,如果不是,输出-1。如果是,求出比它小的数中有多少个山峰数。
思路
简单数位 DP,因为要考虑之前是否下降过,所以在转移过程过添加一维 \(flag\) 表示之前是否已经下降过了,然后还需要一维前缀 \(pre\)。
填数字的时候只需要判断一下是否 \(flag\) 并且当前填的数比前缀 \(pre\) 大,如果是,则跳过,否则搜索。
如果当前是下降的,把 \(flag\) 设为 \(1\) 即可,其余情况不变。
其实数位 DP 用记忆化搜索好理解多了。
代码
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define PII pair<int,int>
#define mk(a,b) make_pair(a,b)
using namespace std;
template<typename P>
inline void read(P &x){
P res=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
res=(res<<3)+(res<<1)+(ch^48);
ch=getchar();
}
x=res*f;
}
template<typename PP>
inline void write(PP x){
if(x<0) putchar('-'),x=-x;
if(x>=10) write(x/10);
putchar('0'+x%10);
}
int T=1;
char a[72];
int n;
int num[72];
int f[72][72][2];
int dfs(int now,bool op0,bool lim,int pre,bool flag){
if(!now) return 1;
if(!op0 && !lim && f[now][pre][flag]!=-1) return f[now][pre][flag];
int up=lim?num[now]:9,res=0;
for(int i=0;i<=up;++i){
if(flag && i<=pre) res+=dfs(now-1,(op0 && i==0),(lim && i==up),i,1);
else if(!flag) res+=dfs(now-1,(op0 && i==0),(lim && i==up),i,(i<pre));
}
if(!op0 && !lim) f[now][pre][flag]=res;
return res;
}
signed main(){
memset(f,-1,sizeof(f));
auto solve=[&](){
cin>>(a+1);
n=strlen(a+1);
bool down=0;
for(int i=1;i<=n;++i) num[i]=a[i]-'0';
for(int i=1;i<n;++i){
if(num[i]<num[i+1] && down){
cout<<-1<<endl;
return;
}
if(num[i]>num[i+1]) down=1;
}
reverse(num+1,num+n+1);
cout<<dfs(n,1,1,0,0)-1<<endl;
};
freopen("hill.in","r",stdin);
freopen("hill.out","w",stdout);
read(T);
while(T--) solve();
return 0;
}
T3 粉刷匠 2(draw)
题意
\(4 \times n\) 的矩阵,有 256 种颜色,每个位置都可以选择一种颜色。
现在要满足以下条件:
- \(A(x,y) \ge A(x,y-1)\)
- 有一些指定的 \((x1,y1)\) 和 \((x2,y2)\),要求 \(A(x1,y1)=A(x2,y2)\)
求方案数,只输出答案后 5 位。
思路
比较有意思的背包。
我们不按照常规思维枚举行列,而是从小到大枚举颜色。若当前枚举到的颜色为 \(i\),我们使用 \(dp[l1][l2][l3][l4]\) 表示每一行使用当前颜色涂到哪一个位置。
假设有一行现在是 123344556,现在涂 7,显然涂 7 只能涂序列的后缀,比如涂成 123777777,或者 123344577 才能符合条件。所以考虑枚举当前颜色涂到哪个后缀来转移,转移时同样需要使用完全背包的降维思想优化。
对于限制条件,我们需要把不符合限制条件的去掉,什么样的方案符合限制条件呢?对于限制条件 \(A(x1,y1) = A(x2,y2)\),和当前枚举到的颜色 \(i\),要么 \(x1\) 行和 \(x2\) 行,当前颜色都涂到了 \(y1,y2\) 位置,要么都没有涂到 \(y1,\) 位置。除此之外的都是不合法的方案,我们事先处理好一个 \(vis\) 数组,\(vis[l1][l2][l3][l4]\) 表示四行分别涂到 \(l1,l2,l3,l4\),是否可行,在 dp 时如果遇到标记不可行的 \(vis\),这 dp 值设为 \(0\) 即可。
代码
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define PII pair<int,int>
#define mk(a,b) make_pair(a,b)
using namespace std;
template<typename P>
inline void read(P &x){
P res=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
res=(res<<3)+(res<<1)+(ch^48);
ch=getchar();
}
x=res*f;
}
template<typename PP>
inline void write(PP x){
if(x<0) putchar('-'),x=-x;
if(x>=10) write(x/10);
putchar('0'+x%10);
}
int T=1;
const int mod=100000;
int n,m,tc=1;
int c[4];
int f[16][16][16][16];
bool vis[16][16][16][16];
int r1x[105],r2x[105],r1y[105],r2y[105];
signed main(){
auto solve=[&](){
for(int tt=1;tt<=tc;++tt){
memset(vis,0,sizeof(vis));
read(n),read(m);
for(int i=1;i<=m;++i){
read(r1x[i]),read(r1y[i]),read(r2x[i]),read(r2y[i]);
r1x[i]--,r2x[i]--;
}
for(int i=1;i<=m;++i){
for(c[0]=0;c[0]<=n;++c[0])
for(c[1]=0;c[1]<=n;++c[1])
for(c[2]=0;c[2]<=n;++c[2])
for(c[3]=0;c[3]<=n;++c[3])
if(c[r1x[i]]>=r1y[i]^c[r2x[i]]>=r2y[i])
vis[c[0]][c[1]][c[2]][c[3]]=1;
}
memset(f,0,sizeof(f));
f[0][0][0][0]=1;
for(int col=0;col<=255;++col){
for(int cc=0;cc<=3;++cc)
for(c[0]=0;c[0]<=n;++c[0])
for(c[1]=0;c[1]<=n;++c[1])
for(c[2]=0;c[2]<=n;++c[2])
for(c[3]=0;c[3]<=n;++c[3])
if(c[cc]<n){
int tmp=f[c[0]][c[1]][c[2]][c[3]];
c[cc]++;
f[c[0]][c[1]][c[2]][c[3]]=(f[c[0]][c[1]][c[2]][c[3]]+tmp)%mod;
c[cc]--;
}
for(c[0]=0;c[0]<=n;++c[0])
for(c[1]=0;c[1]<=n;++c[1])
for(c[2]=0;c[2]<=n;++c[2])
for(c[3]=0;c[3]<=n;++c[3])
if(vis[c[0]][c[1]][c[2]][c[3]]) f[c[0]][c[1]][c[2]][c[3]]=0;
}
printf("%05d\n",f[n][n][n][n]);
}
};
// freopen("draw.in", "r", stdin);
// freopen("draw.out", "w", stdout);
//read(T);
while(T--) solve();
return 0;
}
T4 棋盘(knight)
题意
有一个 \(N \times M\) 的棋盘,要在上面摆上 knight,每个格子可以放至多一个 knight。
knight 的攻击范围为国际象棋中马的移动范围。
所有 knight 不能互相攻击,请问总共有多少可行的摆法?答案对 1000000007 取模。
思路
状压 DP
考虑压当前行,上一行,上两行三个状态。
转移还是正常转移,但是这样你会发现你寄了。
这个时候我们发现可以使用矩阵优化。
咕咕咕
模拟考
NOIP 联测(2024.10.23)
T1 tree
题意

思路
构造题,如果注意力十分集中,能够注意到,菊花图带链(蒲公英)是近似于正确的答案,但发现取中间时会错,那可以构造两条链,即两条链的菊花图即可
代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
template<typename P>
void read(P &x){
P res=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
res=(res<<3)+(res<<1)+ch-'0';
ch=getchar();
}
x=res*f;
}
int T=1;
int tp,n,x;
void solve(){
cin>>tp>>n>>x;
if((x<2 || x>n/2+1) && (n!=1 || x!=1)){
cout<<"No"<<'\n';
return;
}
else cout<<"Yes"<<'\n';
if(tp==0 || n==1) return;
int t=n/2+1,tt=t-x+1;
for(int i=1;i<=tt;++i) cout<<i<<' '<<tt+1<<'\n';
for(int i=tt+1;i<n;++i) cout<<i<<' '<<i+1<<'\n';
return;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
freopen("tree.in","r",stdin);
freopen("tree.out","w",stdout);
cin>>T;
while(T--) solve();
return 0;
}
T2 suffix
题意

思路
我们发现一个满足条件的区间,最后一个必定与整个字符串最后一个相同,即
这样我们只需要考虑以 \(S_n\) 结尾的区间 \([l,r]\),然后发现我们可以先求最长公共后缀能抵达的位置,记为 \(f_i\),这个的意义就是求与后缀的 \(boader\) 的反序。

图中的每个箭头的终点表示的是初始时 \(f[r]\) 的的值,我们发现这个箭头具有传递性,意思是如果 \(f[i]>f[i-1]\) 那么这个区间必定可以分成 \([f_{i-1},i-1]\) 和 \([i-1,i]\),然后这个东西相当于在 \([f_i,i]\) 求最小值,可以用线段树处理,至于前面的预先求出最长 \(border\),可以用二分 Hash 或者倍增,exKMP 都可以处理。
简洁一点:
- 求当前位置的最长后缀能达到的位置 \(F_i\)
- 对 \([F_i,i]\) 求 \(F_i\) 最小值(传递性),这就是以 \(i\) 结尾的最长的能被分成若干个后缀的区间的左端点位置。
- 那么询问就是判断是否 \(F_r<=l\) 即可。
代码
#include<bits/stdc++.h>
#define endl "\n"
#define int long long
using namespace std;
template<typename P>
void read(P &x){
P res=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(isdigit(ch)){
res=(res<<3)+(res<<1)+ch-'0';
ch=getchar();
}
x=res*f;
}
int T=1;
const int N=1e6+10,mod=1e9+7,base=1e6+7;
const int INF=0x3f3f3f3f3f3f3f3f;
int n,q;
char s[N];
int nxt[N],f[N];
int h[N],be[N];
int query(int l,int r){
return (h[r]-h[l-1]*be[r-l+1]%mod+mod)%mod;
}
struct Stree{
#define lson (rt<<1)
#define rson (rt<<1|1)
int t[N<<2];
void pushup(int rt){
t[rt]=min(t[lson],t[rson]);
}
void build(int rt,int l,int r){
if(l==r) {t[rt]=INF;return;}
int mid=(l+r)>>1;
build(lson,l,mid);
build(rson,mid+1,r);
pushup(rt);
}
void update(int rt,int l,int r,int k,int x){
if(l==r) {t[rt]=x;return;}
int mid=(l+r)>>1;
if(k<=mid) update(lson,l,mid,k,x);
else update(rson,mid+1,r,k,x);
pushup(rt);
}
int query(int rt,int l,int r,int L,int R){
if(L<=l && r<=R) return t[rt];
int mid=(l+r)>>1,res=INF;
if(L<=mid) res=min(res,query(lson,l,mid,L,R));
if(R>mid) res=min(res,query(rson,mid+1,r,L,R));
return res;
}
}Q;
signed main(){
auto solve=[&](){
read(n),read(q);
scanf("%s",s+1);
be[0]=1;
for(int i=1;i<=n;++i){
h[i]=(h[i-1]*base%mod+(s[i]-'a'+1))%mod;
be[i]=be[i-1]*base%mod;
}
Q.build(1,1,n);
char op=s[n];
memset(f,0x3f,sizeof(f));
for(int i=1;i<=n;++i){
if(s[i]==op){
int l=1,r=i,ans=0;
while(l<=r){
int mid=(l+r)>>1;
if(query(i-mid+1,i)==query(n-mid+1,n)) l=mid+1,ans=mid;
else r=mid-1;
}
f[i]=i-ans+1;
Q.update(1,1,n,i,f[i]);
f[i]=Q.query(1,1,n,max(f[i]-1,1ll),i);
Q.update(1,1,n,i,f[i]);
}
}
while(q--){
int l,r;
read(l),read(r);
int id=f[r];
if(id<=l) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
return;
};
freopen("suffix.in","r",stdin);
freopen("suffix.out","w",stdout);
// read(T);
while(T--) solve();
return 0;
}
T3 subsequence
题意

思路
发现对于第二个性质,我们 \(ln\) 一下发现有 \(b \ln a < a \ln b\),即 \(\dfrac{a}{\ln a}>\dfrac{b}{\ln b}\)。
考虑函数 \(f(x)=\dfrac{x}{\ln x}\),求导有 \(f'(x)=\ln(x)^{-1}-\ln(x)^{-2}\)。不难看出 \(f'(x)\) 有唯一零点 \((e,0)\),故 \(f(x)\) 在 \(x=e\) 时取得最小值。
所以在 \(i<j\) 且 \(i>e\) 时,总有 \(b_{i}^{b_{j}} < b_{j}^{b_{i}}\)。
其实看不懂没关系,只需要打表观察发现序列 \(B\) 的种类其实很少,分下面 3 类:
-
序列无 \(1\):则顺序对至多为 \(1\),无合法序列。
-
序列有 \(1\),不同时存在 \(2,3\):此时记序列长度为 \(n\),则顺序对数为 \(n-1\),逆序对数为 \(\dfrac{(n-1)(n-2)}{2}\)。联立解得 \(n=4\),故此时子序列呈 \(\{1 , a, b, c\}(a>b>c)\)。
-
序列有 \(1\),同时存在 \(2,3\),同理解方程,可知此时子序列呈 \(\{1 , a, b, 2, 3\}(a>b \ne 4)\)。
所以序列的最大长度暂且为 \(4\),第三种情况我们先不管。那么有贡献的必定为 \(B_2,B_3\),那么我们可以开两个值域线段树存的是 \(B_2,B_3\) 的数量。
每次碰到一个不是 \(2\) 的,那么将它加进第一颗线段树,统计线段树内它后面的元素个数总和,将这个总和加进第二颗线段树,再对第二颗线段树内它后面的元素个数求和累加进 \(ans\)。如果碰到 \(2\),\(ans\) 还是要累加答案的,但同时累加到 \(ans2\) 中,因为如果 \(B\) 序列是 \(\{1,9,8,2,3\}\),那么还是有贡献的,单独处理一下即可。
代码
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define PII pair<int,int>
#define mk(a,b) make_pair(a,b)
using namespace std;
template<typename P>
inline void read(P &x){
P res=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
res=(res<<3)+(res<<1)+(ch^48);
ch=getchar();
}
x=res*f;
}
template<typename PP>
inline void write(PP x){
if(x<0) putchar('-'),x=-x;
if(x>=10) write(x/10);
putchar('0'+x%10);
}
int T=1;
const int N=1e6+10,mod=998244353;
int n;
int a[N];
struct Stree{
#define lson (rt<<1)
#define rson (rt<<1|1)
int t[N<<2];
void pushup(int rt) {t[rt]=t[lson]+t[rson];t[rt]%=mod;}
void update(int rt,int l,int r,int k,int x){
if(l==r) {t[rt]+=x,t[rt]%=mod;return;}
int mid=(l+r)>>1;
if(k<=mid) update(lson,l,mid,k,x);
else update(rson,mid+1,r,k,x);
pushup(rt);
}
int query(int rt,int l,int r,int L,int R){
if(L<=l && r<=R) return t[rt];
int mid=(l+r)>>1,res=0;
if(L<=mid) res+=query(lson,l,mid,L,R),res%=mod;
if(R>mid) res+=query(rson,mid+1,r,L,R),res%=mod;
return res%mod;
}
}Q1,Q2;
signed main(){
auto solve=[&](){
read(n);
for(int i=1;i<=n;++i) read(a[i]);
int f1=0;
int ans=0,ans2=0;
for(int i=1;i<=n;++i){
if(a[i]==1) {f1++;continue;}
if(f1==0) continue;
Q1.update(1,1,n,a[i],f1);
int tot=Q1.query(1,1,n,a[i]+1,n);
Q2.update(1,1,n,a[i],tot);
if(a[i]==2) ans+=Q2.query(1,1,n,5,n),ans2+=Q2.query(1,1,n,5,n),ans%=mod,ans2%=mod;
else ans+=Q2.query(1,1,n,a[i]+1,n),ans%=mod;
if(a[i]==3) ans+=ans2,ans%=mod;
}
cout<<(ans+n)%mod<<endl;
};
freopen("subsequence.in","r",stdin);
freopen("subsequence.out","w",stdout);
//read(T);
while(T--) solve();
return 0;
}
CSP-S(2024.10.24)
T1 queue
题意

思路
太唐了,直接写。
代码
#include<bits/stdc++.h>
#define endl "\n"
#define ll long long
using namespace std;
template<typename P>
void read(P &x){
P res=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-') f=-1;
ch=getchar();
}
while(isdigit(ch)){
res=(res<<3)+(res<<1)+ch-'0';
ch=getchar();
}
x=f*res;
}
int T=1;
int n;
void solve(){
read(n);
if(n%2==0){
for(int i=n;i>=1;i-=2) printf("%d ",i);
for(int i=1;i<=n;i+=2) printf("%d ",i);
}
else{
for(int i=n;i>=1;i-=2) printf("%d ",i);
for(int i=2;i<=n;i+=2) printf("%d ",i);
}
puts("");
return;
}
signed main(){
freopen("queue.in","r",stdin);
freopen("queue.out","w",stdout);
// read(T);
while(T--) solve();
return 0;
}
T2 cutin
题意

思路
本来是想做 DP 的,但是发现一些性质:
- 对于 \([m+1,n]\) 的队伍,无论怎么走反正都是要走完的,然后我们可以发现,在某个位置停下相当于选了这个位置的 \(a_i\),如果不停下就是选了 \(b_i\),那么这一段相当于就是选 \(a_i\) 和 \(b_i\) 的较小值即可。
- 对于 \([1,m]\) 的队伍,最多只会停一次(因为已经满足要求了就不用走了),我们考虑在哪儿停下,发现在 \(i\) 停下的花费是 \(a_i+\sum\limits_{j=i}^{m}b_j\),后面的求和用前缀和处理即可,求一个最小值就行。
PS:其实 DP 也能做。
代码
#include<bits/stdc++.h>
#define endl "\n"
#define int long long
using namespace std;
template<typename P>
void read(P &x){
P res=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-') f=-1;
ch=getchar();
}
while(isdigit(ch)){
res=(res<<3)+(res<<1)+ch-'0';
ch=getchar();
}
x=f*res;
}
int T=1;
const int N=2e5+10;
int n,m;
int a[N],b[N];
int sumb[N],sum[N];
void solve(){
read(n),read(m);
for(int i=1;i<=n;++i) read(a[i]);
for(int i=1;i<=n;++i) read(b[i]),sumb[i]=sumb[i-1]+b[i];
int ans=0;
for(int i=n;i>m;--i){
if(a[i]>b[i]) ans+=b[i];
else ans+=a[i];
}
int sum=0x3f3f3f3f;
for(int i=1;i<=m;++i){
sum=min(sum,a[i]+sumb[m]-sumb[i]);
}
printf("%lld\n",ans+sum);
return;
}
signed main(){
freopen("cutin.in","r",stdin);
freopen("cutin.out","w",stdout);
read(T);
while(T--) solve();
return 0;
}
T3 number
题意

思路
一眼数位 DP,但是写完后发现需要存每个数字,\(1e18\) 的数据根本不行,我们换一种方法。
我们发现一个数取模 \(2520\)(\([1,9]\) 所有数字的 \(\operatorname {lcm}\))后再考虑也是等价的,即
那么现在就可以从 \(1e18\) 压缩到 \(2520\) 了,剩下的还需要存一下现在选的数字的 \(\gcd\),以及 \(\operatorname {lcm}\)(这二者可以使用状压维护每个数字)最后就是正常数位 DP 了。
代码
#include<bits/stdc++.h>
#define endl "\n"
#define int long long
using namespace std;
template<typename P>
void read(P &x){
P res=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-') f=-1;
ch=getchar();
}
while(isdigit(ch)){
res=(res<<3)+(res<<1)+ch-'0';
ch=getchar();
}
x=f*res;
}
int T=1;
int num[20];
int Gcd[3005];
int to=0;
int f[20][2601][51];
int gcd(int a,int b){
if(!b) return a;
return gcd(b,a%b);
}
int lc(int x,int y){
return x*y/gcd(x,y);
}
int dfs(int now,int op0,int lim,int sum,int yu){
if(!now) return (yu%sum==0);
if(!lim && !op0 && f[now][yu][Gcd[sum]]!=-1) return f[now][yu][Gcd[sum]];
int up=(lim)?num[now]:9,res=0;
for(int i=0;i<=up;++i){
if(i==0 && op0!=1) continue;
res+=dfs(now-1,(op0 && i==0),(lim && i==up),(i?lc(sum,i):sum),(yu*10+i)%2520);
}
if(!lim && !op0) f[now][yu][Gcd[sum]]=res;
return res;
}
int work(int x){
int len=0;
memset(f,-1,sizeof(f));
while(x){
num[++len]=x%10;
x/=10;
}
return dfs(len,1,1,1,0);
}
void solve(){
int l,r;
read(l),read(r);
for(int i=1;i<=2520;++i){
if(!(2520%i)) Gcd[i]=(++to);
}
cout<<work(r)-work(l-1)<<endl;
return;
}
signed main(){
freopen("number.in","r",stdin);
freopen("number.out","w",stdout);
// read(T);
while(T--) solve();
return 0;
}
NOIP 联测(2024.11.20)
T1 a
题意
P9827 [ICPC2020 Shanghai R] Sky Garden

思路
大致意思就是求若干个圆心为 \((0,0)\) 的同心圆与若干条过圆心的直线的交点之间的最短路之和。
发现可以分开讨论走圆弧和走直线的路径。
由于圆弧是等分的,所以一个点要走圆弧的相邻路径可以容易得出,剩下的就是算某个点到其他点走直线所花的的距离。
luogu 上的复杂度可以 \(O(N^3)\),赛时是加强版,只能 \(O(N)\) 及以下,乱搞一下就 ok 了。
代码
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
#define ull unsigned long long
#define PII pair<int,int>
#define mk(a,b) make_pair(a,b)
using namespace std;
template<typename P>
inline void read(P &x){
P res=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
res=(res<<3)+(res<<1)+(ch^48);
ch=getchar();
}
x=res*f;
}
template<typename Ty,typename ...Args>
inline void read(Ty &x,Args &...args) {read(x);read(args...);}
int T=1;
const int mod=998244353;
const double pi=acos(-1);
int n,m;
inline void solve(){
read(n,m);
int cnt=0,ans1=0,ans2=0;
for(int i=1;i<=m;++i) if(1.0*pi/m*i>2.0) {cnt=i-1;break;}
int num=(cnt+1)*cnt/2%mod;
for(int i=1;i<=n;++i){
ans1+=i*num%mod*2%mod+(n-i)*2%mod*num%mod*i%mod*2%mod;
ans1%=mod;
}
for(int i=1;i<=n;++i){
ans2=(ans2+(n-i+1)*(n-i)%mod*m%mod+2*m%mod*i%mod+(n-i+1)*(n-i)%mod*cnt%mod*m%mod*2%mod)%mod;
int p=((n+1)*n/2%mod+n*i%mod)%mod;
ans2=(ans2+p*((m-cnt)*2-1)%mod*m%mod)%mod;
}
cout<<(ans1+mod+mod)%mod<<' '<<(ans2+mod+mod)%mod<<endl;
}
signed main(){
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
//read(T);
while(T--) solve();
return 0;
}
剩下的不会。咕咕咕。
NOIP 联测(2024.11.25)
T1 chtholly
题意

思路
一开始想到缩点,但是发现缩完点后就不能求 LCA,非常复杂。然后因为是长度为 3 的简单环,可以考虑构建圆方树,只有 2 个点的要么不建方点,要么建了方点不标记成有贡献的。
那么现在对于一次询问 \((u,v,k)\),算出二者间的距离 \(dis\),然后有 2 种情况:
- \(k<dis\),无解,输出 0
- \(k\ge dis\),此时意味着我们需要选择一些更长的路径。发现走一次方点相当于使总路程 \(+1\),算出差值 \(cz\) 与路径上的方点数 \(sum\),那么答案就是 \(sum \choose cz\)。
代码
#include<bits/stdc++.h>
#define endl '\n'
#define ll long long
#define ull unsigned long long
#define PII pair<int,int>
#define mk(a,b) make_pair(a,b)
using namespace std;
template<typename P>
inline void read(P &x){
P res=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
res=(res<<3)+(res<<1)+(ch^48);
ch=getchar();
}
x=res*f;
}
template<typename Ty,typename ...Args>
inline void read(Ty &x,Args &...args) {read(x);read(args...);}
int T=1;
const int N=2e5+10,mod=998244353,M=4e5+40;
int n,m,q,id,cnt;
vector<int> g[N],ge[M];
int yu[M];
bool flag[M];
ll fac[M];
int st[N],tpp,low[N],dfx[N],tot;
int son[M],siz[M],tp[M],f[M],dep[M];
void add(int u,int v){
ge[u].push_back(v);
ge[v].push_back(u);
}
void tanjan(int u,int fa){
low[u]=dfx[u]=++tot;
st[++tpp]=u;
int son=0;
for(auto to:g[u]){
if(!dfx[to]){
son++;
tanjan(to,u);
low[u]=min(low[u],low[to]);
if(low[to]>=dfx[u]){
++cnt;
int jg=0;
while(st[tpp+1]!=to){
add(st[tpp--],cnt);
jg++;
}
add(u,cnt);
if(jg!=1) flag[cnt]=1;
}
}
else low[u]=min(low[u],dfx[to]);
}
if(fa==0 && son==0) add(u,cnt);
}
void dfs1(int u,int fa){
siz[u]=1;
f[u]=fa;
dep[u]=dep[fa]+1;
yu[u]=yu[fa]+flag[u];
for(auto to:ge[u]){
if(to==fa) continue;
dfs1(to,u);
siz[u]+=siz[to];
if(siz[to]>siz[son[u]]) son[u]=to;
}
}
void dfs2(int u,int t){
tp[u]=t;
if(son[u]) dfs2(son[u],t);
for(auto to:ge[u]){
if(to==f[u] || to==son[u]) continue;
dfs2(to,to);
}
}
int lca(int a,int b){
while(tp[a]!=tp[b]){
if(dep[tp[a]]<dep[tp[b]]) swap(a,b);
a=f[tp[a]];
}
if(dep[a]<dep[b]) swap(a,b);
return b;
}
ll qpow(ll a,ll b){
ll res=1;
while(b){
if(b&1) res=a*res%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
ll inv(int a){
return qpow(a,mod-2)%mod;
}
ll bal(int n,int m){
return fac[n]*inv(fac[m])%mod*inv(fac[n-m])%mod;
}
inline void solve(){
read(id,n,m,q);
fac[0]=1;
for(int i=1;i<=n*2;++i) fac[i]=fac[i-1]*i%mod;
for(int i=1;i<=m;++i){
int u,v;
read(u,v);
g[u].push_back(v);
g[v].push_back(u);
}
cnt=n;
tanjan(1,0);
dfs1(1,1);
dfs2(1,0);
for(int i=1;i<=q;++i){
int u,v,k;
read(u,v,k);
ll lcc=lca(u,v);
ll di,you;
di=(dep[u]+dep[v]-2*dep[lcc])/2,you=yu[u]+yu[v]-2*yu[lcc]+flag[lcc];
if(di>k) cout<<0<<endl;
else cout<<bal(you,k-di)%mod<<endl;
}
}
signed main(){
freopen("chtholly.in","r",stdin);
freopen("chtholly.out","w",stdout);
//read(T);
while(T--) solve();
return 0;
}
T2 hoshino
题意

思路
一个明显的性质:优先放数量最多的物资。
发现每次移动区间最多会使物质次数 \(-1\),考虑莫队,需要用一个桶存一下每一种物资的人数。还需要一个二号桶存一下有多少种物资的人数为 \(x\)。那么移动区间时更新一下桶。
统计答案时从人数最多的二号桶从大到小枚举
容易发现:
细节可以想一下。
代码
#include<bits/stdc++.h>
#define endl '\n'
#define ll long long
#define ull unsigned long long
#define PII pair<int,int>
#define mk(a,b) make_pair(a,b)
using namespace std;
template<typename P>
inline void read(P &x){
P res=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
res=(res<<3)+(res<<1)+(ch^48);
ch=getchar();
}
x=res*f;
}
template<typename Ty,typename ...Args>
inline void read(Ty &x,Args &...args) {read(x);read(args...);}
int T=1;
const int N=3e5+10;
int n,m,idd,siz;
int id[N];
struct node{
int x,id;
bool operator < (const node &a)const{
return x<a.x;
}
}a[N];
int b[N];
ll Ans[N];
struct que{
int l,r,id;
}q[N];
int p[N],tp[N],mx=-0x3f3f3f3f;
bool cmp(que a,que b){
return (id[a.l]==id[b.l])?a.r<b.r:a.l<b.l;
}
void add(int x){
tp[p[x]]--;
p[x]++;
tp[p[x]]++;
mx=max(mx,p[x]);
}
void del(int x){
if(p[x]!=0) tp[p[x]]--;
p[x]--;
tp[p[x]]++;
mx=max(mx,p[x]);
}
inline void solve(){
read(idd,n,m);
siz=sqrt(n);
for(int i=1;i<=n;++i) id[i]=(i-1)/siz+1;
for(int i=1;i<=n;++i) read(a[i].x),a[i].id=i,b[i]=a[i].x;
for(int i=1;i<=m;++i){
int l,r;
read(l,r);
q[i].l=l,q[i].r=r;
q[i].id=i;
}
sort(a+1,a+n+1);
sort(q+1,q+m+1,cmp);
int cnt=0;
for(int i=1;i<=n;i++){
if(a[i].x!=a[i-1].x) cnt++;
b[a[i].id]=cnt;
}
for(int i=1;i<=n;i++) a[i].x=b[i];
int l=1,r=0;
ll ans=0;
for(int i=1;i<=m;++i){
int ql=q[i].l,qr=q[i].r;
while(r<qr) add(a[++r].x);
while(l>ql) add(a[--l].x);
while(l<ql) del(a[l++].x);
while(r>qr) del(a[r--].x);
ll res=0;
ans=0;
for(int j=mx;j>=1;--j){
if(!tp[j]) continue;
ans+=(tp[j]*res+(tp[j]-1)*tp[j]/2)*j;
res+=tp[j];
}
Ans[q[i].id]=ans;
}
for(int i=1;i<=m;++i) cout<<Ans[i]<<endl;
}
signed main(){
freopen("hoshino.in","r",stdin);
freopen("hoshino.out","w",stdout);
//read(T);
while(T--) solve();
return 0;
}
NOIP 联测(2024.11.26)
T1 for ya
题意

思路
好题!
我们发现 \(\frac{2}{3} n\) 这个条件很奇怪,似乎没什么用处,但是其实我们有一个性质:
若两个点之间无边,则不可能同时出现在答案中
所以我们考虑每次遍历两个点,若这两个点之间无边,则删掉这两个点。最后一定能找到 \(\frac{1}{3}n\) 个点构成完全图
考虑证明正确性:假设我们找到的无边的点最坏情况下都是一个在 \(\frac{2}{3}n\) 的完全块中,一个不在,那么每次删点最多会删掉一个本来就在完全图中的点。
加之最多存在 \(\frac{1}{3}n\) 两两之间都不构成完全图(最坏情况),所以最多删去 \(\frac{2}{3}n\) 个点,那么剩余的 \(\frac{1}{3}n\) 个点必定都是完全块中剩下的,故一定两两联通。
代码
#include<bits/stdc++.h>
#define endl '\n'
#define ll long long
#define ull unsigned long long
#define PII pair<int,int>
#define mk(a,b) make_pair(a,b)
using namespace std;
template<typename P>
inline void read(P &x){
P res=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
res=(res<<3)+(res<<1)+(ch^48);
ch=getchar();
}
x=res*f;
}
template<typename Ty,typename ...Args>
inline void read(Ty &x,Args &...args) {read(x);read(args...);}
int T=1;
const int N=3030;
int n,m;
bool a[N][N];
bool vis[N];
inline void solve(){
read(n,m);
for(int i=1;i<=m;++i){
int u,v;
read(u,v);
a[u][v]=a[v][u]=1;
}
for(int i=1;i<=n;++i){
for(int j=i+1;j<=n;++j){
if(!a[i][j] && !vis[i] && !vis[j]) vis[i]=vis[j]=1;
}
}
int sum=0;
for(int i=1;i<=n;++i) if(!vis[i]) sum++;
cout<<sum<<endl;
for(int i=1;i<=n;++i) if(!vis[i]) cout<<i<<' ';
cout<<endl;
}
signed main(){
freopen("ya.in","r",stdin);
freopen("ya.out","w",stdout);
//read(T);
while(T--) solve();
return 0;
}
T2 只因你太美
咕咕咕
T3 lagtrain
题意

思路
一个很显然的贪心:对于一个点 \(u\),将它所有子树的 \(size\) 分成两部分,要求这两部分差值尽量小,此时的乘积(即对答案的贡献)最大。
那么现在关键问题就是要将一个集合分成两个子集使得两个子集的差最小。
记集合的总和为 \(ss\),那么就是说我们要从一堆数中选一些尽量接近 \(ss\)。这个可以用 01 背包做,但是这样是 \(O(N^2)\) 的,对于 \(2e5\) 的数据是肯定过不去的。
考虑用 bitset 优化一下,这样 DP 的复杂度降到了 \(O(\frac{N^2}{\omega})\),但是统计答案时需要对整个 DP 数组遍历,复杂度又降为 \(O(N^2)\) 了,怎么办呢?
我们发现我们只需要知道 DP 数组(即 bitset)哪一位是 1 即代表这个位置是能凑出来的,所以只需要枚举 1 的位置。
这里有两个 bitset 的小函数:
a._Find_first()找到第一个 1 的位置a._Find_next(x)找到第 x 的位置后的第一个出现的 1 的位置(不含 x 本身)。
那么现在就可以通过这个函数去找 1 的位置。(其实我后面想了一下,好像只需要找到最靠近 \(\frac{sum}{2}\) 的 i 即可,不需要枚举)
for(int i=f._Find_next(ss/2-1);i!=f.size();i=f._Find_next(i)){res=max(res,1ll*i*(ss-i));}
这样就能在 \(O(\frac{N^2}{\omega})\) 的复杂度内 卡过 通过此题。
代码
#include<bits/stdc++.h>
#define endl '\n'
#define ll long long
#define ull unsigned long long
#define PII pair<int,int>
#define mk(a,b) make_pair(a,b)
using namespace std;
template<typename P>
inline void read(P &x){
P res=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
res=(res<<3)+(res<<1)+(ch^48);
ch=getchar();
}
x=res*f;
}
template<typename Ty,typename ...Args>
inline void read(Ty &x,Args &...args) {read(x);read(args...);}
int T=1;
const int N=2e5+10,M=5e3+10;
int n;
ll ans=0;
vector<int> g[N];
bitset<N> f;
static bitset<N> ff;
int siz[N];
int son[N];
void dfs(int u){
vector<int> s;
siz[u]=1;
ll ss=0,res=0;
for(auto to:g[u]){
dfs(to);
ss+=siz[to];
siz[u]+=siz[to];
s.push_back(siz[to]);
if(siz[son[u]]<siz[to]) son[u]=to;
}
if(siz[son[u]]>=siz[u]/2){ans+=siz[son[u]]*(ss-siz[son[u]]);return;}
f.reset();
f[0]=1;
for(int x:s) ff=f<<x,f|=ff;
for(int i=f._Find_next(ss/2-1);i!=f.size();i=f._Find_next(i)){res=max(res,1ll*i*(ss-i));}
ans+=res;
return;
}
inline void solve(){
read(n);
for(int i=2;i<=n;++i){
int x;
read(x);
g[x].push_back(i);
}
dfs(1);
cout<<ans<<endl;
}
signed main(){
freopen("train.in","r",stdin);
freopen("train.out","w",stdout);
//read(T);
while(T--) solve();
return 0;
}
NOIP 测试(2024.11.28)
T1 sub
题意

思路
考场上 5min 就搞定了,容易发现当 \(a,b\) 同号时答案必定为 0,因为可以辗转相减。
\(a,b\) 异号时容易得知要么不做任何操作,要么就只能做一次(因为再做的话差值会越来越大)。
然后做一次差值的答案时 \(|a-b+b|\) 和 \(|b-a+a|\)。
所以最后的答案就是 \(\min\{|a|,|b|,|a+b|\}\)。
代码
#include<bits/stdc++.h>
#define endl '\n'
#define ll long long
#define ull unsigned long long
#define PII pair<int,int>
#define mk(a,b) make_pair(a,b)
using namespace std;
template<typename P>
inline void read(P &x){
P res=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
res=(res<<3)+(res<<1)+(ch^48);
ch=getchar();
}
x=res*f;
}
template<typename Ty,typename ...Args>
inline void read(Ty &x,Args &...args) {read(x);read(args...);}
int T=1;
inline void solve(){
int a,b;
read(a,b);
if((a>=0 && b>=0) || (a<=0 && b<=0)) cout<<0<<endl;
else cout<<min(abs(a+b),min(abs(a),abs(b)))<<endl;
}
signed main(){
freopen("sub.in","r",stdin);
freopen("sub.out","w",stdout);
read(T);
while(T--) solve();
return 0;
}
T2 paint
题意

思路
考场上写的普通 DP,理论上能卡过 85pts 但是只有 40pts。
现在我们考虑其特殊性质(只有 2 种颜色),那么一次操作可以看成反转一个位置的颜色,则有:
- 最左边和最右边的格子是无法反转的。
- 相邻两个格子是无法同时反转的。

嗯大致就是这样,这个 \((\min,+)\) 矩阵就是说把矩阵魔改一下。

然后考虑多个颜色相同的格子可以缩成一个块是不影响正确性的。
现在考虑多个颜色。
一个性质:
- 当一个节点被染成不同的颜色后,一定存在最优解,该节点所在连通块不会去染其他颜色。
要是染一次又染还不如一次染完。
因此染色区间不交,考虑设置 dp 状态 \(f_{i,0}\)~\(_{m}\) 代表当前在第 \(i\) 个格子,并且该格子正在染色为 \(0\)~\(m\),\(0\) 代表当前没有操作。

使用 \(6 \times 6\) 的 \((\min,+)\) 矩阵加线段树可做。
代码咕咕咕。
北京冬季联训
Day 1(2024.12.16)
T1 背包问题(knapsack)
题意

思路
其实可以先考虑全部放在一号背包里,再挪动一些去其他背包。
转移到 2 号背包的贡献是 \(w_{i,1}-w_{i,2}\),3 号同理。
后问题转换为在 \(n\) 个二元组中选 \(y\) 个获得 \(e\) 收益,选 \(z\) 个获得 \(f\) 收益,最大化总收益。
考虑什么时候交换他们的选择收益不会变少,也就是 \(e_i+f_j \ge e_j + f_i\)。
移项得 \(e_i - e_j \ge f_i -f_j\)。所以按照这个排序。做一个堆。
就有对于任意 \(i<j\) ,如果 \(i\) 选 \(f\) 且 \(j\) 选 \(e\) ,那么交换两者状态一定不会变差。换言之,存在最优解满足选 \(e\) 的全在选 \(f\) 的左边,
也就是说存在一个 \(k\) 使得有最优解在 \(1\) 到 \(k\) 中取 \(y\) 个 \(e\) 在 \(k+1\) 到 \(n\) 中取 \(z\) 个 \(f\) 。
那么只需要通过优先队列预处理出每个前缀前 \(y\) 大的 \(e\) 的和以及每个后缀前 \(z\) 大的 \(f\) 的和。
话说居然还是道紫题。
代码
#include<bits/stdc++.h>
#define endl '\n'
#define ll long long
#define mk(a,b) make_pair(a,b)
#define PII pair<int,int>
using namespace std;
template<typename P>
void read(P &x){
P res=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-') f=-1;
ch=getchar();
}
while(isdigit(ch)){
res=(res<<3)+(res<<1)+(ch^48);
ch=getchar();
}
x=res*f;
}
template<typename PP,typename ...Arc>
void read(PP &x,Arc &...y) {read(x),read(y...);}
const int N=1e5+10;
struct node{
int a,b;
};
node p[N];
ll lsum[N],rsum[N];
signed main(){
int x,y,z;
read(x,y,z);
int n=x+y+z;
ll ans=0;
for(int i=1;i<=n;++i){
int a,b,c;
read(a,b,c);
ans+=a;
p[i].a=b-a,p[i].b=c-a;
}
sort(p+1,p+n+1,[](node x,node y){
return x.a-x.b>y.a-y.b;
});
priority_queue<int,vector<int>,greater<int> > q;
for(int i=1;i<=n;++i){
lsum[i]=lsum[i-1]+p[i].a;
q.push(p[i].a);
if(q.size()>y){
lsum[i]-=q.top();
q.pop();
}
}
while(!q.empty()) q.pop();
for(int i=n;i>=1;--i){
rsum[i]=rsum[i+1]+p[i].b;
q.push(p[i].b);
if(q.size()>z){
rsum[i]-=q.top();
q.pop();
}
}
ll maxx=-0x3f3f3f3f3f3f3f3f;
for(int i=y;i<=n-z;++i) maxx=max(maxx,lsum[i]+rsum[i+1]);
cout<<ans+maxx<<endl;
return 0;
}
剩下两道不会了咕咕咕。
Day 2(2024-12-17)
T1 石子游戏(stone)
题意

思路
博弈论,考场上写出来了,考虑首先大于 3 的数等价于 3。至于为什么不是 2,因为 B 可以连拿两次,所以如果是 2 的话意味着必定拿完,而 3 就可以剩 1 个。
然后分讨一下,如果只有 1,那么输赢只和 1 的个数与 3 的模数有关。
如果有 1 有 2,则:
-
如果有 1 个 2,则必胜。
-
如果有 2 个 2 且 1 的个数不是 3 的倍数,则必胜
-
其余必输。
如果都有,容易发现当 3 的个数大于 1 之后必输。所以只考虑等于 1 的情况。
同样根据 1 和 2 的个数分讨一下,这里不再赘述。
代码
#include<bits/stdc++.h>
#define endl '\n'
#define ll long long
#define mk(a,b) make_pair(a,b)
#define PII pair<int,int>
using namespace std;
template<typename P>
void read(P &x){
P res=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-') f=-1;
ch=getchar();
}
while(isdigit(ch)){
res=(res<<3)+(res<<1)+(ch^48);
ch=getchar();
}
x=res*f;
}
template<typename PP,typename ...Arc>
void read(PP &x,Arc &...y) {read(x),read(y...);}
int T=1;
const int N=120;
int n;
int a[N];
void solve(){
read(n);
for(int i=1;i<=n;++i) read(a[i]);
int cnt1,cnt2,cnt3;
cnt1=cnt2=cnt3=0;
for(int i=1;i<=n;++i){
if(a[i]==1) cnt1++;
else if(a[i]==2) cnt2++;
else cnt3++;
}
if(n==1) cout<<"Win"<<endl;
else if(cnt1==0 && n<=2) cout<<"Lose"<<endl;
else if(cnt1 && !cnt2 && !cnt3){
if(cnt1%3==0) cout<<"Lose"<<endl;
else cout<<"Win"<<endl;
}
else if(cnt3==0){
if(((cnt1%3==1 || cnt1%3==2) && cnt2==2) || (cnt2==1)) cout<<"Win"<<endl;
else cout<<"Lose"<<endl;
}
else if(cnt3==1){
if(cnt2==1 && cnt1!=0){
if(cnt1%3==2 || cnt1%3==1)cout<<"Win"<<endl;
else cout<<"Lose"<<endl;
}
else if(cnt2==0 && cnt1!=0) cout<<"Win"<<endl;
else cout<<"Lose"<<endl;
}
else cout<<"Lose"<<endl;
}
signed main(){
//freopen(".in", "r", stdin);
//freopen(".out", "w", stdout);
read(T);
while(T--) solve();
return 0;
}
高二模拟赛
20251108
T1 颐气(captital)
题意

思路
显然正着做非常困难,考虑找到最少能删去的边权和。
自然是最小生成树,不过数据规模都是 \(1e5\) 的,若是建出这个图那就是 \(1e10\) 还带 \(\log\),肯定不行,考试的时候想到这里卡住了,因为显然是不能真的全跑一遍,而且这里面有很多边权一样的边,肯定是不用全算的。
所以问题的关键就是一类的多少条边是要删的,多少条要保留,Kruskal 的流程是从小边权的边开始找,然后看最少几条这种边可以把横着或竖着的所有边都连上。
比如一条横着的边,最开始如果它是边权最小的,肯定是所有竖点都要这条边是最优的,然后我们会发现这样选了以后,相当于剩下没有连在一起的横点减少了 \(1\),竖点类似,所以就能做了。
对竖点和横点要分开查并查集。
代码
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
#define PII pair<int, int>
#define mk(a, b) make_pair(a, b)
using namespace std;
template <typename P>
inline void read(P &x) {
P res = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
res = (res << 3) + (res << 1) + (ch ^ 48);
ch = getchar();
}
x = res * f;
}
template <typename Ty, typename... Args>
inline void read(Ty &x, Args &...args) { read(x); read(args...); }
int T = 1;
const int N = 1e5 + 10;
int n, m, p, q;
struct edge {
int u, v, w;
bool type;
bool operator < (const edge &b) const {
return w < b.w;
}
} e[N * 2];
int fa[2][N], tot = 0;
int find(int x, int k) { return fa[k][x] == x ? x : fa[k][x] = find(fa[k][x], k); }
inline void solve() {
read(n, m, p, q);
int sum = 0;
for (int i = 1; i <= n; ++i) fa[1][i] = i;
for (int i = 1; i <= m; ++i) fa[0][i] = i;
for (int i = 1; i <= p; ++i) {
++tot;
read(e[tot].u, e[tot].v, e[tot].w);
e[tot].type = 0;
sum += e[tot].w * n;
}
for (int i = 1; i <= q; ++i) {
++tot;
read(e[tot].u, e[tot].v, e[tot].w);
e[tot].type = 1;
sum += e[tot].w * m;
}
sort(e + 1, e + tot + 1);
int res = 0;
for (int i = 1; i <= tot; ++i) {
int u = e[i].u, v = e[i].v, w = e[i].w, f = e[i].type;
int ul = find(u, f), vl = find(v, f);
if (f == 0 && ul != vl) {
res += n * w;
m--;
fa[f][ul] = vl;
}
else if (f == 1 && ul != vl) {
res += m * w;
n--;
fa[f][ul] = vl;
}
}
printf("%lld\n", sum - res);
}
signed main() {
freopen("capital.in","r",stdin);
freopen("capital.out","w",stdout);
// read(T);
while (T--) solve();
return 0;
}
居然还是道紫题?%%%
T2 金科(rules)
链接是弱化版
题意

思路
这种选不选的问题(或者是选子序列),一般都是从 DP 入手,考虑 \(f_i\) 表示前 \(i\) 个训练营,第 \(i\) 个要选时的最小权值和,那么有:
其中 \(p\) 是在 \(i\) 之前的符合条件(红色线段不相交,黑色至少与红色交一次)的某条线段。
先离散化。
\(\mathcal{O}(n ^ 2)\) 非常容易,直接暴力枚举 \(i\) 之前的 \(p\) 点是哪个,然后直接转移。
\(\mathcal{O}(nlogn)\) 也比较显然,先用二分找到这条最靠右的满足条件的线段的左右端点,然后用 线段树 或者 ST表 维护 \(i\) 这一段 \(f_i\) 的最小值,然后转移即可,注意的是考试里这道题经过了加强,规模均为 \(5e6\),使用线段树会 \(TLE\),ST表 又容易 \(MLE\) (没错还卡空间,非常恶心),所以可能需要比较优秀的实现。原题 \(\mathcal{O}(nlogn)\) 且不用卡空间就可以通过
\(\mathcal{O}(n)\) 就比较困难了,首先下面那个 \(ST表\) 其实可以用单调队列维护最小值,这样就是线性的了,但是这时瓶颈却在排序和离散化,由于是对线段的结构体排序,故不能使用桶排这种东西了,可以使用基数排序,总之就是很麻烦,但是考试的题不会卡排序的瓶颈,所以可以不管这个了。
代码还是没用基数排序,瓶颈没卡排序和离散化
代码
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
#define PII pair<int, int>
#define mk(a, b) make_pair(a, b)
using namespace std;
template <typename P>
inline void read(P &x) {
P res = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
res = (res << 3) + (res << 1) + (ch ^ 48);
ch = getchar();
}
x = res * f;
}
template <typename Ty, typename... Args>
inline void read(Ty &x, Args &...args) { read(x); read(args...); }
int T = 1;
const int N = 5e6 + 10;
int n, m;
unsigned int seed;
struct line {
int l, r, w;
} a[N];
int b[N << 1], dp[N << 1];
int pos[N << 1], q[N << 1];
unsigned int rnd(unsigned int &x) {
x ^= (x << 13) & 0xFFFFFFF;
x ^= (x >> 17);
x ^= (x << 5) & 0xFFFFFFF;
x += 100;
return x;
}
inline void solve() {
read(n, m, seed);
for (int i = 1; i <= n; ++i) {
a[i].l = rnd(seed) & m;
a[i].r = rnd(seed) & m;
a[i].w = rnd(seed);
if (a[i].l > a[i].r) swap(a[i].l, a[i].r);
}
sort(a + 1, a + n + 1, [](const line &a, const line &b) {
return a.l < b.l;
});
for (int i = 1; i <= n; ++i) b[2 * i - 1] = a[i].l, b[2 * i] = a[i].r;
sort(b + 1, b + 2 * n + 1);
int len = unique(b + 1, b + 2 * n + 1) - b - 1;
for (int i = 1; i <= n; i++) {
a[i].l = lower_bound(b + 1, b + len + 1, a[i].l) - b;
a[i].r = lower_bound(b + 1, b + len + 1, a[i].r) - b;
}
for (int i = 1; i <= n; ++i) pos[a[i].r] = a[i].l;
int p = 1, pre = 0, ans = 0x3f3f3f3f3f3f3f3f;
int h = 0, t = 0;
memset(dp, 0x3f, sizeof(dp));
dp[0] = 0;
q[++t] = 0;
for (int i = 1; i <= n; ++i) {
while (p < a[i].l) {
pre = max(pre, pos[p]);
while (h <= t && dp[q[t]] >= dp[p]) t--;
q[++t] = p++;
}
while (h <= t && q[h] < pre) h++;
dp[a[i].r] = min(dp[a[i].r], dp[q[h]] + a[i].w);
if (a[i].r >= a[n].l) ans = min(ans, dp[a[i].r]);
}
printf("%lld\n", ans);
}
signed main() {
freopen("rules.in","r",stdin);
freopen("rules.out","w",stdout);
// read(T);
while (T--) solve();
return 0;
}
20251110
T1 调节关系(relationship)
题意

思路
由于 \(n \le 17\),考虑状压,发现一个满足条件的图必然是若干个朋友团和一些敌人边组成。
设 \(f_S\) 表示选择 \(S\) 中的奶牛,它们内部合法(即形成若干个团)的最少操作次数。为了帮助转移,再设一个 \(g_S\) 表示选择 \(S\) 的奶牛,它们内部要连成一个团的最少操作次数(这个可以 \(\mathcal{O}(n^22^n)\) 预处理)。那么有:
要枚举子集所以是 \(\mathcal{O}(n ^ 2 2 ^ n + 3 ^ n)\)。
原题里要变成补图
代码
#include <bits/stdc++.h>
#define endl '\n'
#define ll long long
#define PII pair<int, int>
#define mk(a, b) make_pair(a, b)
using namespace std;
template <typename P>
inline void read(P &x) {
P res = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
res = (res << 3) + (res << 1) + (ch ^ 48);
ch = getchar();
}
x = res * f;
}
template <typename Ty, typename... Args>
inline void read(Ty &x, Args &...args) { read(x); read(args...); }
int T = 1;
int n, m;
int mp[20][20];
int f[(1 << 19)], g[(1 << 19)];
inline void solve() {
read(n, m);
// for (int i = 1; i <= n; ++i) for (int j = 1; j <= n; ++j) mp[i][j] = 1;
for (int i = 1; i <= m; ++i) {
int x, y;
read(x, y);
mp[x][y] = mp[y][x] = 1;
}
for (int s = 0 ; s < (1 << n); ++s) {
for (int i= 1; i <= n; ++i) {
if ((s >> (i - 1)) & 1)
for (int j = 1; j <= n; ++j) {
if (i == j) continue;
g[s] += ((s >> (j - 1)) & 1) ? (!mp[i][j]) : mp[i][j];
}
}
}
for (int S = 0; S < (1 << n); ++S) {
f[S] = g[S];
for (int s = S; s; s = (S & (s - 1))) {
f[S] = min(f[S], f[S ^ s] + g[s]);
}
}
printf("%d\n", f[(1 << n) - 1] / 2);
}
signed main() {
freopen("relationship.in","r",stdin);
freopen("relationship.out","w",stdout);
// read(T);
while (T--) solve();
return 0;
}
T2
还不会,咕了
T3 流浪者的背包(knapsack)
题意

思路
这种要凑满多少多少然后求方案数的基本都可以从生成函数入手。
考虑每个 \(a_i\) 的数列是:
生成函数形式就是:
所以我们要求的就是:
由于 \(m \le 1e18\) 非常巨大,不可能直接多项式乘出来。所以用上一个科技
下面这个用 Bostan-mori 算法可以直接解决。

inline void Bostan_Mori(int N, Poly F, Poly G) {
int L = F.deg;
Poly H, A, B;
F.set(L << 1), G.set(L << 1), H.set(L << 1), A.set(L << 1), B.set(L << 1);
while (N) {
H = G;
for (int i = 1; i < L; i += 2) H[i] = mod - H[i];
F.NTT(L << 1, 1), G.NTT(L << 1, 1), H.NTT(L << 1, 1);
for (int i = 0; i < L << 1; ++i) A[i] = F[i] * H[i] % mod, B[i] = G[i] * H[i] % mod;
A.NTT(L << 1, 0), B.NTT(L << 1, 0);
for (int i = 0; i < L; ++i) B[i] = B[i * 2];
for (int i = 0; i < L; ++i) A[i] = A[2 * i + (N & 1)];
A.clear(L, (L << 1) - 1), B.clear(L, (L << 1) - 1);
F = A, G = B;
N >>= 1;
}
printf("%llu\n", F[0] * q_pow((int)G[0], mod - 2, mod) % mod);
}
代码还没写。。
20251117
考试前先上了个厕所,由于最近感冒了,所以考试的时候有点晕乎乎的,不过还能接受
开题后我先看了 T1、T2、T3,然后觉得 T2 比较有灵感,但是还是从 T1 开始写的,T1 感觉是一道贪心题,我先观察了一下样例发现没有什么启发性,然后看数据范围中存在对链的特殊考虑,然后发现如果是链的话比较好做,所以在没想出正解的情况下先把 T1 的特殊性质打满了,然后我发现了一些 T1 的性质但最终没能完全做出。
T2 是一个性质题,我上来发现一次询问 \((h, x, y)\) 必然是最底层的 \((x, y) \rightarrow (x + h, y + h)\) 所统御的,然后推出了一个错误结论:必须满足对角线全一样,且除此之外的其余部分与对角线颜色均不同。然后写了一些部分分,均通过了大样例,但是我发现大样例均很水,无法保证正确性,尝试构造小数据后感觉有点问题,所以先放了去看 T3。
T3 是排列计数题,考虑了一会儿发现有点困难放弃,回头看 T2,这时还剩余 \(40-50\) 分钟,我突然发现其实除对角线外的地方出现相同颜色其实是可以的,这时我又发现答案是否为 \(1\) 只跟对角线、对角线上下 \(2\) 条次对角线有关,于是先尝试了 \(\mathcal{O}(nQ)\) 的做法,发现其实细节很多,最后没有调出来。
下午看 solution 的时候发现我最后 T2 的方法居然是正解,可惜了。
T1 橡子 6(acorn)
题意

思路
如上所说,先把 \(w \ge h_u + h_v\) 和 \(w < \min\{h_u, h_v\}\) 的边去除,还有一类 \(w \ge \min\{h_u, h_v\} \wedge w < \max\{h_u, h_v\}\) 的边可以先把小的那个边选上,剩下的那个点保留,然后对剩下的边建图,对每个连通块,如果不为树或者存在一个点有连向外部(外部的点 \(v\) 即是刚刚删去的第三类边的小点)的边,答案就是这个连通块的大小,否则答案就是连通块大小减一。
代码
代码
#include <bits/stdc++.h>
#define endl '\n'
#define ll long long
#define PII pair<int, int>
#define mk(a, b) make_pair(a, b)
using namespace std;
template <typename P>
inline void read(P &x) {
P res = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
res = (res << 3) + (res << 1) + (ch ^ 48);
ch = getchar();
}
x = res * f;
}
template <typename Ty, typename... Args>
inline void read(Ty &x, Args &...args) { read(x); read(args...); }
int T = 1;
const int N = 1e6 + 10;
int n, m;
int a[N];
struct Edge{
int v, w, nex;
} G[N << 1];
int head[N], ecnt = 1;
void add(int u, int v, int w){
G[++ecnt] = Edge{v, w, head[u]};
head[u] = ecnt;
}
int siz = 0, cnt = 0;
bool f = 0;
bool vis[N], is[N], vise[N << 1];
void dfs(int u) {
siz++;
is[u] = 1;
for (int i = head[u]; i; i = G[i].nex) {
int v = G[i].v, w = G[i].w;
if (vis[v] && w >= a[u]) f = 1;
if (!is[v] && !vis[v]) dfs(v);
if (!vis[v] && !vise[i]) {
vise[i] = vise[i ^ 1] = 1;
cnt++;
}
}
}
int ans = 0;
inline void solve() {
read(n, m);
for (int i = 1; i <= n; ++i) read(a[i]);
for (int i = 1; i <= m; ++i) {
int u, v, w;
read(u, v, w);
u++, v++;
if (w >= a[u] + a[v]) {
ans += (!vis[u]) + (!vis[v]);
vis[u] = vis[v] = 1;
continue;
}
else if (w >= a[u] && w < a[v]) {
ans += (!vis[u]);
vis[u] = 1;
continue;
}
else if (w >= a[v] && w < a[u]) {
ans += (!vis[v]);
vis[v] = 1;
continue;
}
else if (w < min(a[u], a[v])) continue;
add(u, v, w), add(v, u, w);
}
for (int i = 1; i <= n; ++i) {
if (!vis[i] && !is[i]) {
f = 0, siz = 0, cnt = 0;
dfs(i);
if (cnt >= siz) ans += siz;
else if (f) ans += siz;
else ans += siz - 1;
}
}
cout << ans << endl;
}
signed main() {
freopen("acorn.in","r",stdin);
freopen("acorn.out","w",stdout);
// read(T);
while (T--) solve();
return 0;
}
T2 金字塔(pyramid)
题意
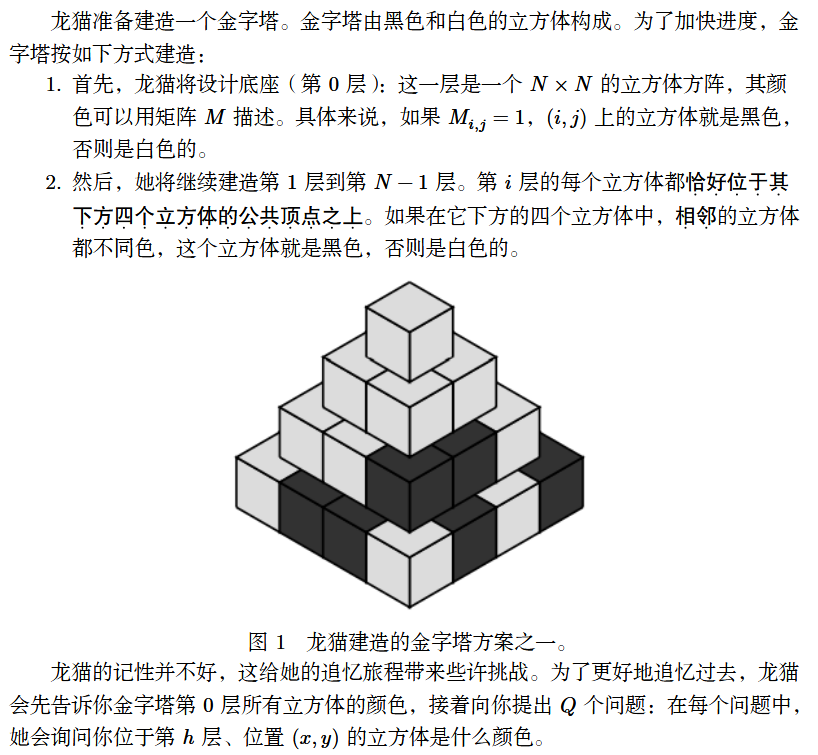

思路
仍然如上文总结所说,两种做法:
-
观察到一个重要的事实:一个底座,往上搭两层之后,仅仅会剩下若干形如“对角线”的黑色不交图形,这个可以暴搜所有小规模底座得出。于是先预处理底下三层(\(0,1,2\) 层),若查询更高的立方体颜色则判断它是否可以被一条第 \(2\) 层的对角线生成。
-
另一个可行的做法是,注意到对于一个大小为 \(n\) 的金字塔,塔尖答案为
1当且仅当底座有一条长度为 \(n\) 的对角线颜色相同,并且对角线周围的“阶梯”上的点颜色均与对角线不同:
abb?? ??bba
babb? ?bbab
bbabb or bbabb
?bbab babb?
??bba abb??
a ≠ b
代码
还没写完
20251118 CF 1064(Div.1)
A. Cyclic Merging
题意

思路
有点类似石子合并?每次合并肯定是从小代价开始比较好,所以我一开始想的是把相邻两个的 \(\max\) 放进小根堆然后每次拿出来再更新相邻关系,但是细节很麻烦,最后我还是考虑把每个元素直接丢进堆里然后每次取出来与前驱后继取 \(\max\) 来算答案。
至于前驱后继可以用数组模拟链表,实现还是比较好写的。
代码
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
#define PII pair<int, int>
#define mk(a, b) make_pair(a, b)
using namespace std;
template <typename P>
inline void read(P &x) {
P res = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
res = (res << 3) + (res << 1) + (ch ^ 48);
ch = getchar();
}
x = res * f;
}
template <typename Ty, typename... Args>
inline void read(Ty &x, Args &...args) { read(x); read(args...); }
int T = 1;
const int N = 2e5 + 5;
int n;
int a[N];
struct node {
int val, l, r;
bool flag;
};
priority_queue<PII, vector<PII>, greater<PII> > q;
inline void solve() {
read(n);
vector<node> v(n + 20);
for (int i = 0; i < n; ++i) read(a[i]);
if (n == 2) {
cout << max(a[1], a[0]) << endl;
return;
}
for (int i = 0; i < n; ++i) {
v[i].val = a[i];
v[i].l = (i - 1 + n) % n;
v[i].r = (i + 1) % n;
}
for (int i = 0; i < n; ++i) q.push(mk(a[i], i));
int ans = 0, siz = n;
while (siz > 1) {
auto [val, id] = q.top(); q.pop();
if (v[id].flag || v[id].val != val) continue;
auto [sum, pre, suf, vis] = v[id];
int p = (v[pre].val < v[suf].val) ? pre : suf;
int res = max(val, v[p].val);
v[id].val = res; v[p].flag = 1;
ans += res;
int pree = v[p].l, suff = v[p].r;
if (p == pre) v[id].l = pree, v[pree].r = id;
else v[id].r = suff, v[suff].l = id;
q.push(mk(res, id));
siz--;
}
while (!q.empty()) q.pop();
cout << ans << endl;
}
signed main() {
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
read(T);
while (T--) solve();
return 0;
}
B. Marble Council
题意

思路
首先每个 \(S\) 内的元素都代表了一个子序列。
设 \(c_i\) 为数 \(i\) 在 \(a\) 中的出现次数。先考虑这样一类 \(S\):若有 \(x \in S\),则 \(x\) 在 \(S\) 中的出现次数恰为 \(c_x\)。考察这样的 \(S\) 合法情况及其影响。
若 \(|S| \ge \max\{c_i\}\),那么可以对于每个 \(i \notin S\),将 \(c_i\) 个 \(i\) 分散在 \(c_i\) 个子序列内,这样 \(S\) 内的每个元素始终是众数之一。
假设有一个 \(T \sub S\) 并且 \(T\) 中数的种类和 \(S\) 相同,此时必然存在一个正整数 \(i\),它在 \(S\) 中的出现次数多于 \(T\)。那么从 \(S\) 到 \(T\) 的过程相当于合并了某两个 \(i\) 代表的子序列。由于合并后的子序列 \(i\) 依旧是出现次数最多的数之一,因此 \(T\) 依旧合法。
若 \(|S| < \max\{c_i\}\),那么存在至少一个 \(c_i\) 没办法将 \(c_i\) 个 \(i\) 分散在恰好 \(c_i\) 个子序列内,此时必然存在一个子序列内 \(i\) 出现了多于一次,于是这时的 \(S\) 自然不合法。
同样地考虑 \(T\),将两个子序列合并后,要么是这个新的子序列不合法,要么是原来的某个子序列仍旧不合法。
所以我们只要考虑所有满足上述特殊条件的 \(S\) 是否合法即可。对于一个合法的 \(S\),它对答案贡献了 \(\prod\limits_{i \in S}c_i\)。
于是问题就变成了:求 \(c\) 所有合法的子序列的乘积和,一个子序列合法当且仅当其内元素之和不小于 \(\max\{c_i\}\)。
直接背包。设 \(f_{i,j}\) 表示考虑了正整数 \(1 \sim i\),选出的数的元素之和为 \(j\) 的权值之和。容易得到:
答案即为 \(\sum\limits_{i = \max\{c_i\}}f_{n, i}\)。时间复杂度 \(\mathcal{O}(n^2)\)。
代码
#include <bits/stdc++.h>
#define endl '\n'
#define ll long long
#define PII pair<int, int>
#define mk(a, b) make_pair(a, b)
using namespace std;
template <typename P>
inline void read(P &x) {
P res = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
res = (res << 3) + (res << 1) + (ch ^ 48);
ch = getchar();
}
x = res * f;
}
template <typename Ty, typename... Args>
inline void read(Ty &x, Args &...args) { read(x); read(args...); }
int T = 1;
const int N = 5005;
const ll mod = 998244353;
int n;
int a[N], cnt[N];
ll f[N][N];
inline void solve() {
read(n);
memset(cnt, 0, sizeof(cnt));
int maxc = 0;
for (int i = 1; i <= n; ++i) read(a[i]), cnt[a[i]]++, maxc = max(maxc, cnt[a[i]]);
f[0][0] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = 0; j <= n; ++j) {
if (j < cnt[i]) { f[i][j] = f[i - 1][j]; continue; }
f[i][j] = (f[i - 1][j] + f[i - 1][j - cnt[i]] * cnt[i] % mod) % mod;
}
}
ll ans = 0;
for (int i = maxc; i <= n; ++i) ans = (ans + f[n][i]) % mod;
printf("%lld\n", ans);
}
signed main() {
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
read(T);
while (T--) solve();
return 0;
}
C. Binary Wine
题意

思路
首先由于 \(c \le 2^{30}\),而且我们每次选的数都至少要覆盖一个二进制位才是不劣的,所以我们最多选 \(30\) 个数就能得到 \(c\),其次当 \(a\) 越大的时候限制越松,所以肯定是优先考虑 \(a_i\) 越大的。
每次就只需要把 \(a_i\) 前 \(30\) 大的放进大根堆里,然后对 \(c\) 在二进制下从高位到低位扫一遍,如果是 \(1\),代表这一位是需要来一个数把它填上的,从堆里拿一个 \(a_i\) 出来与 \((1 << i)\) 比较,若大于,说明这一位不需要再填了,把 \(a_i - (1 << i)\) 重新放回堆里,否则说明需要进行变大操作,变大的次数即为差值 \((1 << i) - a_i\)。
代码
#include <bits/stdc++.h>
#define endl '\n'
#define ll long long
#define PII pair<int, int>
#define mk(a, b) make_pair(a, b)
using namespace std;
template <typename P>
inline void read(P &x) {
P res = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
res = (res << 3) + (res << 1) + (ch ^ 48);
ch = getchar();
}
x = res * f;
}
template <typename Ty, typename... Args>
inline void read(Ty &x, Args &...args) { read(x); read(args...); }
int T = 1;
const int N = 5e5 + 5;
int n, q;
int a[N];
inline void solve() {
read(n, q);
for (int i = 1; i <= n; ++i) read(a[i]);
sort(a + 1, a + n + 1, greater<int>());
while (q--) {
int x;
read(x);
priority_queue<int> q;
for (int i = 1; i <= min(30, n); ++i) q.push(a[i]);
while (q.size() < 30) q.push(0);
ll ans = 0;
for (int i = 30; ~i; --i) {
if (x >> i & 1 ^ 1) continue;
int tmp = q.top(); q.pop();
if (tmp >= (1 << i)) q.push(tmp - (1 << i));
else ans += (1 << i) - tmp;
}
printf("%lld\n", ans);
}
}
signed main() {
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
read(T);
while (T--) solve();
return 0;
}
20251125
一来先看的 T1 和 T2,然后 T1 很自然地想到了两个方向来贪心,后面写完后过了所有大样例,但是我突然发现贪心似乎有点假,真正的做法应该是递归爆算,最后因为一些细节问题没过。
T2 是一个限制很恶心的题,遇到这种题可以考虑判断合法的条件是什么,然后假设没有这个限制的话会怎样,这道题就是这样的,不过没想到。
T3 性质比较多,首先是度数必须为偶数,然后就是分每个连通块求答案,做成一个 dfs生成树然后考虑从剥子树的方式来求解。
T4 是数学问题,可以逐渐从暴力和特殊性质入手,暴力不说了,特殊性质就是这道题的入手点。
T1基于1的算术(add)
题意

思路
首先可能会想到贪心,但是问题在于不知晓贪完后的数字所需要的步数,然后数据范围是 \(n \le 10^{15}\),拆位后就是 \(15\),可以 \(2^{15}\) 暴力算。
具体的,每次分两种情况,第一种是减去正好比自己小的 \(111 \cdots\),第二种则是被刚好大于这个数的 \(111\cdots\) 减去。
减去后的值同样递归算即可。
代码
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
#define PII pair<int, int>
#define mk(a, b) make_pair(a, b)
using namespace std;
template <typename P>
inline void read(P &x) {
P res = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
res = (res << 3) + (res << 1) + (ch ^ 48);
ch = getchar();
}
x = res * f;
}
template <typename Ty, typename... Args>
inline void read(Ty &x, Args &...args) { read(x); read(args...); }
int T = 1;
int n;
vector<int> p;
int dfs(int x, int n) {
if (x < 0) return 0;
int ls = dfs(x - 1, (n % p[x])) + (n / p[x]) * (x + 1);
int rs = dfs(x - 1, abs(n % p[x] - p[x]) % p[x]) + (n / p[x] + (n % p[x] != 0)) * (x + 1);
return min(ls, rs);
}
inline void solve() {
read(n);
p.emplace_back(1);
for (int i = 1; i < 17; ++i) p.emplace_back(p.back() * 10 + 1);
cout << dfs(16, n) << endl;
}
signed main() {
freopen("add.in","r",stdin);
freopen("add.out","w",stdout);
// read(T);
while (T--) solve();
return 0;
}
T2 逃离(car)
题意

思路
从左往右标号,那么第 \(i\) 辆车通过桥的条件就是 \(\ge sum[i - 1] = \sum\limits_{k = 1}^{i - 1}(r_j - l_j)\),这个的含义就是这辆车前面所有车辆的长度和,注意这里是大于等于,所以没有追上它前面那辆车就通过时这个式子同样成立。
每辆车都需要满足上面的约束,才能保证保证最后一辆车离开桥时没有车辆重叠,进一步地,我们发现,如果后车追赶上了前车,那么它的速度将变的和前车相同,此时,后车和前车将同时到达上述条件约束的位置,在此过程中,后车发生了速度改变,但前车始终保持匀速!
所以我们求得的这个时间的答案其实是一个最大值!
有了这个关键性质,我们只需算出假定每辆车速度均不改变,第 \(i\) 辆车行驶 \((t - l_i + sum[i - 1])\) 的距离所需的时间并取最大值即可,因为上面的性质保证:如果一辆车因前面的车减速,那么这辆车算出来的答案一定是比前面的车的答案小,最大值不会在这里取到,取到最大值的车一定是一辆始终匀速前进的车。
我们用堆维护最大时间的车,每次取出来让其速度增加 \(k\),重复 \(m\) 次即可。
代码
#include <bits/stdc++.h>
#define endl '\n'
#define ll long long
#define PII pair<int, int>
#define mk(a, b) make_pair(a, b)
using namespace std;
template <typename P>
inline void read(P &x) {
P res = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
res = (res << 3) + (res << 1) + (ch ^ 48);
ch = getchar();
}
x = res * f;
}
template <typename Ty, typename... Args>
inline void read(Ty &x, Args &...args) { read(x); read(args...); }
int T = 1;
const int N = 3e5 + 5;
int n, t, m, k;
struct car {
int l, len, v, s;
double tim;
bool operator < (const car &b) const {
return tim < b.tim;
}
} a[N];
priority_queue<car> q;
bool cmp(car &a, car &b) { return a.l < b.l; }
inline void solve() {
read(n, t, m, k);
for (int i = 1; i <= n; ++i) read(a[i].l, a[i].len, a[i].v), a[i].len = a[i].len - a[i].l;
sort(a + 1, a + n + 1, cmp);
int sums = 0;
for (int i = 1; i <= n; ++i) {
a[i].s = t + sums - a[i].l; a[i].tim = a[i].s * 1.0 / a[i].v;
q.push(a[i]), sums += a[i].len;
}
while (m--) {
auto tmp = q.top();
q.pop();
tmp.v += k, tmp.tim = tmp.s * 1.0 / tmp.v;
q.push(tmp);
}
printf("%.3lf", q.top().tim);
}
signed main() {
freopen("car.in","r",stdin);
freopen("car.out","w",stdout);
// read(T);
while (T--) solve();
return 0;
}
T3 南斯拉夫(yugo)
题意

思路
题意转化之后就是一个图(不保证全联通),每次可以选择一条边的其中一个点进行 \(+1 \lor -1\) 的操作,问最后所有点权均为 \(0\) 的方案。
首先图显然是若干连通块,每个连通块内的边数必为偶数,不然不可能有解,其次每个点是否合法是受到周围的边选哪边的影响的,我们考虑做一个 dfs 生成树,对于一个节点,先定连向子节点的边。具体来说,如果子节点目前入度为奇数,就从该节点连向子节点。否则从子节点连向该节点自己。这样能满足除了根之外的每个节点。由于边数为偶数,根节点在其他节点满足情况下一定满足入度为偶数。
代码有点麻烦没写了。
T4 数数(count)
题意

思路
\(\mathcal{O}(n ^ 2)\) 很容易。
对于特殊性质,由于 \(p \le 7000\),所以 \(a_i \le 3500\),直接暴力枚举 \(a_i\) 和 \(a_j\) 的值然后判答案即可。
根据特殊性质的提示,我们考虑这个式子能不能把 \(i\) 和 \(j\) 分开,
设 \(x=a_i+1, y=a_j\) ,则:
由于 \(1 \leq a_i<\left\lfloor\frac{p}{2}\right\rfloor\) ,所以 \(1<x+y=a_i+1+a_j<p\) ,在两边同时乘上 \((x+y)\):
只需要依次枚举,用unordered_map维护所有的 \(x^3-x^2\) 和 \(-y^3-y^2\) ,即 \(\left(a_i+1\right)^3-\left(a_i+1\right)^2\) 和 \(-a_j^3-a_j^2\) 即可,实时计算新的一项与前面的数列项产生的数对个数。时间复杂度 \(\mathcal{O}(n)\) 。
代码
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
#define PII pair<int, int>
#define mk(a, b) make_pair(a, b)
using namespace std;
template <typename P>
inline void read(P &x) {
P res = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
res = (res << 3) + (res << 1) + (ch ^ 48);
ch = getchar();
}
x = res * f;
}
template <typename Ty, typename... Args>
inline void read(Ty &x, Args &...args) { read(x); read(args...); }
int T = 1;
const int N = 5e5 + 10;
int n, p;
int ans;
unordered_map<int, int> p1, p2;
inline void solve() {
read(n, p);
for (int i = 1; i <= n; ++i) {
int x;
read(x);
int a = (x + 1) * (x + 1) % p * x % p, b = (- x * x % p * (x + 1) % p + p) % p;
ans += p1[b] + p2[a];
p1[a]++, p2[b]++;
}
cout << ans << endl;
}
signed main() {
freopen("count.in","r",stdin);
freopen("count.out","w",stdout);
// read(T);
while (T--) solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号